Caratteristiche generali della risonanza

Si dice risonanza il fenomeno per cui un sistema oscillante è in grado di assorbire energia da una sorgente esterna in modo particolarmente efficiente solo ad una (o più) frequenze ben precise.

Esaminiamone le caratteristiche grazie ad un esempio:

• Sappiamo per esperienza che una piccola spinta ad un'altalena la fa oscillare ad una frequenza ben precisa, detta frequenza propria che dipende dalla lunghezza dell'altalena, ma non dai dettagli della forza somministrata durante la spinta (vedi frequenze proprie).
• Se anziché applicare la spinta una sola volta la ripetiamo periodicamente nel tempo possiamo studiare come l'altalena risponde al variare della frequenza della nostra spinta.
• Troveremo che, se la forza applicata dall'esterno ha una frequenza prossima alla frequenza propria dell'altalena, quest'ultima tende ad oscillare in modo sempre più ampio.
• Invece, per frequenze della forza esterna molto maggiori o molto minori della frequenza propria, la nostra spinta ostacola l'oscillazione.
• Concludiamo quindi che la frequenza naturale di oscillazione (o frequenza propria) è perciò anche la frequenza per cui una forza esterna trasferisce energia al sistema oscillante nel modo più efficiente.

Ogni sistema fisico caratterizzato da frequenze proprie di oscillazione può risuonare con una sorgente esterna.

Oscillatore singolo

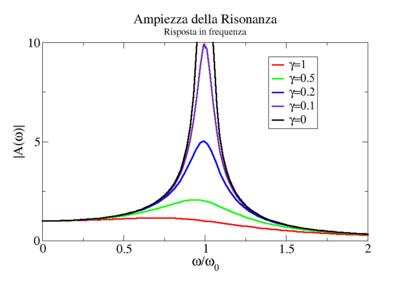
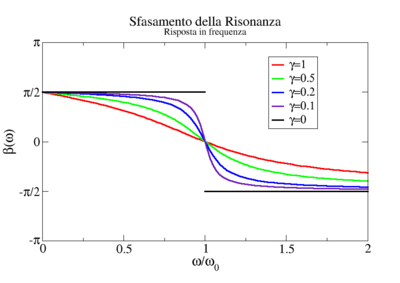
Anche se lo studio della risonanza dei sistemi reali può essere molto complicato, è semplice ed utile visualizzare alcune caratteristiche generali del fenomeno nel caso dell'oscillatore singolo. I dettagli del calcolo sono lasciati alle sezioni specifiche (vedi i collegamenti in fondo alla pagina), mentre qui riportiamo e commentiamo solo i due seguenti grafici.

• Studiamo un singolo oscillatore ideale (armonico) di frequenza propria ${\displaystyle \omega _{0}}$. Nei grafici, quindi, il punto in ascissa ${\displaystyle {\frac {\omega }{\omega _{0}}}=1}$ corrisponde al punto di risonanza.
• Nei grafici sono riportate più linee, ciascuna corrisponde ad un diverso valore del parametro ${\displaystyle \gamma }$, che rappresenta le forze di attrito presenti nel sistema: ${\displaystyle \gamma =0}$ significa che non c'è attrito; ad un ${\displaystyle \gamma }$ sempre più elevato corrispondono forze di attrito crescenti.
• NOTA: i grafici studiano la risposta in frequenza del sistema, e non i dettagli del suo moto. Il moto infatti può attraversare una fase transitoria prima di stabilizzarsi su un moto oscillante di data frequenza. Qui però non ci interessa la fase transitoria, e quindi i grafici si riferiscono all'ampiezza e alla fase del moto oscillatorio puro risultante dopo un certo tempo.
• NOTA: i grafici descrivono caratteri generali del fenomeno, mentre i dettagli numerici possono dipendere dal tipo di grandezze coinvolte. Per esempio: lo sfasamento assume valori differenti a seconda che si misuri l'ampiezza o la velocità (o la tensione e la corrente, nei sistemi elettrici) del moto risultante, ma le caratteristiche qualitative restano identiche nei due casi.

Ampiezza del moto oscillatorio al variare della frequenza della forza esterna	Sfasamento del moto oscillatorio al variare della frequenza della forza esterna
Si nota che l'ampiezza, partendo dal valore statico (a frequenza zero la forza esterna è una costante), cresce man mano che la frequenza si avvicina al valore in risonanza. Alla risonanza si raggiunge un valore massimo. Tanto maggiore quanto minore è l'attrito presente nel sistema. L'ampiezza decresce quando, oltrepassato il valore in risonanza, ce ne si allontana. Alle altissime frequenze l'ampiezza tende sempre a zero.	Si nota che lo sfasamento decresce man mano che la frequenza si avvicina al valore in risonanza. Per frequenze minori di quella di risonanza il moto avviene in ritardo (sfasamento positivo) rispetto alla forza. Alla risonanza si raggiunge sempre sfasamento zero indipendentemente dall'attrito presente nel sistema. Lo sfasamento diventa negativo quando, oltrepassato il valore in risonanza, ce ne si allontana. Ciò significa che il moto torna ad essere sfasato rispetto alla forza, ma in anticipo. In assenza di attrito si raggiunge un caso limite: lo sfasamento è sempre pari, in modulo, a 90°

massa variabile	costante elastica variabile
attrito variabile
	In queste animazioni si può osservare quale effetto si produce nella risposta in ampiezza di un oscillatore singolo se se ne modifica la massa, la costante elastica, e il coefficiente di attrito. Si osserva che un aumento della massa abbassa la frequenza di risonanza, mentre un aumento della costante elastica la innalza. L'attrito invece ha l'effetto di smorzare la risposta principalmente alla frequenza di risonanza (che si abbassa anche leggermente all'aumentare dell'attrito). I grafici sono in scala bilogaritmica, e recano, in ascissa, la frequenza f della forzante relativa alla frequenza f0 propria del sistema con ${\displaystyle m=1}$, ${\displaystyle k=1}$ e ${\displaystyle r=0.1}$. L'ordinata è proporzionale all'ampiezza massima ${\displaystyle X_{0}}$ dello spostameno. ${\displaystyle F_{0}}$ indica il massimo della forza esterna applicata

Sistemi di molti oscillatori

Una proprietà ugualmente generale dei sistemi oscillanti è la seguente: un sistema costituito da molti oscillatori accoppiati tra di loro possiede ancora risonanze, che però, in genere, non coincidono con quelle dei suoi componenti.

Esempio:

• Basta prendere un semplice sistema massa molla e collegarlo con un altro identico. I dettagli dei calcoli per questo sistema si trovano nella sezione oscillatori accoppiati. Qui basterà osservare che, mentre i due sistemi componenti hanno entrambi la stessa frequenza di risonanza ω₀, il sistema composto possiede due frequenze distinte: una identica a quella dei componenti ω₁=ω₀, mentre l'altra maggiore: ${\displaystyle \omega _{0}={\sqrt {3}}\omega _{0}}$.

Di conseguenza non basta semplicemente scomporre un sistema in sotto-sistemi oscillanti, per individuarne facilmente le risonanze, ma bisogna condurre una particolare analisi detta analisi modale, che è lo studio dei modi normali. Per i dettagli su questa procedure, e molti esempi si rimanda alle relative sezioni.

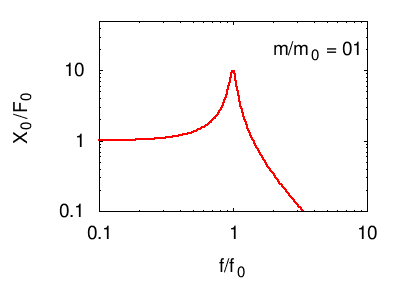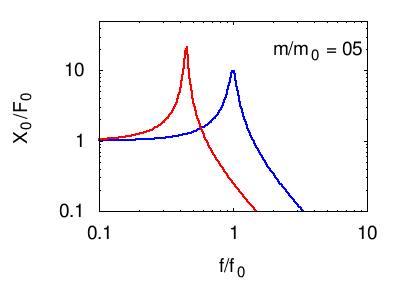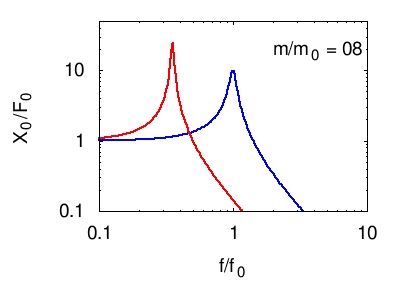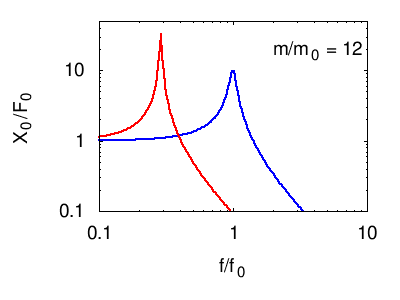
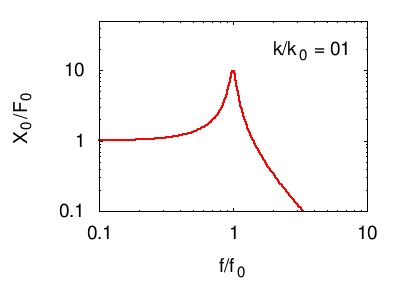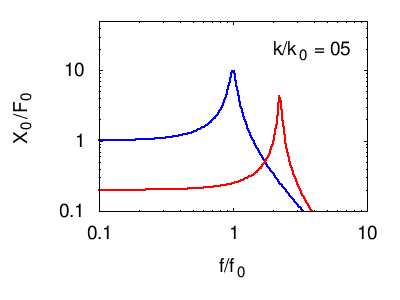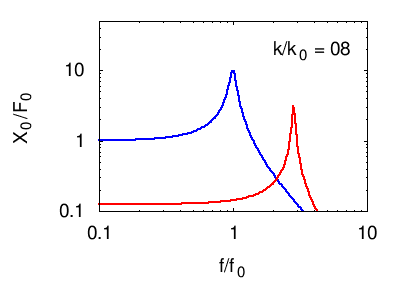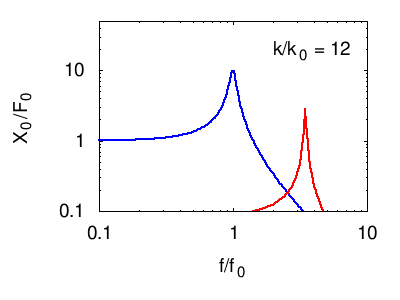
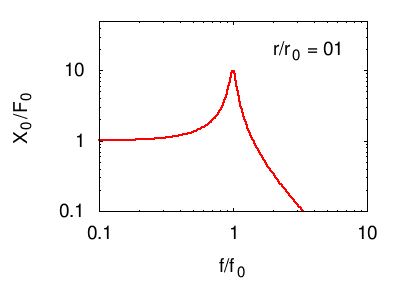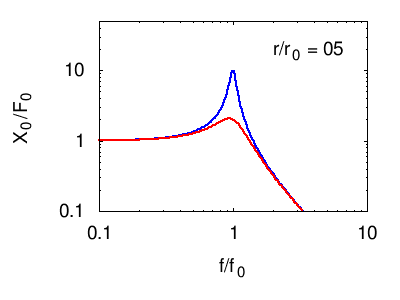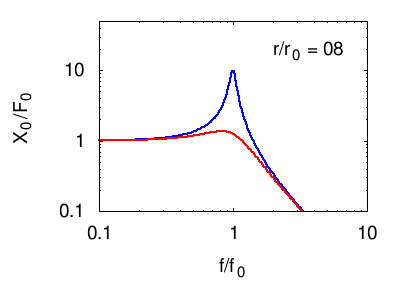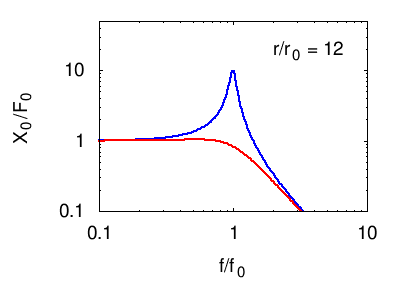
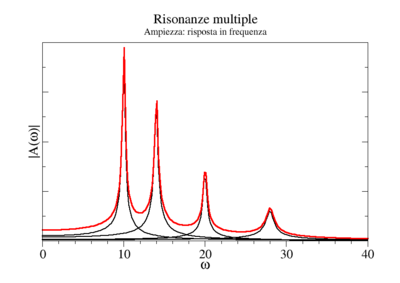
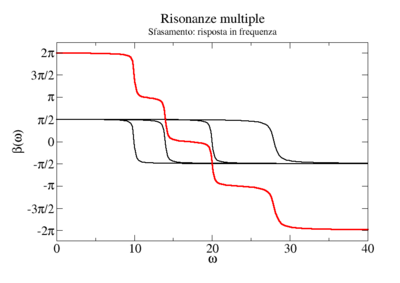
Nei grafici seguenti viene illustrata la risposta tipica di un sistema di più oscillatori. In ogni grafico vengono evidenziate, in nero, le risonanze elementari (dei modi normali) del sistema. La linea rossa è la somma di questi, e costituisce la risposta in frequenza complessiva del sistema.

Ampiezza al variare della frequenza della forza esterna	Sfasamento al variare della frequenza della forza esterna
I picchi di risonanza possono essere tutti diversi tra loro, cioè avere diversa frequenza di risonanza, ma anche diversa ampiezza e larghezza.	Lo sfasamento complessivo può non essere nullo in corrispondenza di ogni singola risonanza. In questo caso esso continua a decrescere all'aumentare della frequenza, ma, naturalmente, esistono casi più complessi.

Osservando posizione e larghezza dei picchi si possono dedurre le caratteristiche fisiche di ciascuno degli oscillatori normali del sistema (per vedere come consultare la pagina sull'impedenza). Tuttavia, questi parametri non corrispondono necessariamente ad alcuno dei sistemi che fisicamente compongono il sistema (vedi l'esempio citato nel paragrafo sistemi di molti oscillatori e alla pagina oscillatori accoppiati)

Esempi di fenomeni di risonanza

Fenomeni naturali

Il fenomeno della risonanza è fondamentale e universale. Caratterizza tutti i sistemi che abbiano le due proprietà necessarie per permettere le oscillazioni (corrispondenti ad inerzia ed elasticità nei sistemi meccanici), e lo si può osservare in moltissimi fenomeni naturali.

• Risonanza e maree
• Illusione acustica della conchiglia marina
• Emissione e assorbimento di luce in risonanza da parte degli atomi
• Pianeti e risonanze orbitali
• Risonanze nelle costruzioni: ponti, grattacieli e smorzatori sismici, motori

Sistemi fisici e dispositivi comuni

Il fenomeno della risonanza si può presentare anche in dispositivi e macchine costruite dall'uomo. Qui però dobbiamo distinguere due situazioni:

1. il fenomeno è desiderato, in quanto permette l'amplificazione o la selezione di un segnale. È il caso della radio, del laser, dei filtri. La risonanza permette di sintonizzare l'apparecchio, cioè di ottimizzarne la risposta in una o più bande di frequenze ben precise.
2. il fenomeno è indesiderato, in quanto il sistema in risonanza è soggetto a sollecitazioni che possono comprometterne l'integrità o il funzionamento. È il caso delle costruzioni (case, ponti, ecc.), in cui i materiali rischiano di deteriorarsi o rompersi, se sottoposti a sollecitazioni eccessive. La progettazione deve prevedere la possibilità di sollecitazioni in risonanza, e agire per desintonizzare la costruzione, smorzandone la risposta alle frequenze critiche.

In entrambi i casi la conoscenza del fenomeno ci permette di controllarlo, permettendo sia di favorire sia di inibire il comportamento risonante, a seconda del tipo di struttura. Nel seguito gli esempi sono catalogati a seconda del tipo di grandezze coinvolte. In ciascuna categoria si trovano esempi di risonanza "desiderata" e "indesiderata".

Acustici

• Risuonatori di Helmholtz
• Il corpo degli strumenti musicali
• Risonanza e acustica architettonica

Elettrici-elettronici

• Filtri passabanda
• Circuiti oscillanti e radio
• Il forno a microonde

Ottici

• Cavità Fabry-Pérot (etalon)

Magnetici

• La Risonanza magnetica nucleare

Dispositivi meno comuni

• Il FEL (Laser a elettroni liberi)
• L'ondulatore
• Il Klystron

Approfondimenti e collegamenti

I modi normali e la risonanza non sono fenomeni caratteristici solo dei sistemi elastici, ma sono comuni a tutti i sistemi oscillanti, siano essi elettrici, acustici, meccanici, macroscopici (cioè descritti dalla fisica classica) o quantistici (cioè descritti dalla fisica quantistica).

• Domande e risposte sulla risonanza
• Per una trattazione quantitativa della risonanza si faccia riferimento alle pagine che illustrano il concetto di impedenza, e, in particolare, impedenza dell'oscillatore armonico, impedenza di una corda vibrante, impedenza elettrica, impedenza acustica
• Per il calcolo delle frequenze di risonanza di diversi sistemi meccanici di particolare interesse per gli strumenti musicali si veda modi normali di una corda, modi normali di una membrana circolare, modi normali di una membrana rettangolare

---