Un semplice sistema di oscillatori armonici accoppiati

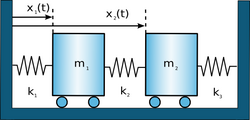
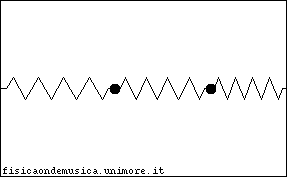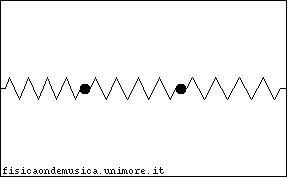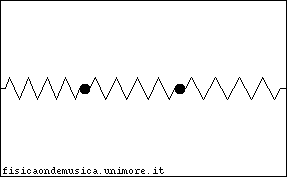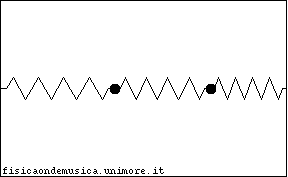
Immaginiamo di avere due sistemi massa-molla e di far interagire le masse tramite una terza molla (che genera una forza di tipo elastico) come nella figura a lato. Un sistema di questo tipo fornisce un esempio molto semplice di oscillatori accoppiati.

Nello studio di questo sistema assumeremo che:

• le masse siano puntiformi, cioè studieremo il loro moto senza preoccuparci della loro forma e dimensione; non consideriamo, ad esempio le loro rotazioni, o il loro ingombro;
• le forze siano di tipo elastico (dette anche Forze armoniche) cioè forze di richiamo proporzionali all'allungamento (o alla compressione) della molla rispetto alla posizione di riposo secondo una costante di proporzionalità negativa (detta costante elastica della molla);
• le oscillazioni siano longitudinali: le masse non potranno che oscillare in "orizzontale".

Perché studiamo questo sistema

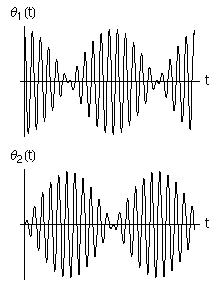
Il sistema fisico descritto, malgrado le numerose ipotesi che abbiamo introdotto e che introdurremo, per renderne più agevole lo studio, fornisce una sorprendente varietà di comportamenti rispetto al semplice oscillatore armonico. Infatti l'accoppiamento tra gli oscillatori permette loro di scambiarsi energia, ma la dinamica di questo scambio dipende da tutti i parametri del sistema, cioè da tutte le masse e le forze elastiche in gioco. Anche un accoppiamento relativamente debole può produrre trasferimenti di energia importanti. Nella figura a lato, per esempio è raffigurato il moto di due oscillatori quando la forza che li accoppia è 10 volte più debole della forza che fa oscillare ciascuno. Si nota un andamento delle oscillazioni identico a quello che in acustica provoca il fenomeno dei Battimenti. A turno ciascun pendolo smorza la propria oscillazione, mentre l'altro oscilla sempre più ampiamente, ma dopo un certo periodo i ruoli si invertono. Ciascuno dei due pendoli oscilla ad una frequenza molto vicina alla frequenza con cui oscillerebbe se fosse libero, mentre la frequenza di battimento è molto più lenta.

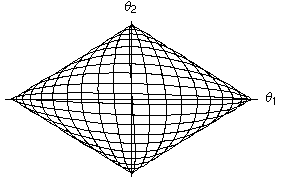
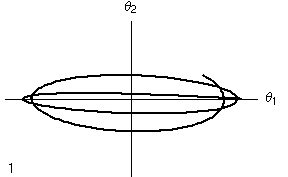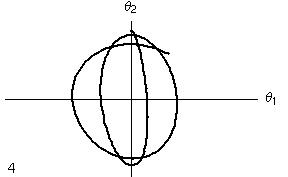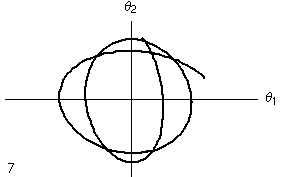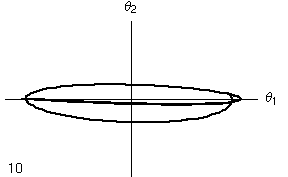
Utilizzando le Figure di Lissajous per l'analisi è possibile visualizzare l'andamento del moto in altro modo. In realtà, nella figura e animazione sottostanti è simulato solo un breve periodo di tempo. Come si scoprirà nel seguito, il rapporto tra i periodi dei due oscillatori non è razionale, il che significa che le curve di Lissajous sono destinate a ricoprire interamente l'area delimitata dal quadrilatero, lasciando evolvere il sistema per un tempo infinito. Nell'animazione si vede un rapido moto lungo la curva corrispondente all'oscillazione dei due pendoli, e un'alternanza più lenta, che sposta l'asse maggiore da orizzontale a verticale e viceversa. Questa alternanza corrisponde alla frequenza di battimento. Il sistema, in assenza di attrito mantiene la sua energia totale, e continua ad oscillare in questo modo all'infinito.

Figura di Lissajous per i primi 10 periodi di oscillazione

Vediamo alcune proprietà notevoli di questo sistema fisico.

1. Esso, rispetto al caso del singolo oscillatore, manifesta più di una frequenza di risonanza.
2. Il suo moto complessivo si può scomporre, in un senso che chiariremo, nella "somma" di più oscillazioni armoniche che coinvolgono l'intero sistema. Chiameremo tali oscillazioni i modi normali del sistema.
3. Esso fornisce il primo passo per studiare una catena di oscillatori nella quale le oscillazioni si propagano per formare un'onda.

modo non normale	modo normale 1 (ω1)	modo normale 2 (ω2)
Le animazioni qui a fianco rappresentano moti periodici, e quindi sono rappresentabili con un numero finito di fotogrammi. Tuttavia, come è spiegato nel testo, le loro frequenze non stanno in un rapporto razionale. Di conseguenza ogni sovrapposizione dei due modi normali produce un modo di vibrazione non periodico, e quindi non rappresentabile con un numero finito di fotogrammi.

Analisi del sistema

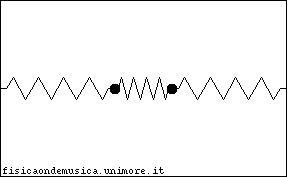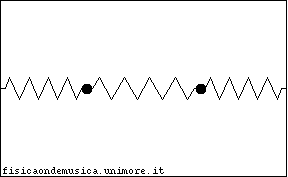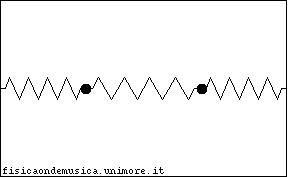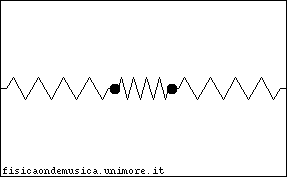
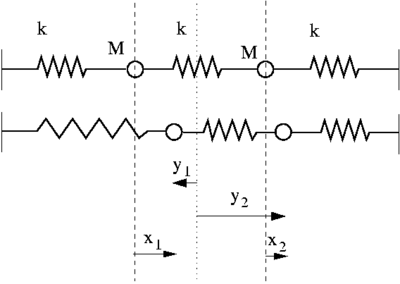
Consideriamo allora il sistema dei due oscillatori identici, costituiti da una massa M e da una molla di costante elastica k, collegati tramite una molla avente la stessa costante elastica k delle molle dei singoli oscillatori. Nella figura a lato si vede in alto il sistema nella configurazione "a riposo", e in basso il sistema in una possibile configurazione fuori dall'equilibrio "fotografata" ad un certo istante di tempo t. Chiameremo ${\displaystyle y_{1}}$ e ${\displaystyle y_{2}}$ la posizione delle masse M rispetto all'origine, mentre nel seguito utilizziamo le coordinate ${\displaystyle x_{1}}$ e ${\displaystyle x_{2}}$, che sono relative alla posizione di equilibrio di ciascuna massa (vedi figura).

Innanzitutto dobbiamo scrivere l'espressione della forza che si esercita su ciascuna massa M. Per ogni dato istante t essa è pari alla somma delle forze esercitate dalle due "molle" con cui essa interagisce. Dal sistema di riferimento in figura è facile ottenere

• per la massa a sinistra

${\displaystyle F_{1}=-kx_{1}+k(x_{2}-x_{1})\;}$

• per la massa a destra

${\displaystyle F_{2}=-k(x_{2}-x_{1})-kx_{2}\;}$

Dette ${\displaystyle a_{1},a_{2}}$ le accelerazioni rispettivamente della massa 1 e 2, e applicando il secondo principio della dinamica alle due masse otteniamo:

${\displaystyle {\begin{cases}Ma_{1}=-kx_{1}+k[x_{2}-x_{1}]&\\Ma_{2}=F_{2}=-k(x_{2}-x_{1})-kx_{2}\end{cases}}}$

(1)

Si osservi che è venuta meno la proporzionalità tra accelerazione e spostamento x(t): le due masse non si muovono quindi di moto armonico. L'armonicità del moto può venir in parte recuperata nel modo seguente: se si sommano e si sottaggono le due equazioni del sistema (1) si ottiene il sistema:

${\displaystyle {\begin{cases}M(a_{1}+a_{2})=-k(x_{1}+x_{2})&\\M(a_{1}-a_{2})=-3k(x_{1}-x_{2})\end{cases}}}$

(2)

Introducendo ora le nuove coordinate

${\displaystyle {\begin{cases}X_{1}=x_{1}+x_{2}&\\X_{2}=x_{1}-x_{2}\end{cases}}}$

(3)

ricordando, che l'accelerazione è la derivata seconda dello spazio, e denominando ${\displaystyle a_{n1},a_{n2}}$ l'accelerazione delle nuove coordinate, si ottiene

${\displaystyle {\begin{cases}a_{n1}={\ddot {X}}_{1}=a_{1}+a_{2}&\\a_{n2}={\ddot {X}}_{2}=a_{1}-a_{2}\end{cases}}}$

(4)

Il sistema (2) diventa allora

${\displaystyle {\begin{cases}a_{n1}=-{\frac {k}{M}}X_{1}&\\a_{n2}=-{\frac {3k}{M}}X_{2}\end{cases}}}$

(5)

Si osservi come ora le equazioni siano divenute disaccoppiate. Infatti, la prima equazione contiene solo variabili con indice 1, mentre la seconda solo variabili con indice 2. Questo significa che esse possono essere risolte indipendentemente, e non c'è più bisogno di risolvere un sistema.

Per questo motivo, le nuove coordinate ${\displaystyle X_{1},X_{2}}$ vengono dette coordinate normali. Ora osserviamo che le nuove equazioni "normali" definiscono il ben noto moto armonico, di cui già conosciamo la soluzione. Si ottiene allora

${\displaystyle X_{1}(t)=A_{1}\sin \left(\omega _{1}t+\phi _{1}\right)}$

(6)

${\displaystyle X_{2}(t)=A_{2}\sin \left(\omega _{2}t+\phi _{2}\right)}$

(6')

ove si è posto

${\displaystyle \omega _{1}={\sqrt {\frac {k}{M}}}{\mbox{ e }}\omega _{2}={\sqrt {\frac {3k}{M}}}}$

(7)

Ovviamento, ritornando alle coordinate ${\displaystyle x_{1}(t){\mbox{ e }}x_{2}(t)}$, dal sistema (3) si ottiene:

${\displaystyle x_{1}={\frac {1}{2}}(X_{1}+X_{2})}$,

(8)

${\displaystyle x_{2}={\frac {1}{2}}(X_{1}-X_{2})}$

(8')

dalle quali, sostituendo le (6) otteniamo infine

${\displaystyle x_{1}(t)={\frac {1}{2}}A_{1}\cdot \sin \left(\omega _{1}t+\phi _{1}\right)+{\frac {1}{2}}A_{2}\cdot \sin \left(\omega _{2}t+\phi _{2}\right)}$

(9)

${\displaystyle x_{2}(t)={\frac {1}{2}}A_{1}\cdot \sin \left(\omega _{1}t+\phi _{1}\right)-{\frac {1}{2}}A_{2}\cdot \sin \left(\omega _{2}t+\phi _{2}\right)}$

(9')

Le equazioni (9) e 9' rappresentano le infinite leggi orarie con cui possono muoversi le due masse: il sistema delle due masse selezionerà una sola di queste in modo da soddisfare determinate condizioni iniziali in cui si trova all'istante uguale t=0. Fissare le condizioni iniziali di tale sistema dinamico significa precisare:

• la posizione iniziale delle due masse (nel caso in esame il valore di ${\displaystyle x_{1}(0)}$ e ${\displaystyle x_{2}(0)}$)

• la velocità iniziale delle due masse (nel caso in esame il valore di ${\displaystyle v_{1}(0)}$ e ${\displaystyle v_{2}(0)}$)

	Il modo normale 1 si otterrà imponendo ${\displaystyle x_{1}(0)=x_{2}(0)=0\;}$ ${\displaystyle v_{1}(0)=v_{2}(0)=v_{0}\;}$ che equivale a spingere, partendo dalla posizione di riposo, le due masse nella stessa direzione con la medesima velocità iniziale.
	Il modo normale 2 si otterrà imponendo ${\displaystyle x_{1}(0)=x_{2}(0)=0\;}$ ${\displaystyle v_{1}(0)=-v_{2}(0)\;}$ che equivale a spingere, partendo dalla posizione di riposo, le due masse nella stessa in direzioni opposte la medesima velocità iniziale (in modulo)

È interessante osservare che qualunque condizione iniziali diversa dalle due precedenti genera un moto che è una "composizione" dei due moti normali; l'aspetto sorprendente della faccenda è tale moto non è periodico, cioè il sistema delle due masse, per quanto possiamo attendere non transiterà mai in una configurazione già visitata. Tale incredibile proprietà, tanto più incredibile se si pensa alla semplicità del sistema esaminato, deriva dalla non commensurabilità delle frequenze dei due modi normali (cioè dalla impossibilità di esprimere il loro rapporto tramite un numero razionale). Si ha infatti:

${\displaystyle {\frac {\omega _{2}}{\omega _{1}}}={\sqrt {3}}}$

(10)

Approfondimenti e collegamenti

• Nella pagina relativa ai modi normali scoprirai che la possibilità di esprimere oscillazioni complicate come sovrapposizione di modi più semplici non è limitata al semplice sistema che abbiamo descritto in questo pagina ma è una procedura generale applicabile ad ogni sistema vibrante;

• Nella pagina relativa alla risonanza scoprirai che il valore delle frequenze dei modi normali determina in modo decisivo le modalità con cui un sistema vibrante può ricevere o cedere energia dall'esterno;

• Pur nella sua semplicità il sistema dei due oscillatori accoppiati descritti in questa pagina può servire da paradigma per sistemi di oscillatori più complicati. Essi possono essere ad esempio
  • un edificio e il basamento su cui esso poggia che in caso di terremoto viene messo in oscillazione trasferendo parte del suo moto all'edificio stesso (visita, per approfondire la pagina Risonanza negli edifici).
  • una corda di violino e la cassa armonica del violino stesso (visita, per approfondire, la sezione violino e suono e risonanza).

---