Che cos'è una catena di oscillatori

Una catena di oscillatori è semplicemente un insieme di masse puntiformi allineate e interagenti tra loro per mezzo di forze armoniche.

• Masse puntiformi vuol dire che studiamo il moto delle masse senza preoccuparci della loro forma e dimensione. Non consideriamo, ad esempio le loro rotazioni, o il loro ingombro.
• Forze armoniche sono forze che obbediscono ad una semplice legge: la forza che si esercita tra due punti è direttamente proporzionale alla distanza tra di essi.

Per esempio, detta ${\displaystyle x_{1}}$ la posizione del punto 1, e ${\displaystyle x_{2}}$ la posizione del punto 2, l'espressione di una forza armonica che il punto 2 esercita sul punto 1 può essere

${\displaystyle F_{21}=-k(x_{1}-x_{2})\!}$

Osserviamo che:

1. La forza può essere sia attrattiva sia repulsiva: se ${\displaystyle k>0}$ le due masse si attraggono. Infatti si vede che la forza sulla particella 1 è diretta sempre verso la particella 2.
2. Se ${\displaystyle x_{1}=x_{2}}$ la forza è nulla. Quindi la posizione di equilibrio si raggiunge quando le masse sono a contatto. Ovviamente due masse reali non possono occupare la stessa posizione, mentre il problema non sussiste per due masse puntiformi.

Un'altra espressione per la forza armonica è

${\displaystyle F_{21}=-k(x_{1}-x_{2}-d)\!}$.

In questo caso ${\displaystyle d>0}$ è una lunghezza che sposta la posizione di equilibrio delle masse. Infatti, in questo caso, si ha che la forza tra le due masse è nulla non quando le masse si trovano a contatto, ma quando si trovano a distanza d

${\displaystyle x_{1}-x_{2}=d\!}$.

Per esempio, se pensiamo alla forza armonica come alla forza esercitata da una molla ideale, questa seconda espressione è più utile, perché tiene conto del fatto che la molla ha una sua lunghezza finita all'equilibrio. d, appunto.

Perché studiamo questo sistema

Il sistema fisico che studiamo qui è solo apparentemente esotico. Vi sono molte ottime ragioni per cui vogliamo studiarne i segreti.

1. Innanzitutto è un sistema semplice, rispetto alle strutture meccaniche oscillanti quali ponti, case, motori, strumenti musicali, cristalli, ecc., e questa, per i fisici è già una buona ragione.
2. La forza armonica è un'eccellente approssimazione delle forze elastiche "vere", almeno finché le deformazioni in gioco sono piccole.
3. La forza armonica approssima anche altri tipi di forze non elastiche, quali le interazioni tra gli atomi, in certe particolari condizioni.
4. Se otteniamo un'equazione delle onde, potremo trasferire tutte le proprietà delle onde al nuovo sistema, senza curarci troppo dei dettagli della sua struttura.
5. La catena è un sistema discreto, e non continuo. Questo significa che ha un numero finito di componenti, e quindi che essa può essere calcolata su un computer. In altre parole mentre l'equazione delle onde per i sistemi continui deve essere discretizzata per poter essere risolta numericamente in una macchina, questa equazione può essere utilizzata direttamente. Per un esempio di implementazione vedi il paragrafo sulla simulazione numerica.

L'ultimo punto ha una grandissima importanza per due motivi:

1. La simulazione numerica delle oscillazioni e delle onde nei sistemi continui si riduce sempre, in ultima analisi, al calcolo di un sistema discreto.
2. La struttura della materia su piccola scala è in realtà discreta, perché essa si compone di atomi, e quanti.

Ricaviamo l'equazione

Consideriamo una catena di N oscillatori tutti uguali e disposti lungo una linea. Ogni oscillatore è costituito da una massa m, interagente con le le masse vicine mediante una forza elastica di costante k. Supponiamo che la distanza di equilibrio sia d, cioè che la forza elastica tra due masse sia nulla quando esse si trovano ad una distanza d. Nella figura a lato si vede in alto una parte della configurazione "a riposo", e in basso la catena in moto. Non siamo tanto interessati a conoscere le posizioni x(t) degli oscillatori in moto, quanto piuttosto il loro spostamento ${\displaystyle \xi (x,t)}$ dalle rispettive posizioni di equilibrio. Ci accorgiamo infatti che questa catena può essere attraversata da onde longitudinali di spostamento. La grandezza che si propaga lungo la catena è appunto lo spostamento ${\displaystyle \xi }$, mentre le masse finiranno per oscillare attorno alla loro posizione di equilibrio.

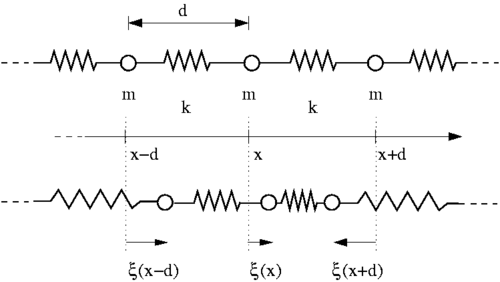
• Innanzitutto dobbiamo scrivere l'espressione della forza che si esercita sulla massa situata alla posizione x. Per ogni dato istante t essa è pari alla somma delle forze esercitate dalle due "molle" con cui essa interagisce

${\displaystyle F(x+d)+F(x-d)=dF(x)=k\left[\xi (x+d)-\xi (x)\right]+k\left[\xi (x-d)-\xi (x)\right]}$

• L'equazione del moto per la massa collocata nel punto x è

${\displaystyle dF(x,t)=ma(x,t)=m{\frac {d^{2}}{dt^{2}}}x(t)=m{\frac {\partial ^{2}}{\partial t^{2}}}{\xi (x,t)}}$

• Eguagliando i due termini si trova

${\displaystyle k[\xi (x+d,t)-\xi (x,t)-\xi (x,t)+\xi (x-d,t)]=m{\frac {\partial ^{2}}{\partial t^{2}}}\xi (x,t)}$

• Ora possiamo introdurre le grandezze caratteristiche della catena, anziché di una sola delle masse componenti, e, in particolare, diciamo ${\displaystyle L=Nd}$ la lunghezza della catena, ${\displaystyle M=Nm}$ la sua massa, e ${\displaystyle K=k/N}$ la costante sua rigidità.

${\displaystyle {\frac {\partial ^{2}\xi (x,t)}{\partial t^{2}}}={\frac {KL^{2}}{M}}{\frac {\xi (x+d,t)-2\xi (x,t)+\xi (x-d,t)}{d^{2}}}}$

Un caso limite: dalla catena discreta alla corda continua

Il caso limite in cui in una lunghezza finita L sono concentrate tantissime masse è molto importante. Esso corrisponde a considerare il sistema come un continuo, anziché un insieme discreto di oscillatori. In breve stiamo passando da una visione microscopica di una oggetto alla sua visione macroscopica. L'oggetto in questione diventa quindi una corda elastica. Se abbiamo fatto bene i nostri conti, l'equazione per il sistema di oscillatori si deve ridurre a quella per la corda.

Matematicamente addensare i punti significa ridurre h ed aumentare N in modo che il L e M rimangano costanti. Quindi dobbiamo calcolare il limite dell'equazione degli oscillatori per

${\displaystyle N\rightarrow \infty ,h\rightarrow 0}$.

Otteniamo

${\displaystyle {\frac {\partial ^{2}\xi (x,t)}{\partial t^{2}}}={\frac {KL^{2}}{M}}{\frac {\partial ^{2}\xi (x,t)}{\partial x^{2}}}}$,

e vediamo subito che il rapporto ${\displaystyle {\frac {KL^{2}}{M}}}$ corrisponde al quadrato della velocità di propagazione delle onde nel mezzo continuo (la corda). Poiché ${\displaystyle {\frac {M}{L}}=\rho }$ è la sua densità (la massa per unità di lunghezza), troviamo facilmente due espressioni equivalenti per la velocità

la prima contiene solo grandezze macroscopiche

${\displaystyle c^{2}={\frac {KL^{2}}{M}}={\frac {T}{\rho }}}$.

dove ${\displaystyle T=KL\!}$ ha le dimensioni di una forza (e corrisponde alla tensione della corda). La seconda espressione contiene solo grandezze microscopiche

${\displaystyle c^{2}={\frac {kd^{2}}{m}}}$,

e lega le proprietà microscopiche k, d ed m del singolo oscillatore alla velocità delle onde nel mezzo macroscopico.

NOTA: abbiamo anche ottenuto una regola che ci indica come approssimare una derivata seconda nel continuo con una semplice somma di termini nel discreto

${\displaystyle {\frac {\partial ^{2}\xi (x,t)}{\partial x^{2}}}\to {\frac {\xi (x+d,t)-2\xi (x,t)+\xi (x-d,t)}{d^{2}}}}$

Questa espressione è della massima utilità nel paragrafo che segue.

Alla pagina sulla catena di Fermi-Pasta-Ulam si trova un programma Matlab che risolve l'equazione delle onde per una catena di oscillatori anche in presenza di forze non armoniche.

---