Equazione delle onde nella corda
Da "Fisica, onde Musica": un sito web su fisica delle onde e del suono, acustica degli strumenti musicali, scale musicali, armonia e musica.
Jump to navigation Jump to searchL'equazione ordinaria
Consideriamo una corda ideale di lunghezza L, disposta lungo l'asse x e libera di oscillare trasversalmente nella direzione y. L'equazione lineare delle oscillazioni è
- ,
dove è la densità lineare della corda, e la sua tensione.
Questa equazione altro non è che la comune equazione del moto di Newton
- ,
solo che è specializzata per un sistema continuo quale è la corda.
Come si ricava
L'equazione si ricava nel seguente modo:
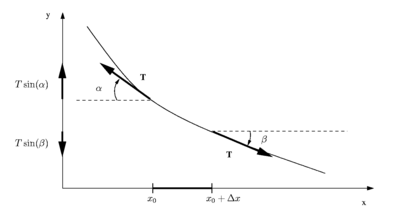
- consideriamo un tratto infinitesimo della corda mentre essa è in oscillazione. Diciamo dx la sua lunghezza. La sua massa di conseguenza è .
- Per questo piccolo tratto vogliamo scrivere l'equazione del moto nella direzione perpendicolare alla lunghezza della corda: .
- Il bilancio delle forze è semplice perché vi è solo la forza di tensione che agisce agli estremi del piccolo tratto considerato. Le particolari ipotesi che rendono la corda ideale hanno infatti queste conseguenze:
- T è costante durante il moto della corda (cioè qualunque sia la sua deformazione)
- T ha la stessa intensità lungo tutta la corda, e, in ogni punto, agisce solo nella direzione tangente la corda (cioè senza componenti perpendicolari alla corda).
- tutte le altre forze esterne (come la forza di gravità) sono trascurate rispetto a T.
- Il moto della corda è solo trasversale, perciò l'accelerazione della corda è solo lungo l'asse y. Il secondo membro dell'equazione di Newton (massa per accelerazione) si scrive allora
Eguagliando i due membri sopra ottenuti si ottiene l'equazione del moto citata all'inizio.
Va bene, ma cosa significa?
|
Con una semplice analisi dimensionale ci si accorge che il termine
ha le dimensioni del quadrato di una velocità. Infatti, scrivendo l'equazione delle onde nella corda come
si vede che i numeratori hanno le stesse dimensioni, e il denominatore di sinistra ha le dimensioni del quadrato di una lunghezza; pertanto il denominatore di destra deve avere anch'esso dimensioni pari al quadrato di una lunghezza. La costante c è importante perché è proprio la velocità con cui le onde si propagano nella corda. Nel nostro caso ideale è la velocità con cui tutte le onde si propagano nella corda. Lo si dimostra osservando che qualunque funzione della forma
dove e sono funzioni arbitrarie, è soluzione della nostra equazione delle onde. Ma altro non è che una che si sposta nel tempo ad una velocità costante c. Come si risolve
Corde "meno ideali"Nelle corde reali l'equazione delle onde non ha più in generale la forma descritta sopra. Vediamo come essa cambia se rinunciamo, una alla volta, alle ipotesi che abbiamo assunto per il caso ideale. Eliminiamo l'ipotesi n. 1T è costante durante il moto della corda (cioè qualunque sia la sua deformazione) Nelle corde reali accade che la tensione T dipenda dalla forma della corda stessa, o, almeno dallo spostamento massimo della corda dalla posizione di equilibrio. L'ipotesi n.1 è quasi sempre valida finché lo spostamento massimo della corda non è molto grande. In termini matematici eliminare questa ipotesi ideale consiste nel rendere T funzione di (più in generale funzionale di y(x))
Di conseguenza, facendo a meno dell'ipotesi ideale n. 1, la velocità delle onde nella corda non è più una costante, ma dipende dalla forma della corda stessa, o, almeno, dall'entità della sua deformazione.
Questo implica che per grandi spostamenti le onde viaggiano a velocità diversa che per piccoli spostamenti.
In questo caso velocità di fase e velocità di gruppo per le onde nella corda differiscono. Ovvero, onde di alta frequenza si propagano con velocità diversa rispetto ad onde di bassa frequenza. (Ricordiamo che, nel caso di onde sonore, frequenze più alte corrispondono generalmente a suoni più acuti) Eliminiamo l'ipotesi n.2Parte prima: T ha la stessa intensità lungo tutta la corda... Questa ipotesi è in realtà piuttosto ben giustificata se la corda è omogenea. Il caso di corde non omogenee non è di particolare interesse per gli strumenti musicali, o per le oscillazioni, mentre trova importanti applicazioni nella trasmissione di segnali nelle linee elettriche, e nella trasduzione, (vedi per esempio impedenza, riflessione nelle corde, rifrazione nelle corde). Parte seconda:...in ogni punto, agisce solo nella direzione tangente la corda (cioè senza componenti perpendicolari alla corda). Considerare componenti trasversali della tensione nella corda significa pensare alla corda non più come un sistema unidimensionale, ma come un vero e proprio sistema tridimensionale. Si pensi, per esempio, anziché ad una corda di violino, ad un grosso cavo d'acciaio per un ponte sospeso. Allora non potremo trascurarne, ad esempio, il moto di torsione, che può sottrarre energia ai modi di vibrazione trasversali, modificandoli. Si veda la sezione sulle onde nelle barre Eliminiamo l'ipotesi n. 3tutte le altre forze esterne (come la forza di gravità) sono trascurate rispetto a T. Se includiamo nell'equazione altre forze, allora il comportamento della corda dipende dalla natura di queste forze. In particolare è immediato introdurre forze di attrito che tendano a smorzare le oscillazioni, ed anche forze esterne che mantengano in vibrazione la corda contrastando l'attrito. Questi termini possono essere inclusi facilmente nell'equazione delle onde mantenendone il carattere lineare (p. es. sappiamo che il termine d'attrito conduce all'equazione telegrafica: v. equazione delle onde).
Per le onde descritte da un'equazione non lineare, non vale più il principio di sovrapposizione: due onde che si "scontrano" lungo questa corda si possono influenzare a vicenda! In questo regine si osserva una interessante varietà di fenomeni, alcuni dei quali, anche se non specifici delle corde, sono esaminati nelle pagine Effetti non lineari, Catena di Fermi-Pasta-Ulam, Distorsione di intermodulazione e Instabilità modulazionale |