Che cos'è

In matematica

È una importante proprietà algebrica dei sistemi di equazioni lineari: se esistono più soluzioni, ogni combinazione lineare di queste soluzioni è ancora una soluzione del sistema. Cioè: le soluzioni di un sistema lineare si possono moltiplicare per costanti arbitrarie, e sommare algebricamente tra loro, e ciò che si ottieme è ancora una soluzione dello stesso sistema.

In fisica

Lo stesso principio si applica a tutti i sistemi fisici che si possono descrivere tramite (sistemi di) equazioni lineari. In genere le "equazioni" in questione sono le equazioni dinamiche del sistema (p. es. le equazioni del moto), e le "soluzioni" sono le possibili evoluzioni temporali del sistema (per esempio i moti possibili).

Più formalmente possiamo dire che in tutte le situazioni in cui le grandezze fisiche di un sistema sono descritte da funzioni del tempo e della posizione f(r,t), soluzioni di equazioni differenziali lineari. Tali equazioni hanno la formidabile proprietà che se due funzioni f₁(r,t) e f₂(r,t) sono soluzioni dell'equazione differenziale anche una loro combinazione lineare, cioè una funzione del tipo

${\displaystyle \lambda f_{1}(\mathbf {r} ,t)+\mu f_{1}(\mathbf {r} ,t)}$ con ${\displaystyle \lambda ,\mu \in \mathbb {R} }$

Esempi e applicazioni

• Il principio di sovrapposizione ci dice, ad esempio, che, noti due moti semplici per un sistema lineare, è possibile combinarli per ottenere moti più complessi ugualmente leciti. Per "moto" qui si intende :
  • un vero e proprio movimento, come un'oscillazione, o una traslazione per un sistema meccanico;
  • in un sistema elettrico potrebbe essere il valore di una corrente che attraversa un dato elemento del circuito;
  • in un sistema acustico potrebbe essere il valore locale della pressione rispetto al valore di riferimento della pressione atmosferica; ecc.
• Viceversa, dato un moto complesso, si può cercare di esprimerlo come combinazione di moti elementari. Questo argomento è approfondito nelle sezioni modi normali, teorema di Fourier e sintesi delle onde.
  • P. es. queste animazioni illustrano come una semplice combinazione lineare di due oscillazioni semplici in una corda generi un'oscillazione più complessa (si veda anche la sezione sui modi normali di una corda).

=+

• Applicato alle onde il principio di sovrapposizione illustra il fatto che, in ogni punto dello spazio in cui due onde incidono simultaneamente, l'oscillazione complessiva è data dalla somma algebrica delle oscillazioni delle due onde incidenti prese separatamente.
  • Questa proprietà, comune a molti tipi di onde, almeno nel regime in cui esse non sono troppo intense, rende conto, ad esempio dell'esperienza per cui si possono udire più suoni simultaneamente: il suono complessivo è il risultato della sovrapposizione lineare dei singoli suoni.
  • Le onde generano figure complesse nelle regioni dello spazio in cui si trovano ad incidere simultaneamente, ma, apparentemente si "ignorano" a vicenda, emergendo da queste zone esattamente come vi erano entrate (vedi animazione qui sotto).

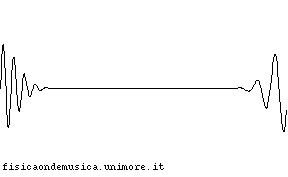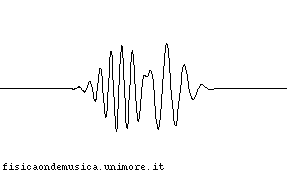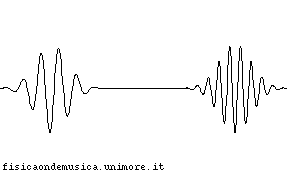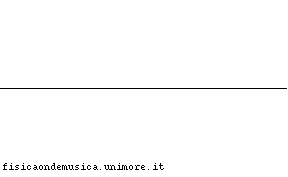
Perché è così importante

Il principio di sovrapposizione vale rigorosamente esclusivamente per i sistemi regolati da leggi fisiche lineari. Ovviamente in natura esistono anche sistemi non lineari (anzi essi sono la maggior parte, e mostrano una grande varietà di comportamenti interessanti). Allora perché il principio di sovrapposizione continua ad essere così utile?

1. L'algebra lineare è un campo molto ben conosciuto della matematica, ed esiste un vasto insieme di teoremi e tecniche che è possibile impiegare anche nello studio dei sistemi fisici, sia classici, sia quantistici.
   • Es.: dato un circuito elettrico, il principio di sovrapposizione ci permette di scomporlo in circuiti più semplici, e, una volta risolti questi ultimi, di ricomporre le soluzioni per ottenere quella del circuito iniziale.
   • Es.: lo stato di un atomo o di una molecola, per quanto complessa sia la sua evoluzione temporale, può sempre essere descritto in meccanica quantistica come una sovrapposizione di (infiniti) stati stazionari, cioè invarianti nel tempo.
2. È quindi evidente che, anche in presenza di sistemi non lineari, uno dei primi approcci consista spesso nella "linearizzazione" delle equazioni, cioè nel cercare un'approssimazione lineare alle equazioni del moto che renda possibile applicare le molte tecniche dell'algebra lineare.
   • Da un punto di vista fisico le equazioni linearizzate forniscono una descrizione approssimata "al prim'ordine" per tutti quei sistemi (e sono la gran parte) per cui a "piccole cause corrispondono piccoli effetti", cioè "ad una piccola sollecitazione esterna corrisponde una piccola risposta del sistema". Ad esempio la linearizzazione di una oscillazione produce un'equazione particolarmente semplice, la cui soluzione è nota come moto armonico.
   • In tutti i casi in cui si sostituisca allo studio di un sistema il suo modello lineare è molto importante definire bene entro quali parametri il modello descrive bene il sistema. Riferendoci al punto precedente, potremo senz'altro dire che, molto spesso, il sistema si discosta dal modello non appena le sollecitazioni non sono più "piccole", ma altre volte le non-linearità hanno un comportamento più subdolo.

Approfondimenti

• Condizioni di applicabilità del principio di sovrapposizione: le onde si possono sempre sovrapporre? Vedi equazione d'onda
• Il principio di sovrapposizione all'opera nell'interferenza, nel funzionamento delle antenne, e nella formazione di onde complesse
• Il principio di sovrapposizione nell'analisi dei segnali complessi: modi normali
• Il principio di sovrapposizione nella sintesi di segnali complessi: teorema di Fourier

---