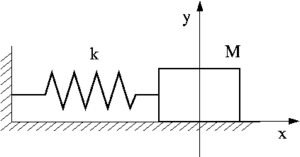
Moto armonico
Da "Fisica, onde Musica": un sito web su fisica delle onde e del suono, acustica degli strumenti musicali, scale musicali, armonia e musica.
Jump to navigation Jump to searchDefinizione e principali proprietà
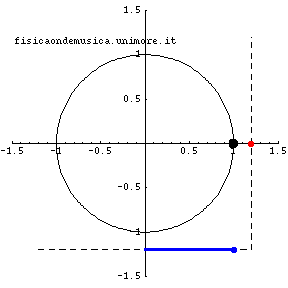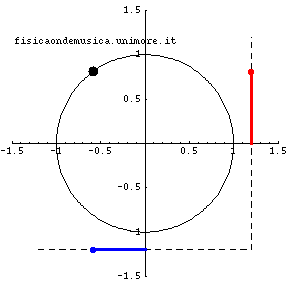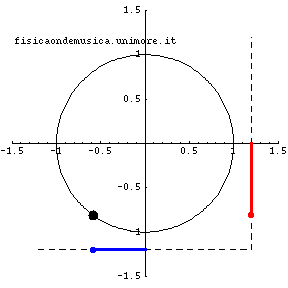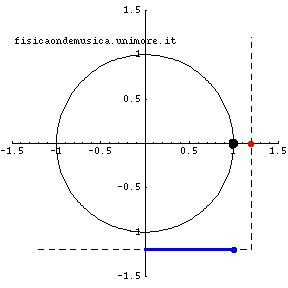
|
|
Ad ulteriore illustrazione di questi concetti si veda anche la sezione interferenza di onde armoniche.
Nell'animazione sopra riportata i punti rossi e blu si muovono di moto esattamente armonico. Essi sono le proiezioni del punto nero che si muove di moto circolare uniforme.
Perché studiare il moto armonico
Avrai sicuramente pensato che al di là della curiosità matematica di essere la proiezione di un moto estramemente semplice come quello di un punto che "gira" con velocità costante su di una circonferenza, il moto armonico non si presta a descrivere la miriade di oscillazioni che si presentano in natura (pensa al moto del pennino di un sismografo, all'oscillazione delle strutture di un edificio durante un terremoto, alla vibrazione della corda di uno strumento musicale, ecc.). Il moto armonico appare realmente troppo semplice: perché perdere tempo a studiarlo anziché risolvere problemi più realistici?
- In primo luogo proprio perché è semplice, e quindi ne possiamo comprendere tutti gli aspetti, e dedurne proprietà e teoremi in modo esatto.
- Ma soprattutto perché il moto armonico ha una universalità molto profonda. Grazie alle sue proprietà matematiche, esso compare (diremmo quasi nostro malgrado) in tutti i settori della fisica, e, sorprendentemente, anche quando il moto o l'oscillazione che si sta studiando non è affatto armonica. In particolare:
- Il teorema di Fourier stabilisce che (quasi) qualunque oscillazione (cioè qualunque funzione periodica) può essere espressa come somma di funzioni armoniche
- (Quasi) ogni sistema oscillante è ben approssimato da un oscillatore armonico se l'ampiezza delle oscillazioni è piccola.
Lasciamo l'analisi del teorema di Fourier ad un'altra sezione, mentre illustriamo l'ultimo punto di seguito mediante un esempio.
Approssimazioni armoniche
Supponiamo di avere un sistema in equilibrio stabile. Esso potrebbe essere
- una pallina in fondo ad una buca;
- un pendolo appeso ad un filo nella sua posizione verticale;
- la corda di uno strumento musicale;
- una qualsiasi struttura che "sta in piedi" (un ponte, una casa, ecc.);
- tutte le acque del pianeta terra;
- una molecola;
- un cristallo.
- Se tale sistema viene allontanato in qualunque modo dalla sua posizione di equilibrio, agiranno su di esso delle forze di richiamo che tenteranno di riportarlo all'equilibrio.
- In generale tali forze saranno funzioni complicate degli spostamenti degli elementi del sistema.
- Tali forze si devono annullare nella configurazione di equilibrio (questa è proprio la definizione di "equilibrio");
Ecco dove interviene l'approssimazione armonica:
- se immaginiamo che lo spostamento dalla condizione di equilibrio sia piccolo, potremmo assumere (quello che i matematici chiamano sviluppo al prim'ordine) che tali forze di richiamo siano proporzionali allo spostamento.
- In queste ipotesi si dimostra che il moto complessivo del sistema può essere ricondotto ad un insieme di tanti moti armonici semplici quanti sono gli elementi oscillanti che compongono il sistema
Nel seguito analizziamo il moto armonico in modo più rigoroso, e, in particolare, vedremo il caso del sistema massa-molla, che può essere usato come prototipo per tutte le oscillazioni armoniche.
Cinematica del moto armonico
Il moto circolare uniforme
Vi è una situazione geometrica nella quale l'oscillazione armonica fa la sua comparsa in modo estremamente naturale. Per descriverla abbiamo bisogno di introdurre brevemente la cinematica del moto circolare uniforme. Consideriamo un punto P che percorre una circonferenza con velocità costante. E' utile, per descrivere geometricamente tale moto, introdurre alcune grandezze di immediata interpretazione fisica:
- il periodo T definito come il tempo necessario a compiere un giro completo. Esso si misura, ovviamente, in secondi;
- la frequenza o definito come il numero di giri compiuti nell'unità di tempo. Essa si misura in Hertz , sinonimo di giri al secondo. E' facile rendersi conto che periodo e frequenza sono inversamente proporzionali cioè che
-
(1)
- la velocità tangenziale (o lineare) v definita, come per ogni moto "uniforme", come il rapporto tra lo spazio percorso ed il tempo impiegato per percorrerlo. Se come spazio percorso prendiamo proprio un giro completo si ottiene
-
(2)
- la velocità angolare o (frequenza angolare) definita come il rapporto tra l'angolo al centro percorso (misurato in radianti) e il tempo impiegato per percorrerlo. Se come angolo percorso scegliamo proprio l'angolo giro ( radianti) otteniamo
-
(3)
Si osservi che, grazie alla scelta di misurare gli angoli in radianti (ecco il motivo fisico che rende "naturale" tale misura!) si ottiene, confrontando la (2) con la (3):
-
(4)
- Si dimostra infine che il moto circolare uniforme è un moto accelerato; tale affermazione appare, a prima vista, contro intuitiva: nel linguaggio comune si associa l'accelerazione ad una variazione di velocità (che nel moto circolare uniforme sembra non essere presente). Tuttavia occorre osservare che se anche la velocità non cambia numericamente essa cambia continuamente direzione (i fisici dicono che la velocità istantanea è un vettore tangente alla traiettoria). E' possibile dimostrare che l'accelerazione nei moti circolari uniformi:
- è diretta, istante per istante, verso il centro della circonferenza (per tale motivo essa viene chiamata accelerazione centripeta)
- essa è costante (numericamente) e il suo valore si ottiene dalla formula
-
(5)
Il moto armonico come "proiezione" del moto circolare uniforme
Siamo ora pronti a presentare un esempio notevole di moto armonico: proiettiamo il punto P si di una retta e chiamiamo Q la sua proiezione. E' immediatamente evidente che il punto Q oscillerà tra la posizione e la posizione . Dimostreremo che Q si muove di moto armonico semplice cioè con una legge oraria rappresentata da una funzione sinusoidale. Per dimostrare tale fatto assumeremo:
- che all'istante t=0 il punto P si trovi in una posizione che corrisponde, per il punto Q alla ascissa x=0
- che il punto P si muova con velocità angolare costante e che abbia quindi percorso, come immediata conseguenza della (2) dopo il tempo t (a partire dall'istante iniziale t=0) un angolo α=ωt
- che le grandezze cinematiche (posizione, velocità ed accelerazione) che descrivono il moto di Q siano le proiezioni sulla retta delle corrispondenti grandezze relative a P (si pensi ad esempio ad un punto luminoso che, nella notte, ci viene incontro in direzione perpendicolare alla linea "visuale" degli occhi; tale punto ci apparirà fermo. Se il punto luminoso si avvicina obliquamente noi percepiremo solo la velocità parallela alla linea visuale e non l'intera velocità del punto luminoso).
| proiezione del raggio vettore | proiezione della velocità | proiezione dell'accelerazione |
|---|---|---|
Con queste assunzioni è facile dimostrare che
- la posizione di Q all’istante t è data da
-
(6)
avendo applicato la definizione di seno al triangolo rettangolo OPH;
- la velocità di Q all'istante t è data da
-
(7)
avendo applicato la definizione di coseno al triangolo rettangolo PST e la relazione (4) tra velocità v e velocità angolare ;
- l'accelerazione di Q all'istante t è data da
-
(8)
avendo utilizzato di nuovo la definizione di seno e la formula (5) per l'accelerazione centripeta.
Il segno meno è dovuto al fatto che, come si vede facilmente dalla figura, l’accelerazione è sempre di segno contrario rispetto alla x(t) del punto. Confrontando la (6) e la (8) si ottiene il notevole risultato
-
(9)
che si può riassumere dicendo che in un moto armonico l’accelerazione a(t) è sempre proporzionale alla posizione x(t) secondo una costante di proporzionalità negativa. Questo offre un'ulteriore caratterizzazione del moto armonico (oltre a quella di avere una legge oraria di tipo sinusoidale) che sarà molto utile per individuare "l'armonicità" del moto di altri sistemi oscillanti.
Un'ultima osservazione: è possibile riottenere i risultati delle equazioni dalla (6) alla (9) svincolandosi dall'ipotesi che il punto P si trovi, all'istante t=0, in una posizione che corrisponde, per il punto Q, all'ascissa x=0. Ciò può essere fatto semplicemente introducendo un angolo di fase (o semplicemente una fase) che indichi la posizione iniziale del punto P. Tale angolo dovrà essere sommato a per fornire la posizione del punto P dopo un tempo t. Tutte le formule potranno essere riscritte tenendo conto di questo fatto. Ad esempio la (6) diventerà
-
(6')
Dinamica del moto armonico
L'esempio precedente non può certo aver convinto il lettore della centralità del moto armonico nelle oscillazioni che avvengono realmente in natura: esso appare poco più che una curiosità geometrica. Tuttavia l'ulteriore caratterizzazione del moto armonico che esso ci ha permesso di derivare ci consentirà di dimostrare, nel paragrafo successivo, che un semplice sistema massa-molla si muoverà di moto armonico.
Sistemi massa-molla
-
(10)
La costante k fornisce una misura della "durezza" della molla: più precisamente essa è la forza di richiamo per unità di lunghezza.
Applicando al sistema massa-molla il secondo principio della dinamica otteniamo
-
(11)
da cui
-
(12)
L'accelerazione è dunque proporzionale allo spostamento secondo una costante di proporzionalità negativa. Ma questa è proprio la caratterizzazione del moto armonico che si era introdotta con l'equazione (16) a patto di considerare
-
(13)
La massa M si muoverà allora secondo la legge oraria
-
(6")
con velocità variabile nel tempo data da
-
(7")
dove, per svincolarci completamente dall'origine del moto armonico come proiezione di un moto circolare, abbiamo chiamato l'ampiezza A. È ovvio che anche ω perde il suo significato cinematico di velocità angolare; essa diventa
- in senso puramente algebrico, la grandezza tramite la quale calcolare il periodo dell'oscillazione, mediante la relazione
-
(3)
- in senso più fisico, la grandezza il cui quadrato fornisce la forza di richiamo per unità di lunghezza e unità di massa, essendo
Si osservi che, nel caso del sistema massa-molla, il periodo dell'oscillazione diventa
-
(14)
Ricordando la (1) è poi facile ottenere la frequenza naturale o frequenza di risonanza f0 dell'oscillatore
-
(15)
Si osservi che il periodo e la frequenza sono indipendenti dall'ampiezza delle oscillazioni.
La 13 fornisce, al variare dei valori delle costanti A e φ infinite leggi orarie: il sistema oscillante selezionerà una sola di queste in modo da soddisfare determinate condizioni iniziali in cui si trova all'istante uguale t=0. Fissare le condizioni iniziali di un sistema dinamico significa precisare:
- la posizione iniziale (nel caso in esame il valore di
- la velocità iniziale (nel caso in esame il valore di
Ad esempio
- nel caso ovvio che il sistema si trovi, all'istante , fermo in equilibrio nel punto di coordinata , imporre alle equazioni 6 e 7 le condizioni iniziali significa risolvere il sistema
che fornisce immediatamente la soluzione
che corrisponde all'assenza di moto (il sistema è in equilibrio stabile).
- nel caso, più interessante, in cui il sistema si trovi, all'istante , fermo nel punto di coordinata , imporre alle equazioni 6 e 7 le condizioni iniziali significa risolvere il sistema:
che fornisce immediatamente la soluzione
- .
Tale situazione corrisponde ad un'oscillazione del sistema che avviene tra i punti di coordinate x=± A0 nei quali avviene un'inversione del moto: la velocità si annulla e cambia di segno.
L'energia meccanica nei moti armonici
Il sistema massa-molla possiede due tipi di energia:
- l'energia cinetica che è l'energia che la massa possiede a causa della propria velocità e vale
- l'energia potenziale che è l'energia dovuta alla deformazione elastica della molla e vale
- .
Durante il moto oscillatorio
- queste due energie si trasformano alternativamente l'una nell'altra e , come dimostreremo, la loro somma rimane costante;
- l'energia potenziale è massima quando la molla si trova nella posizione di massima deformazione cioè per ;
- l'energia cinetica è massima quando la massa possiede la massima velocità cioè quando transita dal punto .
Volendo calcolare l'energia totale del sistema meccanico oscillante (cioè la sua energia meccanica) ad un dato istante t, dobbiamo sommare la sua energia cinetica e potenziale:
-
(23)
otteniamo
-
(24)
Sostituendo alla (24) le equazioni (13) e (14) già ricavate per il moto armonico
otteniamo
-
(25)
da cui, essendo per la (20)
- ,
si ottiene, raccogliendo ,
-
(26)
che, per la nota relazione fodamentale della trigonometria, diventa infine
-
(26)
Si osservi che, mentre separatamente le energie cinetica e potenziale cambiano nel tempo, l'energia meccanica non dipende più dal tempo. Essa è perciò una costante del moto.
Approfondimenti e collegamenti
In tutto il testo si trovano riferimenti al moto armonico, e in particolare nelle sezioni seguenti:
- oscillatori accoppiati
- onde armoniche
- teorema di Fourier
- risonanza
- modi normali
- onde stazionarie
- strumenti musicali
- percezione del suono













_armonico.png)
_armonico.png)
_armonico.png)