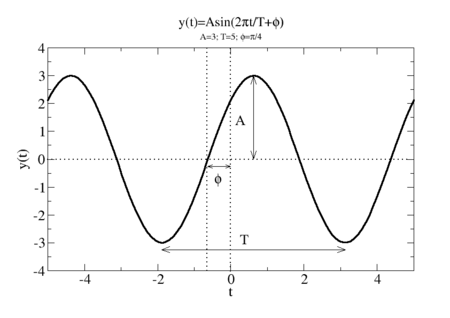
Immaginiamo che il moto oscillatorio di una sorgente sia descritto dalla funzione

${\displaystyle y_{S}(t)=A\sin(\omega t+\phi )\!}$

(1)

(Per una rapida introduzione alle funzioni trigonometriche vedi la pagina funzione seno). In questo caso diciamo che la sorgente oscilla di moto armonico, e quindi essa produce un'onda armonica.

simbolo significato ${\displaystyle A\!}$ ampiezza della sinusoide ${\displaystyle \omega \!}$ frequenza angolare. Essa è legata al periodo T dall'espressione ${\displaystyle \omega ={\frac {2\pi }{T}}}$ ${\displaystyle \phi \!}$ fase dell'onda. Essa specifica la posizione iniziale della sorgente all'istante t=0. Si ha infatti ${\displaystyle y_{S}(0)=A\sin(\phi )\!}$

Dalla sorgente all'onda

• Cerchiamo di dedurre dall'espressione (1) che descrive solo la sorgente un'espressione che descriva l'onda emessa, e cioè l'oscillazione che avviene non solo nel punto dove si trova la sorgente, ma anche in punti spazialmente distanti.
• Supponiamo perciò che l'oscillazione sinusoidale si propaghi verso destra con velocità costante v. La funzione ${\displaystyle y(x,t)}$ sarà allora data data da

${\displaystyle y(x,t)={\begin{cases}0&0\leq t<t_{\rm {rit}}\\y_{S}(t-t_{\rm {rit}})&t\geq t_{\rm {rit}}\end{cases}}}$

dove si è indicato con ${\displaystyle t_{\rm {rit}}={\frac {x}{v}}}$ il tempo di ritardo.

• Manipoliamo algebricamente l'espressione che si ottiene per ${\displaystyle t>t_{\rm {rit}}}$, al fine di ottenere un'espressione equivalente

${\displaystyle y(x,t)=y_{S}(t-t_{\rm {rit}})=A\sin \left[\omega \left(t-{\frac {x}{v}}\right)+\phi \right]}$

da cui ricordando che ${\displaystyle \omega ={\frac {2\pi }{T}}}$

${\displaystyle y(x,t)=A\sin \left[{\frac {2\pi }{T}}\left(t-{\frac {x}{v}}\right)+\phi \right]}$;

tenendo poi presente che ${\displaystyle vT=\lambda \!}$ si ottiene l'espressione particolarmente "simmetrica"

${\displaystyle y(x,t)=A\sin \left[{2\pi }\left({\frac {t}{T}}-{\frac {x}{\lambda }}\right)+\phi \right]}$;

nella quale emerge in tutta evidenza il fatto che l'onda emessa possiede una periodicità "temporale" (rappresentata dal tempo periodo T), e una periodicità "spaziale" (rappresentata dalla lunghezza d'onda ${\displaystyle {\lambda }}$); se infatti la variabile tempo t viene incrementata di un periodo T, oppure se la variabile x viene incrementata di una lunghezza d'onda ${\displaystyle {\lambda }}$, l'argomento della funzione seno aumenta proprio di ${\displaystyle 2{\pi }}$ e quindi il valore della funzione non cambia.

• Introducendo il numero d'onda ${\displaystyle k={\frac {2\pi }{\lambda }}}$ l'espressione di ${\displaystyle y(x,t)}$ diventa:

${\displaystyle y(x,t)=A\sin \left[(\omega {t}-kx)+\phi \right]}$;

Approfondimenti e collegamenti

• Se sei interessato a saperne di più sulla funzione seno visita la sezione sul moto armonico. Rimarrai sorpreso dal verificare che molte delle oscillazioni presenti in natura sono correttamente descritte da tale funzione periodica. Essa, come potrei leggere nelle pagine relative al Teorema di Fourier, è addirittura una sorta di oscillazione periodica fondamentale con la quale costruire tutti i tipi di oscillazione.
• Un utile specchietto riassuntivo delle formule usate in questa pagina si trova anche alla pagina grandezze fondamentali delle onde

---