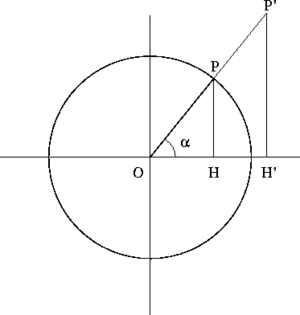
Immaginiamo di avere una circonferenza di raggio unitario e di tracciare un raggio formante un certo angolo ${\displaystyle \alpha }$ con la direzione positiva dell'asse delle X (l'angolo viene misurato convenzionalmente in senso antiorario). Il punto P in cui tale raggio incontra la circonferenza ha, per definizione, coordinate cartesiane

${\displaystyle x=\cos \alpha \,}$ (si legge coseno di ${\displaystyle \alpha }$)

${\displaystyle y=\sin \alpha \,}$ (si legge seno di ${\displaystyle \alpha }$)

Dalla definizione data derivano alcune ovvie conseguenze:

• il seno e il coseno di un angolo assumono valori compresi tra -1 e +1;
• applicando il teorema di Pitagora al triangolo OPH si ottiene

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1\quad \forall \alpha \in \mathbb {R} }$

(1)

• le funzioni seno e coseno si ripetono per ogni incremento dell'angolo di 360° (o ${\displaystyle 2\pi )}$ radianti. In modo più formale i matematici scrivono:

${\displaystyle \cos \alpha =\cos(\alpha +2k\pi )\quad \forall k\in \mathbb {Z} }$

(2)

${\displaystyle \sin \alpha =\sin(\alpha +2k\pi )\quad \forall k\in \mathbb {Z} }$

(2')

• se consideriamo un triangolo rettangolo O'P'H' simile al triangolo OPH possiamo fornire (almeno per gli angoli acuti) un'altra interpretazione geometrica del seno e del coseno di un angolo. Dalle proporzioni:

${\displaystyle {\overline {OP}}:{\overline {PH}}={\overline {O'P'}}:{\overline {P'H'}}}$,

e

${\displaystyle {\overline {OP}}:{\overline {OH}}={\overline {O'P'}}:{\overline {O'H'}}}$

possiamo immediatamente ricavare che

${\displaystyle \sin \alpha ={\frac {\text{cateto opposto}}{\text{ipotenusa}}}}$, ${\displaystyle \cos \alpha ={\frac {\text{cateto adiacente}}{\textrm {ipotenusa}}}}$

(3)

Se tracciamo il grafico delle funzioni ${\displaystyle f(x)=\sin(x)}$ e ${\displaystyle f(x)=\cos(x)}$ ci rendiamo subito conto che esse potrebbero essere adatte a rappresentare l'ampiezza dell'oscillazione di un corpo oscillante in funzione del tempo non appena si sostituisca all'ascissa x, il tempo t o qualche grandezza ad esso proporzionale.

Si pensi ad esempio al "pennino" di un sismografo che, oscillando avanti ed indietro, rilevi le oscillazioni locali di un terremoto, oppure al "pennino" di elettrocardiografo che, oscillando, rileva i battiti del nostro cuore: se facciamo scrivere questo pennino su di un rotolo di carta che si svolge con velocità costante, simulando lo scorrere del tempo, otterremo un grafico dell'ampiezza delle oscillazioni in funzione del tempo. Ovviamente non vi è alcun motivo che le oscillazioni così ottenute siano di tipo sinusoidale (saremmo anzi meravigliati del contrario!). Ma il "gran libro della natura" spesso ci sorprende: vedremo che le oscillazioni sinusoidali (che chiameremo d'ora in poi armoniche) sono presenti in molte situazioni concrete ed anzi, costituiscono, come spiegato nella sezione Teorema di Fourier, una sorta di oscillazione fondamentale con la quale descrivere ogni tipo di oscillazione periodica.

---