In questa sezione ricaviamo l'equazione delle onde in un caso ideale, ma molto utile per le applicazioni pratiche dell'acustica (v. marimba, xilofono, campane tubolari) e dell'ingegneria (sollecitazioni sulle travi, onde sismiche).

Dopo aver definito con cura il sistema procederemo in tre semplici passaggi:

1. bilancio delle forze
2. individuazione della grandezza da utilizzare come funzione d'onda
3. scrittura dell'equazione del moto

Che cos'è una barra

• A differenza della corda, la barra che qui consideriamo è un vero sistema elastico tridimensionale. Al suo interno si esercitano forze che non sono solo longitudinali, ma possono essere dirette in qualunque direzione.
• Il fatto che si tratti di una "barra", cioè di un oggetto più lungo che largo, in questo caso, serve solo per ridurre il numero di dimensioni nelle equazioni, ma non è una proprietà critica (almeno finché la barra non diventa una guida d'onda)
• La barra che consideriamo è comunque ideale perché assumiamo che la sua elasticità sia perfettamente lineare, cioè che la deformazione sia direttamente proporzionale alla forza che l'ha provocata (legge di Hooke).

La Forza elastica è direttamente proporzionale alla Deformazione

• La costante di proporzionalità non è in generale una semplice costante, ma un oggetto detto tensore, che tiene conto del fatto che una forza esercitata in una direzione, potrebbe in realtà dare luogo ad una deformazione in tutt'altra direzione.

• Comunque nei casi più semplici questo oggetto si può ridurre a poche costanti. Ciascuna di esse descrive un diverso tipo di deformazione. Ecco perché nel seguito esaminiamo ora una per una le onde che è possibile produrre in seguito a diverse deformazioni della barra.

Onde longitudinali

Che cosa sappiamo

• Le onde longitudinali si generano per compressione (o trazione).
• La deformazione corrispondente è una compressione (o una dilatazione), che si propaga nella stessa direzione in cui si è esercitata la forza che l'ha prodotta.
• La costante di proporzionalità tra la deformazione e la pressione che la produce è detta modulo di Young Y.
• L'equazione del moto di Newton per le traslazioni

${\displaystyle F=ma\!}$

Che cosa vogliamo ricavare

• Assumiamo che una compressione (o una dilatazione) avvenga lungo l'asse della sbarra nella direzione x.
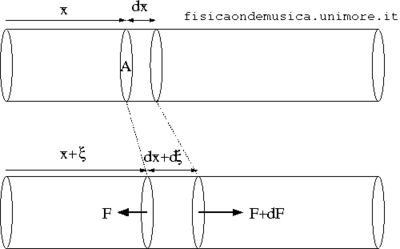
• Vogliamo ricavare l'equazione del moto per la deformazione ${\displaystyle \xi (x,t)}$ di un elemento infinitesimo della barra di sezione A e di altezza dx posto nella posizione x.

Dimostrazione

• L'elemento infinitesimo della della sbarra viene deformato in un elemento di lunghezza ${\displaystyle dx+d\xi \!}$.
• Ricordiamo che ciò che si propaga nella barra è la compressione, e perciò la grandezza rilevante è ${\displaystyle \xi }$, e non x.
• La deformazione è data da ${\displaystyle {\frac {\partial \xi }{\partial x}}}$, e, per la legge di Young abbiamo

${\displaystyle F(x(t))=AY{\frac {\partial \xi }{\partial x}}}$.

Questa equazione ci dà il valore di F, ma noi siamo interessati alla forza netta che si esercita sull'elementino di volume (v. figura), che è

${\displaystyle F(x+dx)-F(x)=dF={\frac {\partial F}{\partial x}}dx}$.

• Dobbiamo perciò derivare la formula di Young rispetto ad x, e otteniamo

${\displaystyle {\frac {\partial F}{\partial x}}dx=YA{\frac {\partial ^{2}\xi }{\partial x^{2}}}dx}$

• Per la legge di Newton questa foza va eguagliata al prodotto ma per l'elementino, che è

${\displaystyle ma=\rho Adx{\frac {\partial ^{2}\xi }{\partial t^{2}}}}$

• Eguagliando i due termini troviamo

${\displaystyle YAdx{\frac {\partial ^{2}}{\partial x^{2}}}\xi (x,t)=\rho Adx{\frac {\partial ^{2}}{\partial t^{2}}}\xi (x,t)}$,

che è un'equazione identica a quella per le onde trasversali nella corda, e cioè

${\displaystyle {\frac {\partial ^{2}\xi }{\partial x^{2}}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}\xi }{\partial t^{2}}}}$,

tranne per il fatto che la velocità di propagazione è data da

${\displaystyle c={\sqrt {\frac {Y}{\rho }}}}$.

Onde flessurali

Che cosa sappiamo

• Le onde flessurali si generano in seguito ad una flessione della barra.
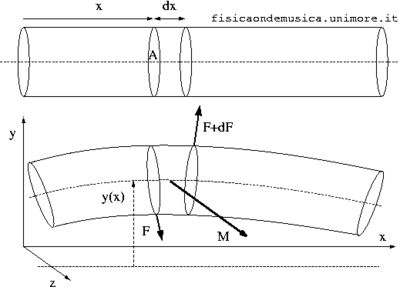
• La flessione si produce quando una coppia di forze opposte, ma non applicate nello stesso punto, agisce sulla barra in un piano contenente l'asse longitudinale (v. figura).
• Se la barra fosse un corpo perfettamente rigido essa tenderebbe a ruotare, anziché deformarsi, quindi non basta ricorrere all'equazione del moto F=ma, ma dobbiamo anche utilizzare l'equivalente per la rotazione, e cioè

${\displaystyle M=I{\frac {d^{2}\theta }{dt^{2}}}}$,

dove M è il momento della forza applicata (momento flettente), I il momento d'inerzia della sbarra rispetto ad un asse perpendicolare all'asse longitudinale, e ${\displaystyle \theta }$ l'angolo di rotazione.

• Anche in questo caso l'elasticità perfetta si esprime con una legge di proporzionalità tra il momento flettente applicato e la curvatura ottenuta. La costante di proporzionalità Y è la costante elastica (modulo di Young) della barra.

Che cosa vogliamo ricavare

• Assumiamo che la flessione avvenga lungo l'asse y della sbarra, perpendicolarmente all'asse longitudinale x. In questo caso il momento è diretto come l'asse z (vedi figura).
• Vogliamo ricavare l'equazione del moto per la posizione verticale y(x,t) di un elemento infinitesimo della barra di lunghezza iniziale dx posto nella posizione orizzontale x.

Dimostrazione

• Assumiamo che una flessione avvenga lungo la direzione y perpendicolare all'asse della sbarra. Ciò significa che una sezione dx della sbarra viene deformata in una sezione lunga ${\displaystyle dx+d\xi }$.
• La deformazione in questo caso è la curvatura della sbarra, che è proporzionale alla derivata seconda rispetto ad x della "forma" della sbarra y(x).
• La legge di Hooke, in questo caso impone che lo sforzo sia proporzionale alla deformazione, cioè

${\displaystyle M(x)=-YJ{\frac {d^{2}y}{dx^{2}}}}$,

dove la costante di proporzionalià è per comodità scomposta in un fattore dipendente solo dal materiale (il modulo di Young ${\displaystyle Y}$, avente le dimensioni di una pressione) e in uno dipendente solo dalla sua sezione detto momento d'inerzia di superficie ${\displaystyle J}$ (avente le dimensioni di una superficie al quadrato, cioè di una lunghezza alla quarta).

• Derivando questa relazione una volta rispetto a x otteniamo la forza ${\displaystyle F_{t}}$ (detta sforzo di taglio)

${\displaystyle F_{t}(x)=YJ{\frac {d^{3}y}{dx^{3}}}}$.

Il segno - è dovuto al fatto che la curvatura è negativa quando la concavità è verso l'alto, e cioè quando il momento flettente è positivo.

• Però a noi, al solito, interessa la quantità

${\displaystyle F_{t}(x+dx)-F_{t}(x)=dF_{t}={\frac {\partial F_{t}}{\partial x}}dx}$,

che è la forza netta agente sull'elementino infinitesimo (detta carico della barra). Il carico sull'elemento infinitesimo quindi vale

${\displaystyle dF_{t}=YJ{\frac {d^{4}y}{dx^{4}}}dx}$.

• Eguagliando il carico al prodotto ma, secondo l'equazione di Newton, troviamo

${\displaystyle YJdx{\frac {\partial ^{4}}{\partial x^{4}}}y(x,t)=\rho Adx{\frac {\partial ^{2}}{\partial t^{2}}}y(x,t)}$,

ovvero

${\displaystyle {\frac {\partial ^{4}y}{\partial x^{4}}}={\frac {1}{k^{2}}}{\frac {\partial ^{2}y}{\partial t^{2}}}}$,

con

${\displaystyle k={\sqrt {\frac {YJ}{\rho A}}}}$

• NOTA: quella che abbiamo ottenuto in questo caso è un'equazione del quarto ordine, e quindi completamente differente da quella per le onde longitudinali nella sbarra, e da quella per le onde trasversali nella corda. In questo caso non possiamo aspettarci lo stesso tipo di soluzioni.

Onde di torsione

Che cosa sappiamo

• Le onde di torsione si generano in seguito ad una torsione della barra.
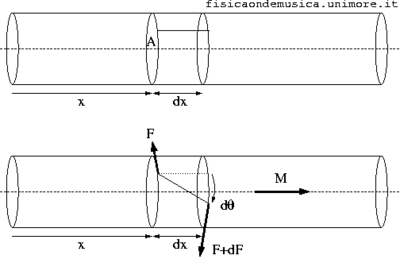
• La torsione, come la flessione si produce quando una coppia di forze opposte, ma non applicate nello stesso punto agisce sulla barra. Tuttavia, a differenza della flessione, le forze sono dirette in un piano perpendicolare all'asse della barra (v. figura).
• Anche in questo caso dobbiamo utilizzare l'equazione del moto per la rotazione

${\displaystyle M=I_{l}{\frac {d^{2}\theta }{dt^{2}}}}$,

dove M è il momento della forza applicata (momento torcente), ${\displaystyle I_{l}}$ il momento d'inerzia longitudinale della sbarra rispetto al suo asse, e ${\displaystyle \theta }$ l'angolo di rotazione.

• La legge di Hook impone che il momento torcente sia direttamente proporzionale alla rotazione. La costante di proporzionalità G è il modulo di taglio della barra.

Che cosa vogliamo ricavare

• Assumiamo che la flessione avvenga lungo l'asse y della sbarra, perpendicolarmente all'asse longitudinale x. In questo caso il momento è diretto come l'asse z (vedi figura).
• Vogliamo ricavare l'equazione del moto per la rotazione ${\displaystyle \theta (x,t)}$ di un elemento infinitesimo della barra di lunghezza dx e posto nella posizione x.

Dimostrazione

• Studiando una piccola rotazione di un angolo ${\displaystyle d\theta }$.
• La legge di Hooke si scrive

${\displaystyle M(\theta (x))=GI_{l}{\frac {\partial \theta }{\partial x}}}$

• Ci interessa, al solito la differenza tra i momenti agli estremi dell'elementino di volume

${\displaystyle M(x+dx)-M(x)=dM={\frac {\partial M}{\partial x}}dx}$,

e quindi, derivando la legge di Hooke rispetto ad x, abbiamo

${\displaystyle dM=GI_{p}{\frac {\partial ^{2}\theta }{\partial x^{2}}}dx}$

• Sostituendo nell'equazione del moto di rotazione

${\displaystyle M=I_{p}\rho {\frac {\partial ^{2}\theta }{\partial t^{2}}}dx}$

qusta diviene

${\displaystyle \rho I_{p}dx{\frac {\partial ^{2}}{\partial t^{2}}}\theta (x,t)=GI_{p}dx{\frac {\partial ^{2}}{\partial x^{2}}}\theta (x,t)}$,

e cioè

${\displaystyle {\frac {\partial ^{2}\theta }{\partial x^{2}}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}\theta }{\partial t^{2}}}}$,

• L'equazione delle onde è quindi del tutto analoga a quella delle onde longitudinali (o a quella delle onde trasversali nella corda), ma è ha come variabile l'angolo ${\displaystyle \theta }$

• La velocità di propagazione delle onde di torsione è quindi

${\displaystyle c={\sqrt {\frac {G}{\rho }}}}$

Osservazioni sulle soluzioni

Le stesse equazioni hanno le stesse soluzioni.

Basandoci su qesto principio possiamo concludere che le onde longitudinali nella sbarra, quelle torsionali, quelle trasversali nella corda, pur riferendosi a grandezze differenti, hanno esattamente le stesse proprietà.

Nella sezione equazione delle onde sonore si dimostra che anche l'equazione delle onde sonore ha la stessa forma delle precedenti.

In tutti questi casi è evidente la potenza unificatrice del concetto di onda.

---