In quasi tutti gli esempi di oscillazioni ed onde trattati in questo sito ci siamo limitati ad analizzare i fenomeni in regime lineare, anche se alcuni effetti non lineari, o anarmonici sono stati quasi sempre citati tra gli "approfondimenti" delle varie sezioni.

Il motivo principale per cui non abbiamo affrontato una vera trattazione sistematica, consiste nel fatto che gli effetti della non linearità sono molteplici e diversissimi, e la fisica dei sistemi non lineari include fenomeni completamente nuovi, rispetto al semplice moto ondulatorio. Ne sono esempi:

• l'emergenza di dinamiche caotiche, o di attrattori strani
• la presenza di nuove eccitazioni elementari del sistema che non sono onde
• l'interazione tra onde (non vale più il principio di sovrapposizione)
• la modificazione del comportamento dei modi normali del sistema: essi non sono più indipendenti tra di loro, ma sono accoppiati, e quindi non corrispondono più ad onde stazionarie.
• la modificazione delle risonanze e delle frequenze proprie del sistema
• la presenza di fenomeni di isteresi o saturazione

ecc.

Nel seguito cerchiamo di chiarire i termini e portare un solo, ma importante esempio.

Altri esempi, più complessi, ma più interessanti, si trovano nelle sezioni catena di Fermi-Pasta-Ulam e Instabilità modulazionale.

Regime lineare e non lineare

Chiariamo i termini

• Un singolo oscillatore si trova in regime lineare quando è un oscillatore armonico, e cioè quando la forza di richiamo è direttamente proporzionale alla distanza dell'oscillatore da un punto, che ne costituisce il punto di equilibrio

${\displaystyle \mathbf {F} =-k(\mathbf {x} -\mathbf {x} _{0})}$.

Questa forza quindi ammette un potenziale direttamente proporzionale al quadrato della distanza dal punto di equilibrio

${\displaystyle V={\frac {1}{2}}k(\mathbf {x} -\mathbf {x} _{0})^{2}}$.

• Un sistema di N oscillatori si trova in regime lineare quando ciascun oscillatore è soggetto a un insieme di forze armoniche. Per esempio l'i-esimo oscillatore sarà soggetto ad una forza complessiva pari a

${\displaystyle \mathbf {F} _{i}=-\sum _{j}^{N}k_{j}(\mathbf {x} _{i}-\mathbf {x} _{j}^{0})}$

ovvero ad un potenziale

${\displaystyle V_{i}={\frac {1}{2}}\sum _{j}^{N}k_{j}(\mathbf {x} _{i}-\mathbf {x} _{j}^{0})^{2}}$

• Regime non lineare si riferisce a tutte le situazioni che si discostano dal caso precedente.

Cosa accade nella realtà

• Dal punto di vista della realtà sperimentale, e senza ulteriori ipotesi, i sistemi fisici reali sono da considerarsi tutti non lineari.
  • Ad esempio, le forze elastiche reali non seguono la legge di Hooke per qualunque dislocazione dalla posizione di equilibrio. Ce ne si rende conto facilmente notando che un sistema elastico, al crescere della deformazione, prima risponde elasticamente, ma poi si snerva, rimane deformato in modo perenne, e poi si rompe, quando viene sollecitato oltre un certo limite. Tutti fenomeni evidentemente non lineari.
  • Dal punto di vista fisico-matematico la presenza di termini non lineari si traduce nel fatto che le forze non sono più semplicemente direttamente proporzionali agli spostamenti, ma dipendono anche dal loro quadrato, cubo, ecc. Un esempio tipico è costituito da un oscillatore il cui potenziale è

${\displaystyle V={\frac {1}{2}}k_{1}(\mathbf {x} -\mathbf {x} _{0})^{2}+{\frac {1}{3}}k_{2}(\mathbf {x} -\mathbf {x} _{0})^{3}}$.

• Tuttavia, la maggior parte dei sistemi fisici possono essere considerati approssimativamente lineari quando le oscillazioni sono abbastanza piccole.
  • Questa proprietà è equivalente ad assumere che le forze (o i potenziali) siano tutte sviluppabili in serie di potenze con un termine al primo ordine. In parole povere è come dire "la terra è piatta a tutti gli effetti, finché ne vediamo una porzione sufficientemente piccola".

Il pendolo

È straordinariamente facile ottenere comportamenti complessi anche in sistemi apparentemente molto semplici. Il comune pendolo ne è un esempio.

L'equazione del moto del pendolo determina la legge oraria del moto dell'angolo di oscillazione. Tuttavia la forza netta di richiamo (dovuta alla composizione della forza di gravità e della tensione della corda) dipende dall'altezza da terra, e cioè dal seno dell'angolo. Perciò l'equazione esatta del moto del pendolo (ferme restando le altre approssimazioni: corda ideale senza massa, massa oscillante puntiforme, moto in un piano) è pertanto

${\displaystyle \alpha +{\frac {g}{l}}\sin \theta =0}$,

(1)

dove α indica l'accelerazione angolare.

La forma comune, che riduce il pendolo ad un oscillatore armonico, invece, è in realtà la forma approssimata al prim'ordine nello sviluppo in serie della funzione seno

${\displaystyle \alpha +{\frac {g}{l}}\theta =0}$.

(2)

Utilizzando la (2) anziché la (1) si ottiene la nota espressione per il tempo periodo del pendolo

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}$,

(3)

Questa legge del moto è in accordo con l'osservazione di Galileo che il tempo periodo non dipende dall'ampiezza dell'oscillazione, ma solo l'equazione (1) descrive correttamente anche le oscillazioni di grande ampiezza. Per queste oscillazioni il periodo è dato da

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}\left(1+{\frac {1}{4}}\sin ^{2}{\frac {\theta _{max}}{2}}+{\frac {9}{64}}\sin ^{4}{\frac {\theta _{max}}{2}}+\cdots \right)}$.

(4)

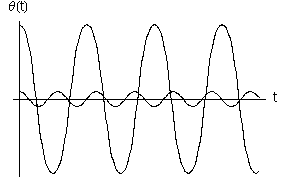
Dall'esame delle seguenti figure si nota che le oscillazioni di maggiore ampiezza hanno periodo maggiore rispetto a quelle di minore ampiezza. Inoltre la loro forma non è più sinusoidale.

Oscillazioni di 15° e 150° a confronto. Il periodo dell'oscillazione più ampia è molto maggiore di quello dell'oscillazione più piccola.	Diagramma velocità angolare-angolo (spazio delle fasi) per un'oscillazione di 15°. L'oscillazione sinusoidale genera un'ellisse (figura di Lissajous).	Diagramma velocità angolare-angolo (spazio delle fasi) per un'oscillazione di 150°. L'oscillazione non è sinusoidale, e non genera pertanto una figura di Lissajous.

L'oscillatore di Van der Pol

Un tipo di oscillatore non lineare modello che trova diverse applicazioni pratiche è l'oscillatore di Van der Pol. Esso soddisfa l'equazione

${\displaystyle {\dot {\omega }}+\theta +\mu (\theta ^{2}-1)\omega =0}$

dove ${\displaystyle \omega ={\dot {\theta }}}$ e ${\displaystyle \alpha ={\dot {\omega }}}$ indicano rispettivamente velocità ed accelerazione (angolari) dell'oscillatore.

I primi due termini descrivono un oscillatore armonico di periodo ${\displaystyle 2\pi \;}$, poiché la costante di proporzionalità tra accelerazione angolare ed angolo ha modulo uguale a 1; l'ultimo termine è responsabile del comportamento non lineare. Vediamo secondo quali modalità.

Analisi grafica

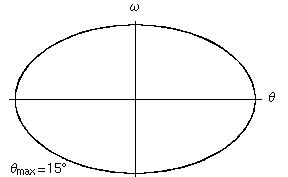
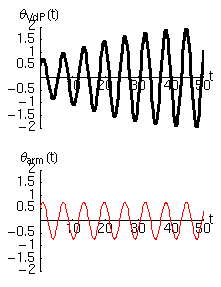
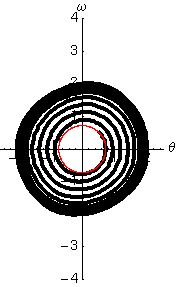
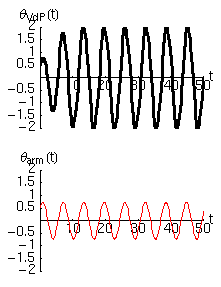
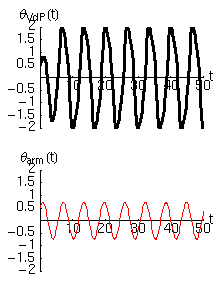
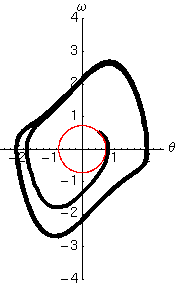
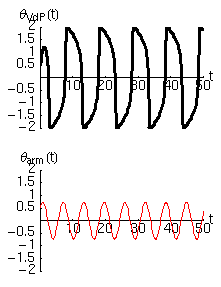
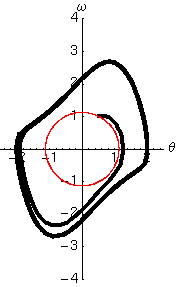
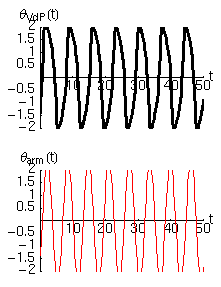
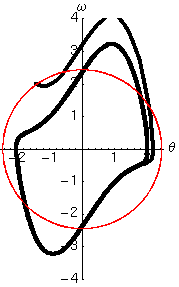
Per farci un'idea delle proprietà di questo oscillatore abbiamo risolto numericamente l'equazione di Van der Pol, e abbiamo rappresentato il moto in due modi nelle figure che seguono. Nella prima colonna si trova la solita legge del moto, in cui l'angolo di oscillazione è disegnato in funzione del tempo. Nella seconda colonna abbiamo invece rappresentato la velocità angolare in funzione dell'angolo. Questa rappresentazione (detta spazio delle fasi) ha diversi vantaggi rispetto a quella tradizionale. In particolare permette di accorgersi rapidamente se esistono dei cicli limite, o attrattori, verso i quali il moto del sistema è appunto attratto a partire da diverse condizioni iniziali.

Per avere un riferimento abbiamo tracciato la traiettoria dell'oscillatore di Van der Pol in nero, e quella dell'oscillatore armonico con le stesse condizioni iniziali in rosso.

Esaminiamo ora i tracciati. Un'ulteriore breve analisi si trova nel paragrafo seguente.

• Per la condizione iniziale scelta si nota che l'ampiezza delle oscillazioni aumenta sempre gradualmente fino a raggiungere un ciclo limite
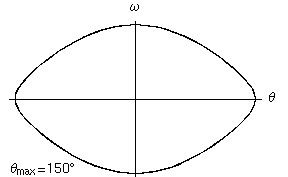
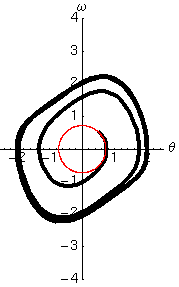
• La forma del ciclo limite dipende, oltre che dalle condizioni iniziali, dal valore del parametro ${\displaystyle \mu }$, e si discosta tanto più dal ciclo armonico (circonferenza) quanto maggiore è il valore di ${\displaystyle \mu }$.

	Legge del moto	Spazio delle fasi
${\displaystyle \mu =0.1}$
${\displaystyle \mu =0.5}$
${\displaystyle \mu =1}$
${\displaystyle \mu =4}$

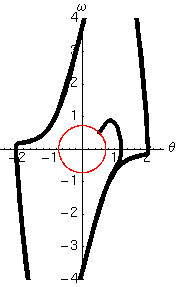
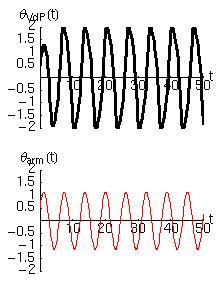
La seguente osservazione suggerisce che l'oscillatore sia robusto rispetto alle condizioni iniziali. Infatti, vediamo che un ciclo limite esiste sia che iniziamo il moto all'interno o all'esterno di esso. In altre parole, se le oscillazioni iniziali sono troppo piccole esse verranno amplificate, mentre se sono troppo grandi, verranno smorzate fino ad un valore stabile. I due cicli limite, però non saranno uguali.

${\displaystyle \mu =1.5}$	Legge del moto	Spazio delle fasi
${\displaystyle \theta (0)=30^{\circ };\omega (0)=1}$
${\displaystyle \theta (0)=-80^{\circ };\omega (0)=2}$

Approfondimenti

Vediamo come possiamo giustificare le osservazioni precedenti a partire dall'analisi dell'equazione del moto. Ricordiamo che il solo termine non lineare è quello proporzionale a ${\displaystyle \mu }$. Dall'esame dell'equazione

${\displaystyle {\dot {\omega }}+\theta +\mu (\theta ^{2}-1)\omega =0}$

vediamo che

• se ${\displaystyle \mu =0}$ l'oscillatore si riduce evidentemente ad un oscillatore armonico. Il suo moto sarà sinusuoidale puro, e il diagramma angolo-velocità seguirà una traiettoria circolare. Nelle immagini di sotto riportiamo in rosso queste linee come riferimentoò
• se ${\displaystyle \mu >0}$ il termine aggiunto ha due effetti che si compensano:
  • per oscillazioni al di sopra di un certo angolo limite (in questo caso ${\displaystyle \theta >1}$) il termine è positivo, e corrisponde ad una sottrazione di energia dall'oscillatore. In sostanza equivale ad un termine di attrito proporzionale alla velocità del moto. In sostanza, dice che le oscillazioni di grande ampiezza tendono ad essere smorzate
  • per oscillazioni al di sotto dell'angolo limite (in questo caso ${\displaystyle \theta <1}$) il termine è negativo, e corrisponde ad un'aggiunta di energia dall'oscillatore. In sostanza esso equivale ad una forza esterna proporzionale alla velocità del moto. L'aggiunta di energia significa che le oscillazioni di piccola ampiezza tendono ad essere aumentate.

Si intuisce che l'effetto netto del termine non lineare, a fissate condizioni iniziali, consiste nello stabilizzare le oscillazioni su un ciclo limite, che costituisce il punto di equilibrio tra oscillazioni troppo grandi, che tendono a smorzarsi, ed oscillazioni piccole, che invece tendono ad aumentare di ampiezza. La forma del ciclo limite si discosterà tanto più dalla circonferenza (oscillatore armonico) quanto maggiore è il valore di ${\displaystyle \mu }$.

---