Le malte e i calcestruzzi che si utilizzano nelle costruzioni civili sono materiali con tantissime pregevoli proprietà, ma sono quasi sempre caratterizzati da una bassa resistenza alla trazione. Ne sono indice le crepe che si vedono su quasi tutti gli edifici di una certa età. Per questo motivo la moderna scienza delle costruzioni ha trovato il rimedio di rinforzare le strutture mediante tondini d'acciaio (materiale invece assai resistente a questo tipo di sforzo). Ne è nato il cemento armato, con il risultato che i terremoti di debole o media entità creano pochissimi danni seri ai moderni grattacieli, mentre causano terribili devastazioni nei paesi meno sviluppati in cui le case sono costruite con pietre o mattoni legati da malte primitive.

Vogliamo qui brevemente illustrare come lo studio delle risonanze di un edificio, fissate le proprietà dei materiali con cui esso è stato costruito, possa fornire utili indicazioni per la progettazione di edifici più resistenti alle sollecitazioni dinamiche, e, in particolare, dei terremoti.

Un'analisi dinamica semplificata

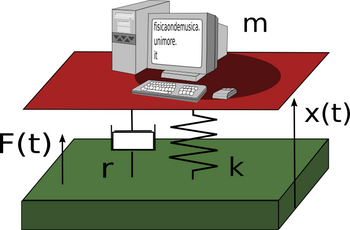
Dal punto di vista delle sollecitazioni meccaniche è utile considerare ogni edificio, come un sistema meccanico formato da parti massicce, ma virtualmente inelastiche, e parti di collegamento leggere ed elastiche. Se a questo punto "masse e molle" e "approssimazione lineare" non vi dicono niente provate a vedere nelle sezioni dedicate al principio di sovrapposizione, ai modi normali, all'impedenza.

Gli edifici non sono sempre facilmente descritti da semplici modelli lineari, ma lo studio dei modelli lineari è il primo passo per una comprensione, anche se approssimata, della loro dinamica.

Dato un modello lineare, per quanto complesso esso sia, infatti, sappiamo che, a patto di opportune manipolazioni matematiche, esso è sempre scomponibile in un insieme di oscillatori semplici e indipendenti. Ad ogni modo normale corrisponde una risonanza del sistema. Cioè una frequenza propria alla quale il sistema è particolarmente vulnerabile. Infatti una forza esterna, anche di moderata intensità, ma della frequenza corretta, è in grado di indurre nel sistema oscillazioni che possono crescere tanto da superare gli sforzi massimi tollerabili dal sistema stesso, e mandarlo in pezzi.

modello fisico	modello dinamico	simulazione dinamica

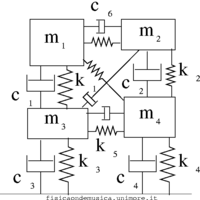
La simulazione qui sopra raffigurata mostra un semplice modello a "masse e molle" mostra la risposta di un sistema relativamente semplice ad una sollecitazione sinusoidale alla base (tipo un terremoto). La scala dei colori indica la compressione o dilatazione degli elementi. In questa pagina dello Structural Control and Earthquake Engineering Laboratory dell'università di Washington trovate un'ottima serie di filmati che mostrano modelli in scala di edifici sottoposti a diverse sollecitazioni.

Ciò che dobbiamo fare è allora studiare la risposta del sistema alle sollecitazioni, ed, eventualmente, progettare sistemi oscillanti ausiliari da introdurre nell'edificio affinché le sue risonanze alle frequenze critiche vengano opportunamente smorzate. Un esempio di questa tecnica porta alla costruzione degli smorzatori sismici, e di altri sistemi per lo smorzamento delle oscillazioni autoindotte.

Smorzatori sismici

Nella pagina sulla risonanza nei motori si mostra come si possa isolare un sistema soggetto ad una vibrazione dalla base su cui essi poggia trasformandolo in un oscillatore, e modificandone adeguatamente massa, rigidità, ed attrito.

Ma cosa fare se la sorgente delle oscillazioni è proprio il basamento?

Questo è proprio il caso interessante per gli edifici soggetti a forze sismiche: l'edificio in sé può essere considerato un complesso sistema oscillante (vedi il paragrafo precedente), e il basamento (cioè la terra su cui esso poggia), oscilla in modo irregolare. Possiamo sfruttare le risonanze dell'edificio a nostro vantaggio? Oppure: possiamo modificarle a nostro vantaggio?

La buona notizia è che conosciamo già la funzione di risposta del sistema. Infatti la risposta in ampiezza, cioè la massima ampiezza di oscillazione del sistema in funzione della massima ampiezza di oscillazione del basamento, è identica alla risposta in forza del sistema con basamento fisso, cioè la massima forza trasmessa al basamento come funzione della massima forza applicata sul sistema. Non dimostriamo questa affermazione, ma invitiamo a osservare l'andamento della funzione risposta alla pagina risonanza nei motori.

Abbiamo già tre soluzioni: cambiare la massa dell'edificio, cambiare la sua elasticità, aumentarne gli attriti. Però non è facile cambiare la massa, perché l'edificio è progettato per sopportare un certo carico statico, ed aumentarlo non è un'idea brillante. Per quanto riguarda le altre due possibilità possiamo pensare di montare tutto quanta la costruzione su un basamento elastico e incorporarvi degli smorzatori ad attrito viscoso. Per quanto incredibile possa sembrare questa soluzione è possibile, ed è stata messa in pratica, ad esempio, per l'edificio storico della City Hall di Los Angeles raffigurato qui a fianco. L'ammortizzamento sismico è ottenuto mediante 416 bande di gomma elastica, e 64 smorzatori viscosi.^[1]

Esiste però anche un'altra possibilità che non abbiamo ancora considerato. Di nuovo, per afferrarne il principio, studiamo un sistema semplificato, di nuovo un oscillatore armonico ad un grado di libertà.

Assorbimento delle vibrazioni

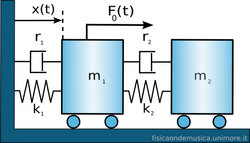
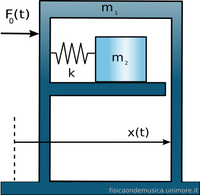
Supponiamo di avere una massa m₁ vibrante. Cosa accade se anziché modificare i parametri dell'oscillatore esistente lo colleghiamo con un altro oscillatore di massa m₂? Alla pagina oscillatori accoppiati si trova per esteso la teoria riguardante le oscillazioni libere di due oscillatori armonici collegati da una molla. Qui il caso è molto simile: vogliamo studiare le oscillazioni forzate del sistema. Le differenze sono che la forza esterna è trasmessa dal basamento, e che abbiamo solo due "molle" anziché tre.

Vale comunque un principio generale (già enunciato nella pagina introduttiva sulla risonanza): il sistema complessivo dei due oscillatori ha due gradi di libertà. Ci aspettiamo quindi che abbia due risonanze, anziché una sola.

Ma allora non abbiamo peggiorato la situazione?

Dipende: posto che qualunque sistema meccanico possiede frequenze proprie e risonanze in corrispondenza di tali frequenze, ciò a cui possiamo puntare non è l'eliminazione di tutte le risonanze, ma lo smorzamento di alcune. Quali risonanze smorzare? Semplice: quelle alle quali il sistema è meno robusto (cioè quelle di ampiezza maggiore), o quelle che lo interessano più spesso in quanto corrispondono a frequenze sempre presenti nella forzante. Ad esempio non ha molto senso cercare di eliminare oscillazioni ad alte frequenze in un edificio. Di solito le frequenze pericolose sono quelle che corrispondono ai primi modi normali.

Nel nostro modello "giocattolo" c'è una sola risonanza, quindi il nostro obiettivo diventa: possiamo smorzare l'unica risonanza esistente? Dove si trovano le due nuove frequenze di risonanza del sistema composto dai due oscillatori?

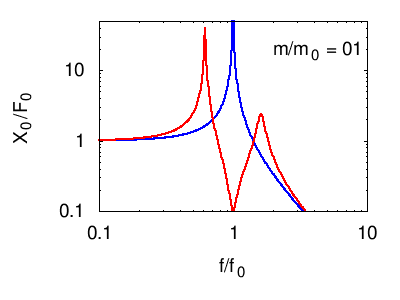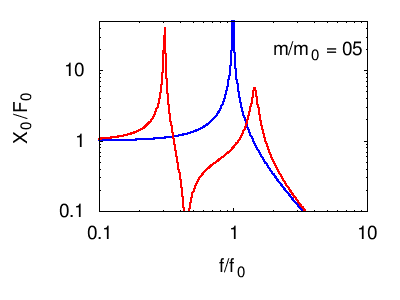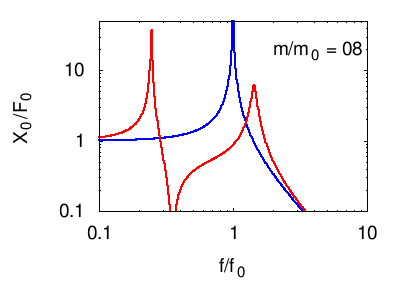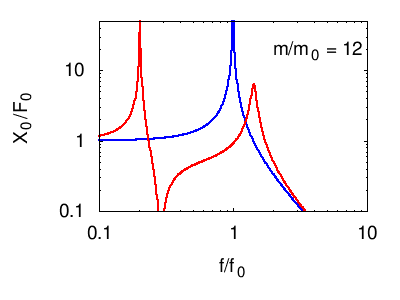
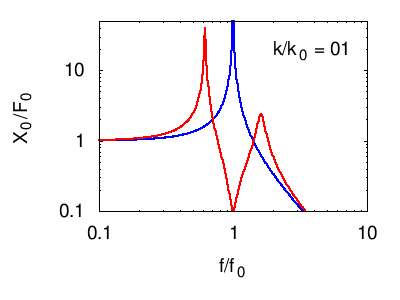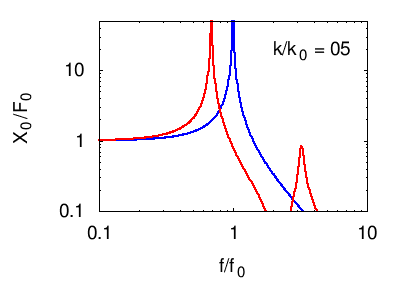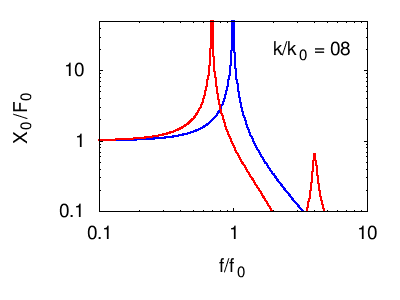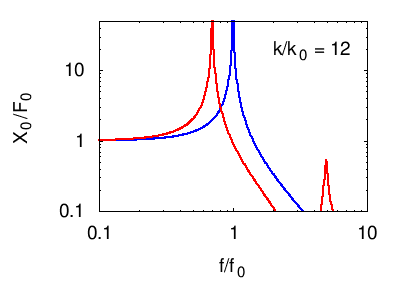
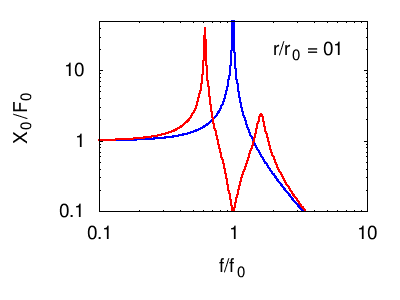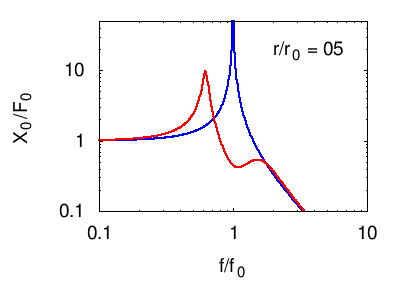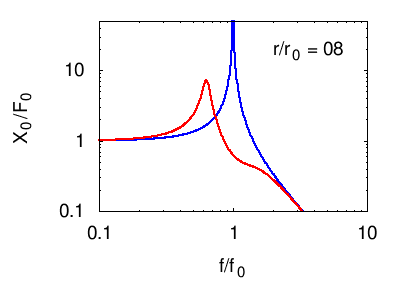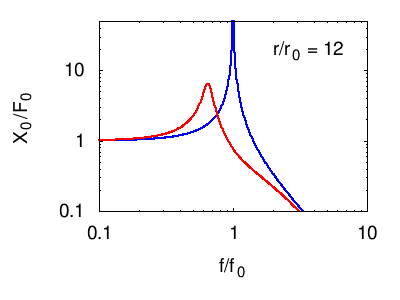
Senza entrare nel dettaglio del calcolo della risposta descriviamo ciò che accade nelle seguenti animazioni. In tutti i casi si vede che la risposta in corrispondenza della risonanza principale del sistema è fortemente smorzata, mentre compaiono due massimi "laterali" corrispondenti ai due nuovi modi normali del sistema. Naturalmente otteniamo un isolamento soddisfacente solo in un certo intervallo di frequenze attorno a f₀.

Per facilità di visualizzazione si parte dalla situazione in cui l'oscillatore principale e quello di assorbimento sono uguali m₁=m₂ e k₁=k₂. Ovviamente questo non è il caso degli edifici, in cui in genere ${\displaystyle m_{1}\gg m_{2}}$.

	Aumentare la massa dell'oscillatore di assorbimento abbassa la frequenza di risonanza inferiore, mentre ha poca influenza su quella superiore. La banda in cui il sistema non risponde alla sollecitazione esterna si allarga verso le basse frequenze.
	Aumentando la rigidità della molla tra i due oscillatori si favorisce l'oscillazione in fase delle due masse. La frequenza più bassa, al limite tende a ${\displaystyle 2\pi {\sqrt {\frac {k_{0}}{m+m_{0}}}}}$, mentre quella più elevata diviene sempre più grande. Anche in questo caso la banda delle frequenze fortemente attenuate si allarga all'aumentare di k.
	Consideriamo per semplicità solo l'attrito dell'oscillatore di assorbimento, perché quello dell'intero edificio in genere è trascurabile. Si vede che ora, fissata la posizione delle due risonanze, l'effetto dello smorzamento consiste nell'attenuare la risposta, particolarmente alle alte frequenze.

Esempi reali

Il meccanismo di assorbimento illustrato nel paragrafo precedente è stato applicato a costruzioni reali come ponti e grattacieli. Nei grattacieli e nelle torri l'aggiunta di una grande massa oscillante ai piani più alti aiuta a stabilizzare l'edificio quando esso viene posto in oscillazione. Se la fonte delle oscillazioni sono eventi sismici si preferisce un isolamento alla base come quello illustrato alla pagina risonanza nei motori, e nel paragrafo sugli smorzatori sismici, ma esistono anche altre sorgenti di forze esterne. In particolare (come anche accade per i ponti e nelle strutture sospese) sono da considerare le forze di origine idrodinamica, prodotte dal vento che incide sulla superficie esposta della costruzione.

Anche se di non forte intensità istantanea, queste forze, pur non essendo periodiche, possono dare luogo ad oscillazioni autoindotte (si veda il caso del il caso del Tacoma Narrows Bridge). L'installazione di uno smorzatore può limitare i danni alla truttura provocati dall'oscillazione. Qui sotto una fotografia della più grande massa di smorzamento al mondo: un pendolo da 662 tonnellate posto a 380 m d'altezza tra l'88° e il 92° piano della torre Taipei 101 a Taipei, Taiwan (fotografia a sinistra). A fianco lo schema di principio dello smorzatore, e un disegno tecnico degli ultimi piani della torre, che indica con precisione dove sia stata posizionata la massa oscillante.

Infine citiamo soltanto, la possibilità di ottenere un migliore controllo sulla risposta oscillatoria dei sistemi complessi mediante l'uso di smorzatori attivi. Essi sono veri e propri attuatori che agiscono in modo da contrastare attivamente le forze indesiderate che agiscono su una struttura mediante lo sviluppo di forze di contrasto, cioè in retroazione negativa, o antirisonanza volte a diminuire. Purtroppo approfondire questo interessante campo dell'ingegneria va oltre gli scopi di questa pagina.

Riferimenti e collegamenti esterni

• Un elenco di grandi strutture che montano smorzatori di vari tipi al sito del The Council on Tall Buildings and Urban Habitat.

---

---