Le figure di Lissajous

Non presentiamo qui le figure di Lissajous nella loro definizione matematica rigorosa, ma solo come un mezzo per l'analisi dei fenomeni oscillatori.

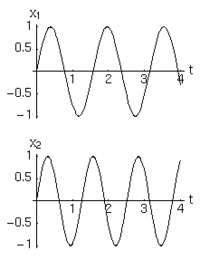
Supponiamo di dover studiare due oscillatori armonici semplici e di averne misurato sperimentalmente le leggi del moto ${\displaystyle x_{1}(t)}$ e ${\displaystyle x_{2}(t)}$ che possiamo riportare su due grafici del tipo ${\displaystyle x(t)}$.

Se ora vogliamo desumere solo da tali grafici il rapporto tra le frequenze di oscillazione e lo sfasamento relativo, ma non conosciamo a priori la soluzione analitica esatta, la sola analisi comparativa delle due leggi del moto può risultare difficoltosa (vedi figura a sinistra).

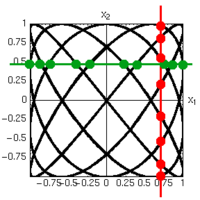
Una rappresentazione molto più efficace rispetto alle proprietà che vogliamo determinare è invece quella di un diagramma in cui il tempo non compare esplicitamente e le due grandezze ${\displaystyle x_{1}(t)}$ e ${\displaystyle x_{2}(t)}$ sono rappresentate in un grafico l'una in funzione dell'altra: ad ogni tempo fissato si ricavano cioè le ${\displaystyle x_{1}(t)}$ e ${\displaystyle x_{2}(t)}$ che diventano, rispettivamente, le ascisse e le ordinate dei punti nella nuova rappresentazione grafica. Nel caso particolarmente semplice di oscillazioni armoniche pure queste curve prendono appunto il nome di "figure di Lissajous" (figura a destra). Le figure di Lissajous si rivelano particolarmente utili poichè:

• rappresentano la traiettoria effettivamente descritta da un punto il cui moto è la sovrapposizione di due moti armonici che si sviluppano in direzioni perpendicolari;
• a partire dalle figure di Lissajous, ed è questo il nostro scopo, è immediato determinare il rapporto tra le frequenze nel caso in cui questo sia espresso da un numero razionale;
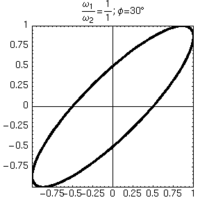
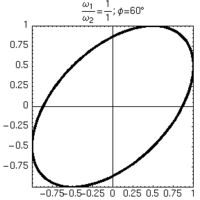
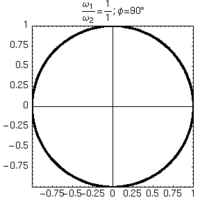
• a partire dalle figure di Lissajous è immediato anche determinare lo sfasamento dei due oscillatori nei casi particolari di angoli particolarmente semplici (es: 30°, 60° ecc...).

Illustriamo la semplice procedura grafica:

Si traccino due rette parallele agli assi, in modo che non passino per i punti in cui le linee della curva si sovrappongono. Si contino ora il numero di intersezioni di queste rette con la curva. Nel nostro caso abbiamo 10 intersezioni lungo la retta parallela all'asse ${\displaystyle x_{2}}$ (linea rossa), e 8 lungo la retta parallela all'asse ${\displaystyle x_{1}}$ (linea verde). Il rapporto tra il numero di intersezioni nelle due linee è pari al rapporto tra le frequenze rispettivamente degli oscillatori ${\displaystyle x_{1}}$ e ${\displaystyle x_{2}}$. In questo caso. ${\displaystyle {\frac {8}{10}}={\frac {f_{1}}{f_{2}}}={\frac {4}{5}}}$

Rassegna

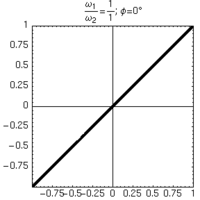
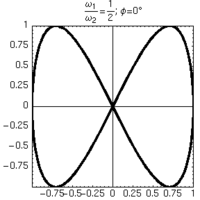
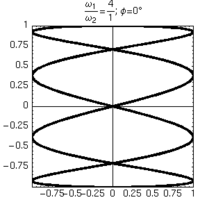
Alcune figure di Lissajous ottenute per rapporti semplici di frequenza, mantenendo lo sfasamento tra gli oscillatori pari a 0.

1:1	1:2	1:3	1:4
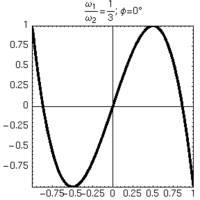
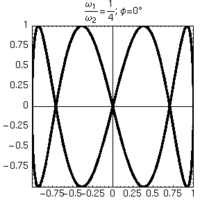
	2:1	3:1	4:1

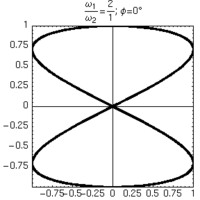
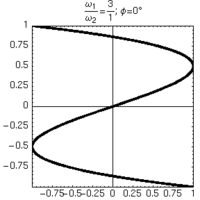
Alcune figure di Lissajous ottenute mantenendo uguali le frequenze degli oscillatori, e variandone lo sfasamento.

φ=0°	φ=30°	φ=60°	φ=90°
φ=180°	φ=150°	φ=120°

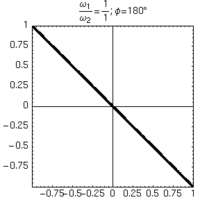
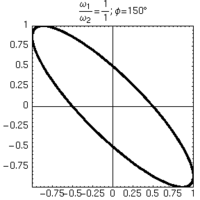
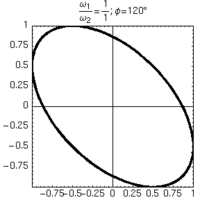
L'unico modo di distinguere sfasamenti positivi e negativi consiste nell'osservare la formazione delle figure nel tempo.

φ=+60°	φ=-60°

---
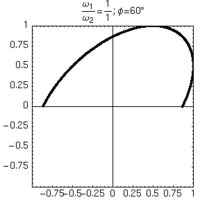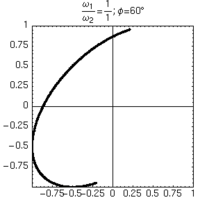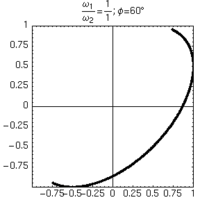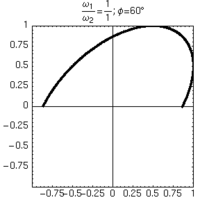
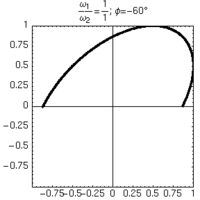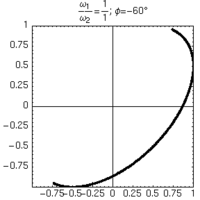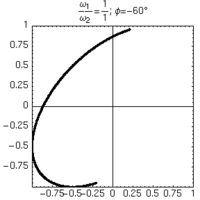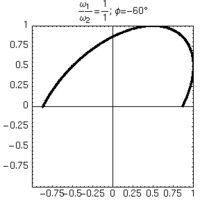