Descrizione

I risuonatori di Helmholtz sono delle particolari cavità risonanti acustiche create da Hermann von Helmholtz nel 1860 per lo studio del suono e della sua percezione. Essi possono essere semplicemente costruiti come dei recipienti di metallo (in genere sferici o cilindrici) di varie dimensioni, con una stretta apertura preceduta da un breve e stretto collo.

Funzionamento e applicazioni

Mettendo in oscillazione l'aria contenuta in un risuonatore (per esempio soffiando di taglio nell'imboccatura, o, semplicemente, esponendo il risuonatore ad una fonte di onde sonore), si generano al suo interno onde stazionarie in risonanza con la frequenza propria della cavità, che, quindi, si comporta come un amplificatore selettivo del suono in un ristretto intervallo di frequenze.

1. Un banco di risuonatori di dimensioni differenti, quindi, può essere utilizzato come uno strumento analogico di analisi del suono. In presenza di un suono complesso il banco di risuonatori lo scompone nelle sue componenti pure. La risposta di ciascun risuonatore sarà proporzionale all'intensità con cui la frequenza corrispondente contribuisce a formare il suono da analizzare. Si tratta, in pratica, di un rudimentale sistema meccanico in grado di effettuare un'analisi di Fourier in tempo reale. Grazie all'elettronica, naturalmente, queste operazioni sono svolte da un opportuno banco di filtri che operano su un segnale elettrico, ottenuto dall'originale sonoro grazie ad un microfono.
2. Helmholtz per primo utilizzò i risuonatori nello studio della sensazione sonora. Presto scoprì che un banco di risuonatori costituisce un modello piuttosto accurato per l'orecchio umano. Anche l'orecchio infatti esegue un'analisi di Fourier in tempo reale del suono che riceve, trasformando l'informazione contenuta nelle singole componenti armoniche in una codifica spaziale: armoniche di differente frequenza corrispondono ad un'eccitazione in una differente posizione all'interno della coclea. Per maggiori dettagli si veda alle pagine su anatomia e fisiologia del sistema uditivo.
3. Il principio del risonatore trova comunque applicazione negli strumenti a corda, di cui costituisce sempre il corpo cavo (vedi domande e risposte sugli strumenti musicali e violino, chitarra). La risonanza principale di Helmholtz contribuisce, a volte in modo determinante, alla risposta ed alla resa acustica di tali strumenti.
4. Un'altra applicazione consiste nel subwoofer presente nei moderni impianti Hi-Fi. La risonanza di Helmholtz di una cassa di legno di dimensioni adeguate può infatti facilitare l'irraggiamento di un altoparlante alle basse frequenze. Al di sotto di circa 80 Hz l'efficienza di irraggiamento degli altoparlanti classici diminuisce drasticamente, e, senza l'aiuto della risonanza, sarebbe impossibile emettere onde sonore con alti livelli di intensità. Esistono tuttavia anche dei "trucchi" basati sull'illusione acustica della fondamentale mancante per aumentare l'efficienza apparente di un altoparlante alle basse frequenze. Si veda la rispettiva pagina per la spiegazione.

Frequenza di un risuonatore ideale

Solo due parametri sono sufficienti per descrivere completamente un risuonatore: la sua frequenza di risonanza, e l'efficienza con cui esso risuona (ovvero l'intervallo di frequenze alle quali si ottiene una risposta). Occupiamoci solo del primo, in quanto il secondo dipende dagli attriti interni dello strumento.

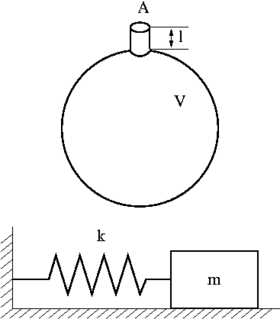
Affinché il risuonatore sia ideale supponiamo che, durante l'oscillazione della massa d'aria, l'aria stessa non esca dal recipiente, e che si muova senza attrito. In queste ipotesi l'aria contenuta nel recipiente si comporta come una molla ideale, e l'aria contenuta nel "collo" si comporta come una massa ideale. È quindi semplice concepirne un modello meccanico "a costanti concentrate", cioè considerando l'aria nel corpo della cavità come un'entità priva di inerzia, ma dotata di elasticità, mentre l'aria nel collo come un'entità dotata di inerzia, ma avente elasticità trascurabile.

Queste approssimazioni sono giustificate dal fatto che nel corpo rigido e chiuso del recipiente, l'aria è sostanzialmente immobile, mentre mantiene la sua comprimibilità elastica, mentre nel collo aperto l'aria è libera di muoversi con una velocità finita come un unico blocco, quindi, sostanzialmente senza modificare il proprio volume.

Grazie a questo modello meccanico possiamo disinteressarci del moto dettagliato del fluido, e considerarne l'oscillazione come quella di un sistema ad un solo grado di libertà.

Equivalente meccanico del risuonatore ideale

I parametri che descrivono il risuonatore ideale sono riassunti nella seguente tabella.

simbolo	significato	unità di misura nel sistema SI
l	lunghezza del collo	m
A	sezione del collo	m2
V	volume del corpo della bottiglia	m3
ρ0	densità dell'aria a riposo	kg/m2
v	velocità del suono nell'aria	m/s

Il risuonatore di Helmholtz è una bottiglia con un collo molto piccolo rispetto al corpo, cioè deve valere la relazione

${\displaystyle V\gg Al}$.

• Il sistema è del tutto equivalente al sistema meccanico massa-molla (si veda analogie in fisica).
• L'aria all'interno del corpo cavo corrisponde alla molla, in virtù del fatto che è comprimibile. Maggiore è il volume V del recipiente minore è la sua costante elastica equivalente (cioè meno rigido è il sistema). La costante elastica equivalente (si veda cedevolezza acustica) è

${\displaystyle k={\frac {\rho _{0}c^{2}A^{2}}{V}}}$,

dove c è la velocità del suono in aria, e ρ₀ la densità dell'aria.

• L'aria presente nel "collo" corrisponde alla massa oscillante. La sua caratteristica principale è l'inerzia che essa possiede una volta messa in oscillazione. Essendo in piccola quantità la sua compressibilità è trascurabile. Una imboccatura stretta tende a immobilizzare l'aria (grande inerzia), mentre con un'imboccatura larga è molto facile spostare l'aria dentro e fuori dalla bottiglia. La massa d'aria nel collo del risuonatore è

${\displaystyle m=\rho _{0}lA\;}$.

La frequenza di risonanza del sistema si può ricavare in completa analogia con la frequenza di oscillazione propria di un sistema massa-molla

${\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$.

Sostituendo i valori calcolati sopra troviamo

${\displaystyle f={\frac {v}{2\pi }}{\sqrt {\frac {A}{Vl}}}}$

Correzioni per il risuonatore reale

• Il fatto che un po' d'aria possa fuoriuscire dal recipiente durante ogni oscillazione ne aumenta di fatto la componente inerziale, e quindi comporta una correzione sensibile alla frequenza. Poiché l'effetto netto della fuoriuscita di aria è equivalente ad avere un collo leggermente più lungo, la correzione si può tradurre in una "lunghezza efficace" da usare nella formula della frequenza al posto della "lunghezza reale" del collo. La lunghezza efficace è data dalla seguente formula empirica:

${\displaystyle l'=l+{\frac {4}{5}}{\sqrt {A}}}$

Una correzione all'estremità quantitativamente differente, ma concettualmente identica si deve applicare anche a tutti gli strumenti a fiato reali.

• La presenza di attrito viscoso, invece, ha un effetto piuttosto piccolo sulla frequenza di risonanza, che, come in tutti i sistemi oscillanti, dipende solo dal bilancio tra le componenti inerziali e quelle elastiche del sistema. L'attrito ha solo effetto sul fattore di merito del sistema, e cioè sulla larghezza della risonanza (si veda la discussione nella pagina sulla risonanza in generale). La presenza di attrito, insieme al piccolo scambio di aria tra l'esterno e l'interno, giustifica il fatto che, una volta eccitata, la vibrazione si smorza dopo un certo tempo, a meno che ulteriore energia non venga fornita continuamente dall'esterno. Inoltre, maggiori sono gli attriti maggiore sarà l'intervallo di frequenze in cui il risuonatore risponde. In presenza di grandi attriti il risuonatore è meno selettivo in frequenza.
• Assai diverso invece è il ruolo dell'attrito e del moto turbolento per quanto riguarda la "messa in vibrazione" del risuonatore. Infatti, oltre che "rispondere" ad una sorgente sonora esterna per risonanza, il risuonatore di Helmholtz può essere eccitato soffiando contro un bordo dell'imboccatura. Per maggiori dettagli su come un flusso continuo di aria possa trasformarsi in un onda di pressione oscillante si vedano le pagine su flauto e fischietto e ocarina.

Simulazione della risposta

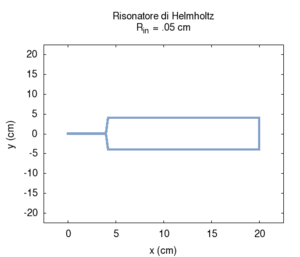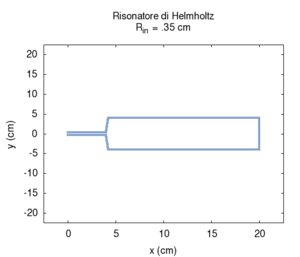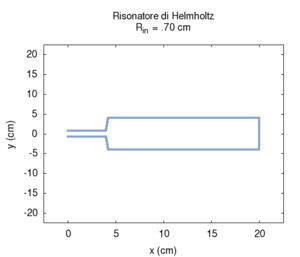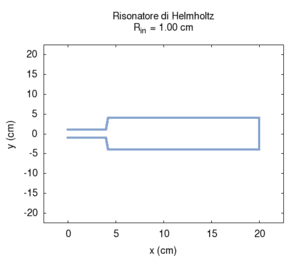
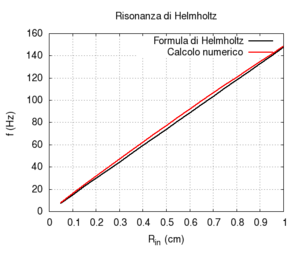
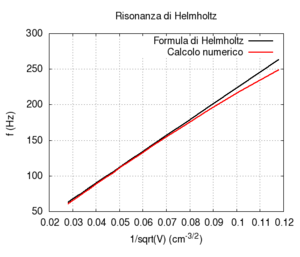
Abbiamo effettuato una simulazione della risposta di un risuonatore di Helmholtz cilindrico, e abbiamo paragonato i risultati numerici con la formula di Helmholtz discussa nel paragrafo precedente. Osserviamo solo piccole deviazioni dai valori predetti da Helmholtz, una volta che la lunghezza dell'imboccatura sia corretta per tenere conto della fuoriuscita d'aria. Ricordiamo che la formula vale solo quando il volume della cavità è molto maggiore del volume dell'imboccatura, mentre la correzione di lunghezza efficace è solo un'approssimazione elementare. Naturalmente per grandi dimensioni della bocca l'effetto della radiazione diviene più importante, mentre per piccole sezioni bisognerebbe tenere conto degli effetti dell'attrito viscoso, nella simulazione di un risuonatore reale. Non abbiamo tenuto conto di questi effetti in questa sede.

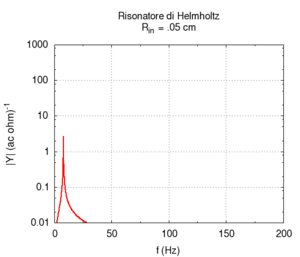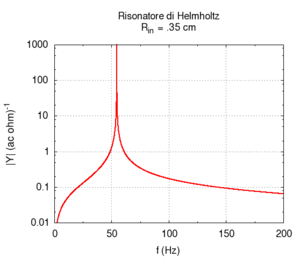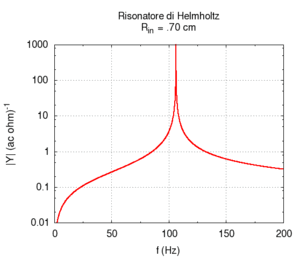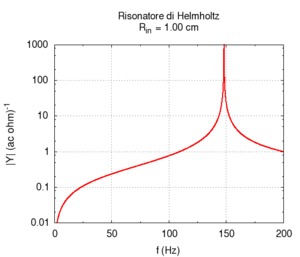
Abbiamo prima studiato la dipendenza della frequenza di risonanza dalla sezione dell'imboccatura. Contrariamente a quanto ci si potrebbe aspettare, ma in accordo con quanto previsto da Helmholtz, la frequenza aumenta man mano che si allarga la sezione dell'imboccatura.

Geometria	Risposta acustica	Risonanze

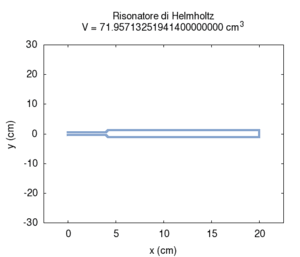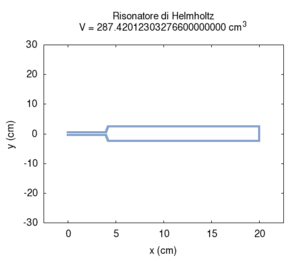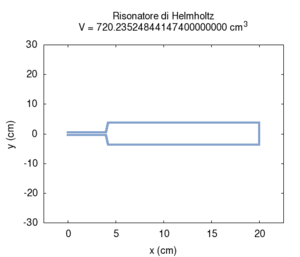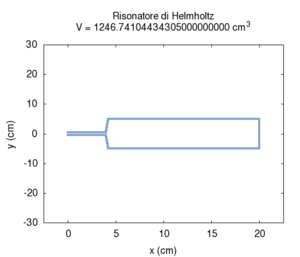
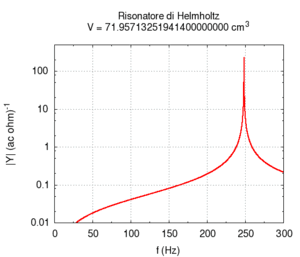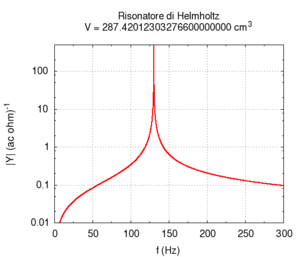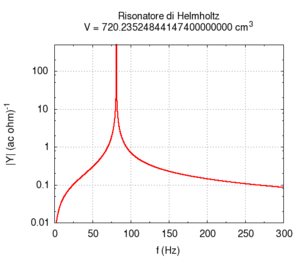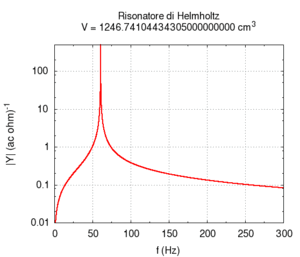
Il secondo effetto è più noto: all'aumentare del volume del risuonatore la sua frequenza di risonanza diviene più grave. Questo determina la caratteristica struttura dei banchi di risonatori, utilizzati una volta come filtri, in lunghe file di dimensioni progressivamente crescenti. Questa struttura è in realtà caratteristica di tutti gli strumenti musicali che producono suoni basandosi su banchi di risuonatori, come il pianoforte, l'organo o (anche se in un senso più approssimativo) l'intera orchestra. Nel calcolo si nota che l'errore maggiore nel calcolo numerico si ha per grandi dimensioni trasversali della cavità. Questo errore è principalmente da attribuirsi all'assunzione semplificatrice che le onde stazionarie nella cavità si possano instaurare solo lungo l'asse del cilindro.

Geometria	Risposta acustica	Risonanze

Approfondimenti e collegamenti

• Altre pagine sono dedicate ad ulteriori notizie sulle cavità risonanti, e al ruolo della risonanza negli strumenti musicali.
• Si veda la pagina su fischietto e ocarina, che sono i soli strumenti in cui il suono sia interamente determinato dalla risonanza di Helmholtz.
• Il Teorema di Fourier fornisce la base matematica rigorosa per la scomposizione di un suono in suoni puri.
• Utilizzando il nostro applet nel laboratorio virtuale puoi disegnare la tua onda sonora, analizzarne le frequenze componenti, sentire il suono corrispondente e modificarlo a piacere.

---