Enunciato e applicazioni del Teorema di Fourier

• Il teorema di Fourier afferma che

qualunque funzione periodica di periodo ${\displaystyle T_{0}}$ o, che è lo stesso, di frequenza ${\displaystyle f_{0}=1/T_{0}}$, continua e limitata può essere rappresentata mediante una somma di funzioni sinusoidali pure di opportuna ampiezza e di frequenza multipla della frequenza fondamentale ${\displaystyle f_{0}}$.

• Nella sezione onde armoniche, che ti invitiamo a rileggere prima di affrontare questa impegnativa pagina, abbiamo descritto un tipo particolare di oscillazione detta armonica, descritta da una particolare funzione periodica detta seno.
• Nella pagina sul moto armonico è mostrato che molte delle oscillazioni presenti in natura sono correttamente descritte da tale funzione periodica.
• In questa pagina imparerai che l'oscillazione armonica descritta dalla funzione sinusoidale è addirittura una sorta di oscillazione periodica fondamentale con la quale "costruire", in un senso da precisare, tutti i tipi di oscillazione periodici e non. Questa affermazione si basa su di un noto (per gli addetti ai lavori) teorema matematico dovuto al fisico matematico francese Fourier.
• La costruzione di una qualunque oscillazione complessa a partire dalla sovrapposizione di oscillazioni armoniche semplici costituisce un procedimento detto sintesi che viene largamente impiegato nella produzione di apparati elettronici capaci di riprodurre il timbro dei vari strumenti musicali o di produrre suoni del tutto artificiali (si pensi alle sonorità, inaudite ed irrealizzabili dagli usuali strumenti musicali, di certa musica elettronica).
• La possibilità di "decomporre" l'oscillazione complessa nelle sue oscillazioni armoniche costituisce, per così dire, il procedimento inverso della sintesi e viene denominato analisi spettrale o analisi di Fourier. Tale analisi, ben lungi dall'essere una mera curiosità matematica, offre la base teorica per innumerevoli applicazioni. Su di essa si basano
  • la possibilità di comprendere la nascita del timbro peculiare di ogni strumento musicale;
  • la progettazione di sistemi di riconoscimento e sintesi vocale;
  • la possibilità di ricercare le frequenze di risonanza dei sistemi oscillanti;
  • la maggior parte delle tecniche spettroscopiche in fisica: la parola stessa spettro si riferisce per lo più all'analisi di Fourier di un segnale. Per esempio la spettroscopia ottica è utilizzata nell'analisi chimico-fisica delle sostanze, o, in astronomia, come strumento di indagine dello spazio e dei corpi celesti. L'analisi di spettro può essere condotta anche su onde elettromagnetiche invisibili come quelle nelle bande dei raggi ultravioletti, dei raggi X, o, all'altra estremità dello spettro, delle onde radio.

Analizzatori di spettro

L'analisi spettrale, cioè la determinazione dei coefficienti ${\displaystyle a_{n}}$ e ${\displaystyle b_{n}}$, può essere effettuata anche per oscillazioni periodiche non descritte da una funzione di cui non si conosce l'espressione analitica ${\displaystyle y(t)}$. Tali oscillazioni possono essere ad esempio

• le oscillazioni di un qualunque sistema meccanico, come una corda o di una membrana di uno strumento musicale, o un ponte o un edificio sottoposto a sollecitazioni esterne;
• le oscillazioni elettriche di un circuito investito da un segnale elettromagnetico complesso, ecc.

In tali casi l'analisi spettrale viene effettuata "empiricamente" facendo interagire l'onda in questione con sistemi fisici in grado di attivare meccanismi capaci di selezionarne e discriminare, separandole, le varie componenti spettrali (cioè le varie armoniche) da cui è l'onda è costituita. Tali meccanismi possono essere di vario tipo:

• nel fenomeno della rifrazione e della dispersione il meccanismo selettivo è dato dalla dipendenza della velocità di propagazione delle varie armoniche dalla frequenze delle armoniche stesse. Nella famosissima esperienza del prisma, Newton ha scomposto la luce solare "bianca" in un fascio di raggi colorati riproducenti i colori dell'arcobaleno. Nel caso di un'onda elettromagnetica complessa, le componenti armoniche si dicono, non a caso, monocromatiche;
• nel fenomeno della risonanza il meccanismo selettivo è fornito dalla proprietà dei sistemi oscillanti di assorbire energia dalle diverse armoniche in modo più o meno efficiente.
  • Nel caso delle onde sonore, Helmholtz utilizzò tale principio per costruire un insieme di risonatori per analizzare il suono complesso generato dagli strumenti musicali. L'equivalente monocromatico del suono è un onda sonora costituita da un'unica armonica come, in prima approssimazione, quello del diapason. Oggi giorno esistono sistemi elettronici in cui la frequenza di risonanza è fissata modificando parametri fisici sui quali si ha un controllo superiore rispetto ai risonatori "meccanici" di Helmholtz. Per tale ragione l'analisi spettrale viene oggi effettuata tramite circuiti oscillanti molto più affidabili, selettivi e precisi dei risonatori di Helmholtz. Sembra che anche il nostro orecchio sia un raffinatissimo analizzatore di spettro: esso discrimina le varie armoniche facendo vibrare parti differenti, in relazione alla frequenza, della membrana basilare della coclea.
  • Nel caso delle onde elettromagnetiche i circuiti oscillanti trovano applicazioni negli apparati riceventi (radio, TV, ecc.). Infatti è evidente che quando un circuito oscillante viene investito da un'oscillazione complessa, cioè non da una singola oscillazione sinusoidale di frequenza f, ma dalla sovrapposizione di più oscillazioni, l'effetto della risonanza è quello di selezionare le frequenze prossime a ${\displaystyle f_{0}}$, attenuando tutte le altre.

Rappresentazione delle onde periodiche nel dominio della frequenza

Il teorema di Fourier ci fornisce uno strumento formidabile per una rappresentazione sintetica delle funzioni periodiche: anziché disegnare il grafico della funzione periodica è più efficace rappresentarne direttamente il contenuto spettrale mediante spettrogrammi cioè tramite un sistema di assi cartesiani avente in ascissa le frequenze delle armoniche (tutte multiple della frequenza della fondamentale) e in ordinata l'ampiezza di ciascuna armonica.

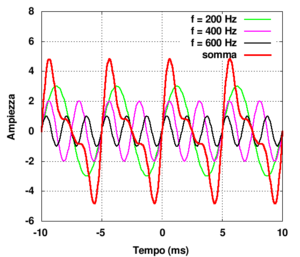
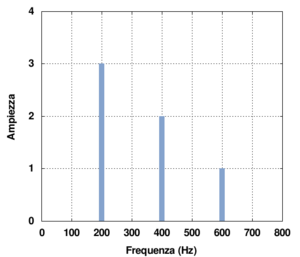
Nella figura sono rappresentati il grafico e il contenuto spettrale della funzione di equazione:

${\displaystyle y(t)=3\cdot \sin(400\pi t)+2\cdot \sin(800\pi t)+\sin(1200\pi t)}$

costituita dalla sovrapposizione (somma) di tre parziali armoniche di ampiezza (in cm) 3,2,1 e frequenza 200, 400, 600 Hz nell'ordine. Il grafico è stato disegnato per un intervallo di periodicità della funzione y(t) che è pari a T = 5 ms cioè frequenza pari a 200 Hz (che è quella della fondamentale).

Grafico nel dominio del tempo	Grafico nel dominio delle frequenze (spettro)

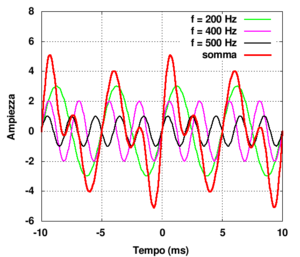
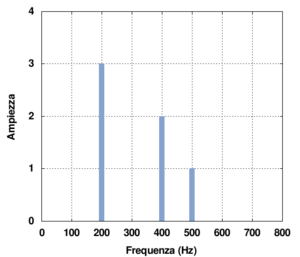
Di seguito sono riportati il grafico della funzione ed il relativo spettrogramma

${\displaystyle y(t)=3\cdot \sin(400\pi t)+2\cdot \sin(800\pi t)+1\cdot \sin(1000\pi t)}$

costituita dalla sovrapposizione (somma) di tre parziali armoniche di ampiezza (in cm) 3,2,1 e frequenza 200, 400, 500 Hz nell'ordine. (Tale forma d'onda potrebbe essere ottenuta da una funzione periodica di frequenza 100 Hz in cui è stata soppressa la prima, la quarta armonica e tutte le armoniche successive alla quinta)

Grafico nel dominio del tempo	Grafico nel dominio delle frequenze (spettro)

Anche in questo caso, il grafico è stato disegnato per un intervallo di periodicità della funzione y(t) che è pari stavolta a T = 10 ms cioè frequenza pari a 100 Hz (che è quella della fondamentale soppressa). La regola generale è che la frequenza del segnale risultante, è il massimo comune divisore (eventualmente razionale), delle frequenze delle varie armoniche. Tale fatto ha una grandissima importanza nella percezione dell'altezza di un suono nel fenomeno dell'altezza virtuale.

Alcune osservazioni

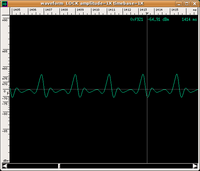
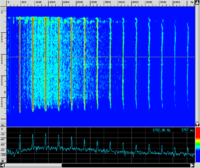
• È proprio grazie al teorema di Fourier (che ci assicura che le frequenze dello spettro sono tutte multiple della fondamentale) che il contenuto spettrale dell'onda periodica appare, nel dominio delle frequenze, costituito da una serie di linee verticali.L'analisi degli spettrogrammi di funzioni periodiche (quali sono, con buona approssimazione, quelli generati dagli strumenti musicali) ci permette di cogliere molte caratteristiche del suono emesso come l'altezza, intensità e il timbro. Di seguito sono riportati la forma d'onda, lo spettrogramma (e perché no?) l'audio di un suono reale (un Si♭ a 466 Hz) emesso da una tromba

forma d'onda	spettrogramma	Audio
		TR_Sib.mp3 Tromba: Sib a 466Hz;

Se vuoi imparare a leggere le molteplici informazioni contenute nei grafici precedenti visita la pagina Come si legge uno spettrogramma?

• Tale rappresentazione è comunque utile anche nel caso di funzioni non periodiche: come spiegato nella pagina relativa all'indeterminazione una funzione non periodica può essere "ricostruita" a partire da onde sinusoidali di qualsiasi frequenza. In questo caso il grafico del contenuto spettrale anziché essere rappresentato da picchi verticali netti, sarà formato da una distribuzione continua, che comunque permette di cogliere gli intervalli di frequenze che più contribuiscono alla formazione della funzione non periodica.

• Saper determinare il contenuto spettrale anche di forma d'onda non periodiche è fondamentale in quanto le onde reali (quali ad esempio il suono) non sono periodiche ed evolvono, assieme ai loro contenuti spettrali, nel tempo. Per tale motivo è spesso utile avere una rappresentazione di un insieme di spettrogrammi, rilevati in tempi successivi, per analizzare l'evoluzione del contenuto spettrale dell'onda. Tale metodo viene chiamato, per la grande utilità che esso ha nell'analisi dei suoni, sonogramma.

Il conoscere, tramite i sonogrammi, l'evoluzione nel tempo del contenuto spettrale di un suono ha grande importanza nella determinazione del timbro del suono stesso.

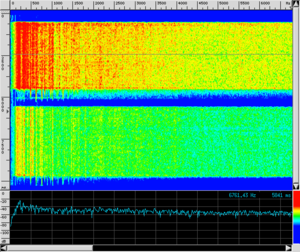
Colpo di Tam-tam: il suono cambia ad ogni istante, pur mantenendo un carattere spettrale anarmonico: non si evidenziano picchi distinti a frequenze multiple, ma un continuo distribuito su una larghezza di banda variabile nel tempo. A colpo d'occhio si distinguono però due regioni spettrali (in rosso): una attorno ai 250 Hz di larghezza circa 120 Hz, ed una più ampia da circa 600 a circa 1600 Hz.

Proposte di utilizzo dell'applet: vedi i percorsi

Per vedere il Teorema di Fourier "all'opera" può visitare l'applet relativo. L'applet è molto intuitivo e di facile utilizzo: alla pagina su il teorema di Fourier all'opera, troverai una serie di proposte per il suo utilizzo.

Collegamenti ed approfondimenti

• Se vuoi conoscere le formule per ricavare i coefficienti ${\displaystyle a_{n}}$ e ${\displaystyle b_{n}}$ visita la pagina sviluppi in serie di Fourier; troverai anche una "biblioteca" di sviluppi in serie di forme d'onda particolari (onda triangolare, onda quadra, onde a "dente di sega")
• Se vuoi vedere quanto complessa può essere un'oscillazione, visita le sezioni sintesi delle onde e modi normali in cui vedrai in quali incredibili modi può vibrare una corda fissata ai suoi estremi. Il teorema di Fourier scompone l'oscillazione complessa in sovrapposizione di oscillazioni più semplici.
• Se vuoi capire come nasce ed evolve il timbro dei suoni emessi dai vari strumenti musicali visita la pagina relativa alla percezione del timbro

---