Che cosa sono

• Ogni sistema vibrante sia esso meccanico, elettrico, o acustico, possiede particolari modi di oscillazione in cui tutte le sue parti componenti vibrano di moto armonico, e con la stessa frequenza. Questi sono appunto i modi normali del sistema.
• Quindi, ad ogni modo normale corrisponde una particolare frequenza (che si dice frequenza propria del sistema). Tuttavia non vale il viceversa: ad una stessa frequenza possono corrispondere diversi modi, in cui gli oscillatori hanno diverse relazioni di fase tra di loro. Il tipico esempio è costituito dai modi "degeneri" nelle membrane quadrate (vedi modi normali di una membrana rettangolare) e nelle risonanze acustiche di una stanza (vedi onde stazionarie in 3D).
• Ciascun modo è quindi unicamente caratterizzato
  1. dalla sua frequenza propria (o autovalore del modo), e
  2. dalle condizioni iniziali del moto per tutti gli oscillatori (o autovettore del modo).

Poiché tutti gli elementi oscillano alla stessa frequenza, gli sfasamenti reciproci si mantengono invariati durante tutto il moto.

• Di norma un sistema fisico non oscilla secondo uno solo dei suoi modi normali, ma secondo una loro combinazione (sovrapposizione). Il compito di molti dei metodi di indagine sviluppati in fisica e in ingegneria è appunto quello di identificare tutti i modi normali di un sistema.

Perché ce ne occupiamo

La grande importanza di questi modi risiede in alcune loro importanti proprietà:

1. I modi normali sono indipendenti tra di loro: l'energia totale di un sistema oscillante, comunque complesso, è semplicemente pari alla somma delle energie dei singoli modi normali che compongono l'oscillazione. L'energia che appartiene ad un particolare modo normale non viene mai ceduta ad un'altro modo. Essi sono completamente indipendenti l'uno dall'altro.
   • Si osservi che, se un sistema fisico è costituito da più oscillatori elementari, e questi si scambiano energia tra loro, il loro moto non sarà in generale un moto armonico semplice: ampiezza e frequenza del moto possono cambiare nel tempo, perché gli oscillatori componenti possono scambiarsi energia, e quindi, in ogni ostante, anche se l'energia totale resta invariata, l'energia di ciascuno dei componenti può fluttuare.
   • Se invece il sistema si trova in un suo modo normale, tutte le sue parti si comportano come fossero oscillatori indipendenti. Mantengono la loro oscillazione costante in frequenza e ampiezza, e non scambiano energia con gli altri.
   • Si veda il caso di due oscillatori accoppiati per una dimostrazione pratica e semplice di questa proprietà. #* Questa proprietà ha importanti conseguenze non solo nella meccanica classica, ma anche nella meccanica quantistica.
2. Qualunque modo di vibrazione del sistema, per quanto complicato esso sia, può essere descritto combinando opportunamente i suoi modi normali.
   • Questa affermazione non è ovvia, e la sua dimostrazione costituisce un importante teorema.
   • Si vedano anche le discussioni sul principio di sovrapposizione e sul teorema di Fourier.
3. Una volta che i modi normali siano noti, combinarli per ottenere nuove possibili oscillazioni è semplice: basta sommarli, ciascuno con una sua ampiezza e fase.
   • C'è tuttavia un rovescio della medaglia: gli "oscillatori normali" elementari possono non coincidere con gli oscillatori che fisicamente compongono il sistema. In particolare, le coordinate delle oscillazioni normali, sono, in generale, combinazioni lineari delle coordinate degli oscillatori del sistema. Si veda di nuovo il caso in cui il sistema è costituito da due soli oscillatori. Le "coordinate normali" sono in questo caso la somma e la differenza tra le oscillazioni delle singole parti.
4. I modi normali sono "semplici" anche per un altro motivo: perché tutte le parti del sistema si muovono di moto armonico semplice.
   • Di conseguenza un modo normale è definito sostanzialmente da una sola frequenza, ampiezza e fase, indipendentemente dal numero degli oscillatori elementari che compongono il sistema.
5. Le frequenze dei modi normali corrispondono alle particolari frequenze di risonanza del sistema, che indicano il modo più efficiente per scambiare energia col sistema senza disperderla.
   • Qualunque sia la natura del sistema fisico in esame, questo fatto ci consente di "vederne" chiaramente la dinamica. Nel caso di una costruzione ciò corrisponde ad evidenziarne i punti deboli. Nel caso di altri sistemi, questi potrebbero essere in realtà i punti forti (si pensi agli strumenti musicali, che producono il massimo del suono quando sono eccitati a frequenze corrispondenti a quelle di un loro modo normale).
6. Ogni differente modo in cui un sistema fisico può acquisire o cedere energia si dice grado di libertà del sistema. Poiché i modi normali sono indipendenti tra loro è evidente che il numero dei gradi di libertà di un sistema è pari al numero dei suoi modi normali.

In sintesi, lo studio dei modi normali ci permette di scomporre un moto oscillatorio, per quanto complesso sia, in componenti armoniche semplici, rivelandoci la dinamica interna del sistema.

Un esempio meccanico

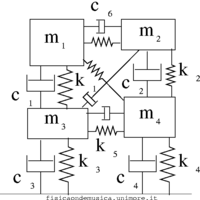
Nello schema seguente si vede:

1. a sinistra, un sistema meccanico "reale" (una casa).
2. Accanto lo schema di un suo modello matematico a base di sistemi massa-molla. A questo punto il sistema viene descritto da un insieme di proprietà (le masse m₁, m₂, ..., le costanti elastiche k₁, k₂, ... e gli attriti c₁, c₂, ...). Tuttavia, a questo livello la dinamica è intricata, e per calcolare il moto bisogna risolvere un sistema di molte equazioni accoppiate tra di loro. Non è evidente quali siano le frequenze proprie, nè cosa accada al sistema quando venga posto in risonanza con una di tali frequenze.
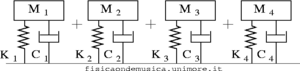
3. A destra invece è stato effettuata un'analisi modale: i modi normali sono stati individuati, e ciascuno è caratterizzato da tre costanti M_i, K_i, C_i (diverse da quelle del modello del punto precedente). Ora i modi di oscillazione del sistema sono tutti indipendenti tra di loro, e perciò possiamo predire esattamente cosa accade per ciascuna frequenza semplicemente sovrapponendo le risonanze dei modi normali.
4. La soluzione generale per una certa sollecitazione esterna sarà la sovrapposizione dei singoli moti degli oscillatori normali per quella sollecitazione.

modello fisico	modello dinamico	modi normali
L'analisi modale permette di separare un sistema composto di oscillatori accoppiati in oscillatori semplici disaccoppiati. Il moto composto è la somma dei moti degli oscillatori normali, ciascuno con la sua ampiezza e fase.

Come costruire il modello che descrive esattamente il sistema? Cioè, il che è lo stesso: come determinare i parametri M_i, K_i, C_i? Molti metodi della fisica e dell'ingegneria sono stati sviluppati per rispondere a questa domanda. La linea di pensiero è quasi sempre la stessa:

1. metodi teorici: bisogna farsi un'idea dei costituenti elementari del sistema (i singoli oscillatori) e delle loro interazioni (accoppiamenti), dedurne un sistema di equazioni che contengano i parametri, e risolverle per confrontare il moto effettivo del sistema con quello previsto teoricamente.
2. Metodi sperimentali: bisogna investigare le risonanze del sistema, il che significa tipicamente eccitare il sistema in modo opportuno e misurarne la risposta per confrontarla col modello del punto 1.

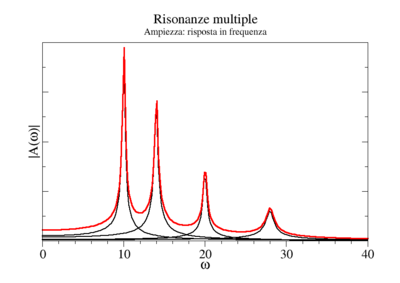
L'analisi modale evidenzia le risonanze del sistema: la risposta in frequenza del nostro modello di edificio potrebbe assomigliare a quella illustrata nella figura. La sua interpretazione è immediata: ogni picco corrisponde alla risonanza di un particolare modo normale. I quattro modi di vibrazione possono avere caratteristiche del tutto differenti, e sono determinati completamente una volta che, oltre alle frequenze proprie, sono note anche le oscillazioni degli elementi. Per es. due modi potrebbe essere di flessione, uno di torsione, ed uno di compressione. Nei tre casi l'edificio sarebbe attraversato da onde elastiche di diversa natura (flessurali, torsionali, e longitudinali), che lo solleciterebbero diversamente.

• L'applicazione in questo caso è evidente: conoscendo ad esempio che l'edificio sopporta male le torsioni, potremmo progettare uno smorzatore che inibisca il picco di torsione, rendendo la struttura più robusta in modo mirato.

Densità dei modi e dimensionalità del sistema

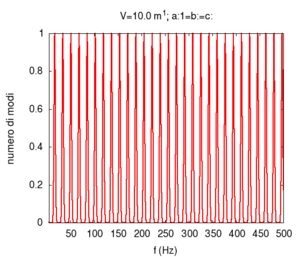
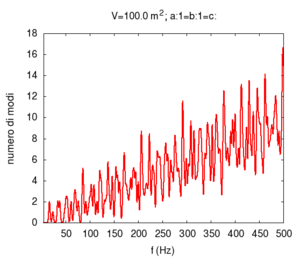
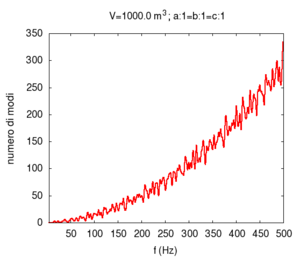
Molte proprietà dei sistemi fisici dipendono dalla distribuzione dei modi normali nello spazio delle frequenze, cioè da quanti modi esistono ad ogni data frequenza.

Ad esempio, nel caso di sistemi vibranti, è fondamentale distinguere tra sistemi in cui i modi costituiscono una distribuzione continua, da quelli in cui i modi si accumulano su certe frequenze, separate da larghi spazi non risonanti. Infatti, la risposta del sistema sarà completamente diversa. Nel primo caso avremo una risposta abbastanza omogenea a tutte le frequenze, mentre nel secondo il sistema tenderà a rispondere violentemente (cioè ad entrare in risonanza) solo in risposta a sollecitazioni mirate su frequenze precise. Se la stimolazione del sistema non avviene ad una frequenza sola, come avviene nel caso delle sollecitazioni impulsive (un colpo secco), i sistemi del secondo tipo si comporteranno come un filtro, estraendo dalla sollecitazione solo le componenti in risonanza con uno dei modi del sistema.

Anche dal punto di vista acustico la distribuzione dei modi gioca un ruolo fondamentale, e, in particolare, vogliamo sottolineare qui come alcune importanti caratteristiche del suono che è possibile estrarre da un sistema vibrante, dipendano dalla sua dimensionalità.

Parliamo qui di dimensionalità, e non di dimensione, riferendoci al fatto se il sistema sia in grado di oscillare in una, due, o tre dimensioni. Per fare un esempio fissiamo la lunghezza base del sistema a 10 m, e studiamo la distribuzione dei modi normali per un sistema unidimensionale (p. es una corda di 10 m), uno bidimensionale (una membrana di 10 m×10 m), e uno tridimensionale (una stanza di 10 m×10 m×10 m).

Sistema 1D	Sistema 2D	Sistema 3D
Questa distribuzione è caratteristica delle corde, o delle canne, e presenta una serie di picchi con frequenze in rapporti interi. Su sistemi come questi si è basata (almeno in origine) la teoria della musica occidentale. Gli strumenti corrispondenti emettono toni ben definiti e stabili. Ad ogni frequenza di risonanza corrisponde un solo modo normale. La densità dei modi rimane quindi costante.	Questa distribuzione è caratteristica di piastre o membrane. Essa può presentare notevoli variazioni della struttura a seconda del rapporto tra i lati del sistema, ma è generalmente caratterizzata dalla presenza di modi in rapporti non armonici. Gli strumenti "bidimensionali" non generano necessariamente toni di altezza definita proprio per questa ragione. Su di essi si basano maggiormente le musiche dell'est Asia.	Questa distribuzione è caratteristica degli ambienti, anche se i dettagli della sua struttura dipendono fortemente dal rapporto tra le lunghezze dei lati. Rispetto alle altre due essa presenta una maggiore densità, a parità di lunghezza dell'elemento base (10 m), e quindi, una risposta meno risonante, e più omogenea. Il numero dei modi aumenta con il quadrato della frequenza.

In conclusione osserviamo solo che l'analisi dei modi normali si riferisce solo agli stati stazionari del sistema, quelli cioè in cui le oscillazioni sono entrate a regime, e non cambiano sostanzialmente le proprie caratteristiche nel corso del tempo. Molte altre proprietà acustiche e dinamiche dei sistemi dipendono invece dai regimi transitori, che non possono essere analizzati in termini dei soli modi normali, oppure dagli effetti non lineari, che sono esaminati altrove.

Approfondimenti e collegamenti

I modi normali non sono una proprietà dei soli sistemi elastici, ma sono comuni a tutti i sistemi oscillanti, siano essi elettrici, acustici, meccanici, macroscopici (cioè descritti dalla fisica classica)o quantistici (cioè descritti dalla fisica quantistica).

• Vedi le sezioni sulla risonanza e sulle onde stazionarie per avere una visione più completa sui modi normali.
• Vedi anche le Domande e risposte sulla risonanza
• Per scoprire quale importanza hanno i modi di vibrazione degli strumenti musicali rispetto al suono che essi producono vedi la sezione sulla fisica degli strumenti musicali e le Domande e risposte sugli strumenti musicali.

Segui questi link per vedere e sentire i modi normali di alcuni oggetti vibranti, che assumono particolare importanza per gli strumenti musicali.

1. modi normali di una corda
2. modi normali di una membrana circolare
3. modi normali di una membrana rettangolare
4. oscillatori accoppiati

---