Descrizione

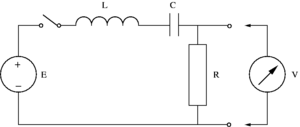
• Il circuito elettrico qui raffigurato è un semplice circuito oscillante in serie. Esso consiste di un induttore L, un condensatore C, un resistore R, un generatore di tensione E che può essere collegato al circuito, e un voltmetro V per effettuare misure di tensione.
• Il carattere oscillante del circuito è determinato dalla presenza simultanea degli elementi L e C che, collegati tra loro, sono in grado di rimbalzarsi vicendevolmente l'energia elettrica che ricevono dal generatore E. Questi due elementi sono del tutto analoghi ad una massa ed una molla, che, quando sono accoppiate, si "palleggiano" l'energia proveniente da una spinta esterna.
• Il resistore R non contribuisce all'oscillazione, ma è messo per completezza, perché qualunque circuito elettrico reale ha una componente resistiva. Nell'analogo meccanico corrisponde alla presenza di un termine di attrito, che dissipa in calore parte dell'energia che riceve.

Funzionamento

• Il circuito sopra raffigurato -detto RLC dal nome dei suoi componenti- è caratterizzato da una frequenza propria di oscillazione ${\displaystyle f_{0}}$: cioè esso è in grado di produrre una corrente oscillante in risposta ad un impulso esterno come la rapida chiusura ed apertura dell'interruttore.
• La frequenza propria ${\displaystyle f_{0}}$ costituisce la risonanza del circuito, cioè il circuito è in grado di assorbire la massima quantità di energia da un generatore esterno di tensione alternata E quando la tensione fornita dal generatore oscilla ad una frequenza molto vicina ad ${\displaystyle f_{0}}$ (si vedano anche le sezioni specifiche su risonanza e impedenza).

Cerchiamo di cogliere queste caratteristiche mediante alcuni esempi, seguendo passo-passo come avviene l'oscillazione in ciascun caso.

Oscillazioni libere

Illustriamo come si producono le oscillazioni nel circuito RLC per mezzo dell'analogia meccanica con il sistema massa-molla

Esempio di oscillazioni libere

sistema massa-molla	circuito oscillante RLC
Quando il sistema è in equilibrio la massa non si muove.	Quando il sistema è in equilibrio non circola corrente.
Immaginiamo di spostare la massa in una certa posizione fuori dall'equilibrio, e studiamo l'andamento nel tempo (moto) della velocità della massa non soggetta ad alcuna forza esterna.	Immaginiamo di accumulare una carica ad un terminale del condensatore, e, sostituito il generatore della figura con un cortocircuito, studiamo l'andamento nel tempo della corrente che attraversa il circuito libero.
inizia l'oscillazione
Quando si sposta la massa dalla posizione di equilibrio una forza di richiamo tende a riportarla verso l'equilibrio: questo mette in movimento la massa.	Quando si accumula carica ad un terminale del condensatore una differenza di potenziale tende a ridistribuire la carica nel circuito: questo produce una corrente.
Tanto maggiore è lo spostamento dall'equilibrio, tanto maggiore è la forza di richiamo (proprietà della forza elastica della molla)	Tanto maggiore è la carica accumulata sul condensatore C, tanto maggiore è la differenza di potenziale ai capi del circuito (proprietà del condensatore).
La massa, soggetta alla forza di richiamo, accelera verso la posizione di equilibrio.	Le cariche del circuito, soggette ad una differenza di potenziale, accelerano verso la condizione di equilibrio.
Raggiunto il punto di equilibrio la massa, che ha acquisito una certa velocità, continua a muoversi per inerzia oltrepassandolo.	Raggiunto il punto di equilibrio la corrente continua a fluire nel circuito per inerzia, e la carica inizia ad accumularsi sull'altro terminale del condensatore.
Dopo qualche tempo la forza di richiamo bilancia di nuovo lo spostamento. Essa ha intensità pari alla forza nell'istante iniziale, ma agisce in direzione opposta.	Dopo qualche tempo la differenza di potenziale bilancia la carica accumulata. Essa ha modulo pari alla differenza di potenziale nell'istante iniziale, ma è di segno opposto.
siamo a metà l'oscillazione: il moto continua da qui in modo simmetrico
In presenza di forze d'attrito (p. es. attrito viscoso proporzionale alla velocità del moto) le oscillazioni si smorzano esponenzialmente nel tempo	In presenza di una resistenza R (caduta di potenziale proporzionale all'intensità della corrente) le oscillazioni si smorzano esponenzialmente nel tempo
frequenza delle oscillazioni libere del sistema (frequenza propria, o naturale, o di risonanza)
${\displaystyle f_{0}={\frac {1}{2\pi }}{\sqrt {\frac {k}{M}}}}$	${\displaystyle f_{0}={\frac {1}{2\pi {\sqrt {LC}}}}}$

Come già osservato, nella definizione della frequenza propria del sistema intervengono solo due parametri: l'inerzia dell'oscillatore (massa M, o induttanza L), e la costante della forza di richiamo (costante elastica k, o inverso della capacità elettrica C). Il bilancio tra queste due grandezze produce il comportamento oscillatorio, sotto opportune condizioni iniziali.

Oscillazione e trasformazione dell'energia

Da un altro punto di vista potremmo descrivere l'oscillazione come la trasformazione dell'energia che avviene periodicamente da una forma ad un'altra.

sistema massa-molla	circuito oscillante RLC
La massa è ferma quando si trova nel punto di massima ampiezza dell'oscillazione. In questo istante l'energia del sistema è tutta energia potenziale della molla.	Nel circuito non circola corrente quando il condensatore è carico al limite della sua capacità. In questo istante l'energia del sistema è tutta energia potenziale elettrostatica dovuta alla differenza di potenziale tra i terminali del condensatore.
La massa si muove con velocità massima quando passa per il punto di equilibrio. In questo istante l'energia del sistema è tutta energia cinetica dovuta al moto della massa.	La corrente che circola nel circuito è massima quando il condensatore è scarico. In questo istante l'energia del sistema è tutta energia di induzione magnetica dovuta alla corrente che circola nell'induttanza L.

Oscillazioni forzate

Ora studiamo cosa accade quando, anziché lasciare libero il circuito di oscillare, lo forziamo ad oscillare dall'esterno partendo dalla condizione di equilibrio, e collegando il circuito ad un generatore di corrente sinusoidale ad una frequenza f.

• Sostanzialmente quello che stiamo facendo è incanalare energia proveniente dal generatore esterno nell'oscillatore. Ma energia in che forma? Questo dipende istante per istante dallo stato del generatore, e quindi dalla sua frequenza f.
• Tuttavia il sistema oscillante reagisce secondo la propria dinamica, e cioè, nel tempo, immagazzina l'energia in una forma che dipende dalla propria frequenza naturale ${\displaystyle f_{0}}$. Infatti, poiché il sistema ha una "inerzia" propria, serve un certo tempo perché l'energia si trasformi da potenziale a cinetica (o da elettrica in magnetica), e l'oscillazione si compia.
• Quindi il trasferimento di energia dal generatore all'oscillatore è tanto più efficace quanto più la frequenza del generatore è vicina alla frequenza propria dell'oscillatore, perché solo in questo modo generatore e circuito non si ostacolano a vicenda.
• Quando ${\displaystyle f=f_{0}}$ si dice che il generatore e l'oscillatore sono in risonanza.
• In questa condizione il generatore fornisce energia al circuito ad ogni oscillazione. In assenza di resistenze l'ampiezza delle oscillazioni diverrebbe infinita. In realtà, anche se gran parte dell'energia del generatore serve a mantenere le oscillazioni, una parte viene dissipata, e le oscillazioni raggiungono un valore massimo finito. L'effetto della resistenza consiste quindi nel rendere la risonanza meno forte, ma anche nell'addolcire la condizione di risonanza, infatti, se il sistema dissipa energia, anche frequenze non esattamente identiche a f₀, ma comprese in un intervallo f₀± Δf saranno "in risonanza".
• Quando la frequenza del generatore è molto diversa dalla frequenza propria del sistema, l'azione del generatore ostacola l'oscillazione libera del circuito, e le oscillazioni risultanti sono piccole. La maggior parte dell'energia viene dissipata, anziché trasferirsi al circuito.

Nota bene:

1. Se la corrente prodotta dal generatore oscilla come una sinusoide, anche la corrente che attraversa il circuito oscilla come una sinusoide. Questa è una proprietà fondamentale del moto armonico.
2. In generale le oscillazioni del sistema e della sorgente di energia (il generatore) non avvengono con la stessa fase, cioè, ad esempio, la massima ampiezza dell'oscillazione non è raggiunta nello stesso istante. L'entità dello sfasamento dipende dalla frequenza dell'oscillatore.

Ricordiamo che le due proprietà del sistema che determinano il comportamento oscillatorio sono in realtà in competizione tra loro per "aggiudicarsi" l'energia. Poiché l'energia disponibile ad ogni istante è finita, quando l'energia è massima in una forma deve essere minima nell'altra. Questo spiega qualitativamente perché l'energia debba venir fornita dall'esterno in modo "mirato", e cioè al momento giusto. È facile comprendere come rinforzare o ostacolare l'oscillazione se consideriamo un particolare generatore periodico che, anziché fornire energia come una sinusoide, fornisce impulsi ad intervalli regolari. Eccone l'esempio

Esempio di oscillazioni forzate

sistema massa-molla	circuito oscillante RLC
Il generatore fornisce una forza diretta verso il punto di equilibrio (si pensi al sistema massa-molla come ad un'altalena, e al generatore come una persona che dà delle spinte ritmiche sempre nello stesso verso)	Il generatore fornisce una differenza di potenziale sempre della stessa polarità (si pensi ad una batteria che viene connessa e disconnessa ad intervalli regolari tramite un interruttore)
in risonanza (f=f0)
La massa è spinta ogni volta che si trova in uno solo dei punti di massima ampiezza dell'oscillazione (p. es. quando la massa è nell'estremo destro dell'oscillazione)	La batteria viene connessa nel momento in cui il condensatore è completamente carico con polarità concorde a quella dei terminali della batteria (cioè il polo + della batteria è dalla stessa parte del terminale del condensatore a carica positiva)
Ogni volta che la massa raggiunge il punto prefissato ha velocità nulla, e accelerazione massima diretta verso il punto di equilibrio. La forza applicata aumenta questa accelerazione di una stessa quantità ad ogni periodo.	Ogni volta che il condensatore è carico, un'ulteriore carica è portata dal generatore, e quindi l'intensità della corrente nel momento della scarica diviene sempre maggiore ad ogni periodo.
fuori risonanza (f=2f0)
La massa è spinta ogni volta che si trova in uno qualsiasi dei punti di massima ampiezza dell'oscillazione (cioè sia all'estremo destro sia all'estremo sinistro), ma la forza applicata è diretta in entrambi i casi nello stesso verso	La batteria viene connessa nel momento in cui il condensatore è completamente carico con qualunque polarità (cioè il polo + della batteria è una volta dalla stessa parte del terminale del condensatore a carica positiva, e una volta dalla parte del terminale a carica negativa)
Una volta su due la spinta aumenta l'accelerazione, e una volta la diminuisce. Ne risulta una ampiezza di oscillazione minore rispetto al caso in risonanza.	Una volta su due la carica del condensatore aumenta, e una volta diminuisce. Ne risulta una carica totale complessivamente minore rispetto al caso in risonanza.

Osservazioni e approfondimenti

• Il modello che questo circuito rappresenta si può applicare per descrivere i sistemi fisici più diversi tramite lo strumento dell'analogia fisica. Per esempio, lo stesso modello descrive molto bene, da un punto di vista macroscopico (cioè senza dover ricorrere ad una teoria atomica), il comportamento dei cristalli piezoelettrici, che si utilizzano come oscillatori di precisione negli orologi "al quarzo", o nella circuiteria di sincronizzazione dei moderni televisori, con frequenze comprese tra i 5 kHz e i 50 MHz.
• Con l'avvento dell'elettronica digitale molti dei circuiti oscillanti analogici come quello sopra descritto sono stati sostituiti da circuiti basati su transistor o amplificatori operazionali. Inoltre spesso la forma dell'oscillazione utilizzata è un'onda quadra, anziché una sinusoide. Tale è, ad esempio, il clock delle CPU nei microprocessori. Tuttavia le idee generali sulla fisica dell'oscillazione sono già completamente contenute nel prototipo analogico qui descritto, che ha costituito per decenni il componente base degli apparecchi di ricezione e trasmissione radio.
• Dal punto di vista tecnologico i circuiti oscillanti trovano applicazioni molteplici, specialmente come filtri negli HiFi, e circuiti accordati negli apparati riceventi (radio, TV, ecc.). Infatti è evidente che quando un circuito tipo RLC è investito da un'oscillazione complessa, cioè non da una singola oscillazione sinusoidale di frequenza f, ma dalla sovrapposizione di più oscillazioni, l'effetto della risonanza è quello di selezionare le frequenze prossime a ${\displaystyle f_{0}}$, attenuando tutte le altre.
• Sfruttando il fatto che la frequenza di risonanza del circuito può essere regolata variando uno dei suoi parametri, come la capacità C, ecco che abbiamo un'idea di come funziona il sintonizzatore di una radio (la manopola che, girando, seleziona il canale, in genere è proprio un condensatore a capacità variabile).

---