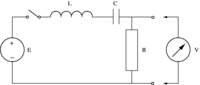
Filtri
Da "Fisica, onde Musica": un sito web su fisica delle onde e del suono, acustica degli strumenti musicali, scale musicali, armonia e musica.
Jump to navigation Jump to searchGeneralmente parlando un filtro è un dispositivo che riceve in ingresso un segnale contenente un certo insieme di frequenze, e ne restituisce in uscita un altro contenente solo frequenze appartenenti ad un sottoinsieme delle frequenze in ingresso. In particolare, il filtro si chiama
- passa-alto se lascia passare tutte le frequenze maggiori di una data frequenza detta di taglio
- passa-basso se lascia passare tutte le frequenze minori di una data frequenza detta di taglio
- passa-banda se lascia passare tutte e sole le frequenze in un intorno di una data frequenza detta di risonanza
- elimina-banda se blocca tutte e sole le frequenze in un intorno di una data frequenza detta di risonanza
Il concetto si chiarisce subito tramite alcuni esempi:
- Un vetro colorato è un filtro ottico: riceve in ingresso luce bianca (cioè composta da tutte le frequenze visibili), e restituisce in uscita solo frequenze corrispondenti al colore del vetro. L'energia del segnale in ingresso corrispondente alle frequenze "fermate" dal vetro resta nel vetro, e si trasforma in calore.
- Un filtro meccanico può essere costituito nella sua forma più semplice, da un oscillatore armonico. L'oscillatore riceve una forza esterna, e la trasmette ad un altro sistema meccanico. Tuttavia, se si forza l'oscillatore a vibrare ad una frequenza lontana dalla propria risonanza l'oscillatore si comporta sostanzialmente come un connettore rigido, trasmettendo efficacemente tutta l'energia ricevuta al sistema finale, mentre, in prossimità della risonanza, esso stesso tenderà a mettersi in forte oscillazione, disperdendo il lavoro effettuato dalla forza motrice esterna sotto forma di calore. Lavorando in risonanza l'oscillatore può quindi filtrare forze esterne in un certo intervallo di frequenza (per i dettagli si veda la pagina sulla risonanza negli edifici).
- Un semplice tubo costituisce un filtro acustico di tipo passa-alto. Infatti l'onda sonora che lo percorre subisce riflessione e interferenza solo in direzione radiale, mentre longitudinalmente al tubo essa può propagarsi liberamente. Queste condizioni al contorno determinano la frequenza di taglio della guida.
La funzione di un filtro, quindi, consiste nel selezionare e nel lasciar passare indisturbate alcune particolari frequenze, attenuando tutte le altre. Non ci vogliamo addentrare qui nella descrizione dei diversi possibili filtri, ma piuttosto mostrare che, grazie all'uso dell'analogia fisica, e del concetto di impedenza, il funzionamento dei filtri, di qualunque genere essi siano (elettrico, meccanico, acustico), può essere compreso in modo unitario.
Il filtro passabanda
Questo tipo di filtro è sostanzialmente composto da un sistema risonante. La risonanza, ricordiamo, è la proprietà del sistema di assorbire energia solo in un particolare ambito di frequenze, detto banda passante, accoppiandosi invece molto debolmente alle frequenze al di fuori di esso.
Questa proprietà è particolarmente utile quando si vogliono costruire dispositivi in grado di isolare un sistema fisico da un disturbo esterno, come, ad esempio, un edificio dalle scosse di terremoto, o un circuito elettrico dall'influenza di altri circuiti o di anomalie elettromagnetiche. Vista in senso complementare la funzione del filtro è quella di accoppiarsi fortemente con un segnale ad una data frequenza (o meglio con tutte le frequenze all'interno della banda passante), come accade quando si sintonizza una radio. La sintonia è infatti ottenuta modificando la frequenza di risonanza del ricevitore in modo che il centro banda cada alla frequenza della stazione che si vuole ricevere, eliminando i segnali di tutte le altre stazioni. Questi esempi sono meglio illustrati alle relative pagine risonanza negli edifici, circuiti oscillanti, radio.
In modo grafico possiamo immaginare il processo come segue:
| input frequenze | filtro passa-banda | output frequenze |
|---|---|---|
|
|

|
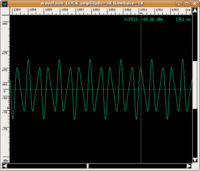
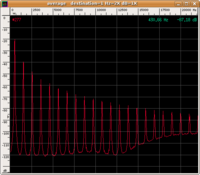
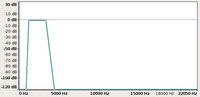
| Il segnale in ingresso contiene molte diverse frequenze | Nel dominio della frequenza il filtro corrisponde ad un profilo di impedenza o, più spesso al suo inverso (ammettenza) | Il segnale all'uscita del filtro si ottiene moltiplicando il segnale in ingresso per l'impedenza si ottiene |
Si noti che, finché si ragiona in termini di frequenze (si dice che si lavora nello spazio di Fourier), l'azione del filtro è matematicamente descritta da una semplice moltiplicazione tra le frequenze in ingresso, e l'impedenza del filtro per ogni frequenza.
Nello spazio reale, ovvero nel dominio del tempo, le cose sono un poco più complicate. Infatti, se il segnale in ingresso contiene più frequenze, significa che non ha forma di sinusoide, e, siccome le diverse componenti spettrali del segnale sono attenuate in modo diverso, il segnale in uscita non avrà più la stessa forma che aveva in ingresso.
Anche se matematicamente è più semplice descrivere l'azione del filtro nel dominio delle frequenze, noi viviamo nello spazio reale, e quindi l'effetto di un filtro passabanda ci si manifesta sempre come un cambiamento nella forma spaziotemporale del segnale. In acustica, per esempio, questa forma è collegata alla proprietà del suono percepito che chiamiamo timbro (si veda percezione del timbro). Eccone alcuni esempi
| input | filtro passa-alto | output | ||
|---|---|---|---|---|
| forma d'onda |
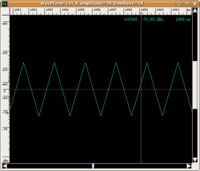
|
|
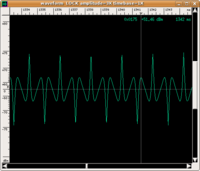
|
|
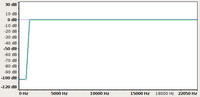
| spettro |

|
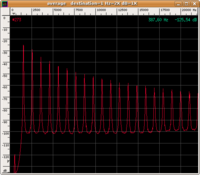
|
||
| suono |
|
|
| input | filtro passa-basso | output | ||
|---|---|---|---|---|
| forma d'onda |

|
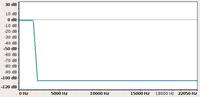
|
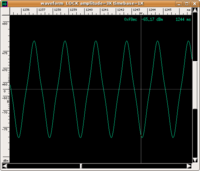
|
|
| spettro |

|
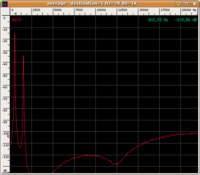
|
||
| suono |
|
|
| input | filtro elimina-banda | output | ||
|---|---|---|---|---|
| forma d'onda |

|
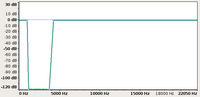
|
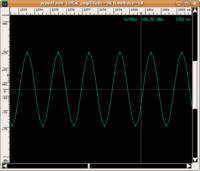
|
|
| spettro |

|
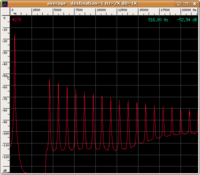
|
||
| suono |
|
|
Filtri passabanda per il suono
- Un esempio da manuale è costituito dai Risuonatori di Helmholtz. Essi sono cavità risonanti, con banda piuttosto stretta, se sono di buona qualità, ed infatti ciascuno di essi ha la proprietà di selezionare una particolare frequenza e di "estrarla" così dal suono complessivo che li investe. Un banco di risuonatori accordati alle diverse frequenze costituisce perciò uno strumento rudimentale di analisi di Fourier del suono.
- Ancora, il nostro orecchio funziona apparentemente come un banco di risuonatori (si veda fisiologia del sistema uditivo e percezione dell'altezza). La coclea, infatti, cioè l'ultima parte dell'orecchio interno in cui il suono si trova ancora come onda meccanica, prima di essere trasformato in impulso elettrico, è una guida d'onda a sezione conica, si comporta effettivamente come una serie di filtri passabanda con bande adiacenti, ed è in grado di distribuire l'energia sonora nello spazio reale in funzione dell'energia presente in ogni banda nello spazio di Fourier.
- Moltissimi strumenti musicali possono essere descritti da un modello sorgente-filtro: una sorgente di oscillazioni produce una vibrazione complessa, che contiene molte frequenze. L'oscillazione della sorgente viene forzata ad attraversare un filtro (in genere molto complesso, composto da molti diversi passabanda), che determina la qualità del suono irradiato dallo strumento. Per esempio:
- negli archi, come il violino la sorgente sono le corde. Esse, eccitate dall'arco, producono un'onda "a dente di sega", che viene trasmessa al corpo dello strumento che la irradia nell'aria. Il filtro (e adattatore di impedenza) è costituito da tutte le parti che costituiscono il corpo di legno dello strumento.
- nei fiati ad ancia, come l'oboe o il clarinetto, l'esecutore soffia attraverso un'ancia, che produce un suono piuttosto aspro. La vibrazione dell'ancia è poi filtrata dal corpo dello strumento, costituito da una guida d'onda (cilindrica o conica, o di forma composita), che ne determina l'altezza (attraverso i fori), e il timbro.
- in altri fiati, come il flauto o la tromba, l'oscillazione dell'aria non è prodotta dalla vibrazione di un ancia, ma il principio del filtro si applica allo stesso modo. Infatti l'imboccatura dello strumento da sola non è in grado di modulare l'altezza del suono, né produce un timbro paragonabile a quello dello strumento completo.
Per ulteriori approfondimenti si veda la pagina suono e risonanza, e le pagine dei singoli strumenti
| input | filtro a tre poli | output | ||
|---|---|---|---|---|
| forma d'onda |

|
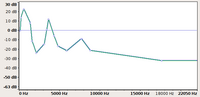
|
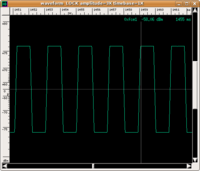
|
|
| spettro |

|
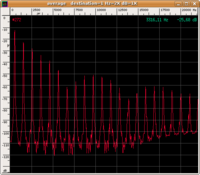
|
||
| suono |
|
|
Collegamenti e approfondimenti
L'effetto dei filtri si può sperimentare in modo interattivo nell'Applet Onde 2D. Diversi percorsi che guidano le esperienze sono disponibili ai seguenti paragrafi:
Molti concetti qui solamente citati trovano illustrazione più accurata alle pagine
Per esempi più dettagliati dell'azione dei filtro in vari contesti si veda
- Esempi di fenomeni di risonanza
- Suono e risonanza
- Guide d'onda e approfondimenti sulle guide d'onda
- i vari strumenti musicali