What are beats

We will start with an electronically generated sample of two base sounds, which are two pure sounds (i.e. with a sinusoidal wave shape) at 40 and 50 Hz. These sounds are located at the lower end of the audible spectrum and are usually filtered out by speakers; therefore, you will need to use headphones to hear them.

When we listen to the two sounds together, examining the sonogram allows us to verify that the only two frequencies present are actually at 40 and 50 Hz. However, you will note that you do not hear two distinct sounds, as you would expect, but a single sound of intermediary pitch with a distinct "beat". You can verify directly on the wave plot using the time scale that the oscillation has a period of about 22 ms, which corresponds to the sound we hear, while the distance between the two consecutive absolute maxima is 100 ms, which corresponds to the "beat" frequency (10 Hz).

Pure component sounds
Puro_40Hz.mp3 Pure sound at 40 Hz	Puro_50Hz.mp3 Pure sound at 50 Hz
NOTE: these sounds are only audible with headphones or Hi-Fi speakers and not with small PC speakers.

Sound composed by overlapping pure sounds
Wave shape	Sonogram	Audio
		Battimenti_40_50.mp3 Beats between two pure sounds at 40 and 50 Hz

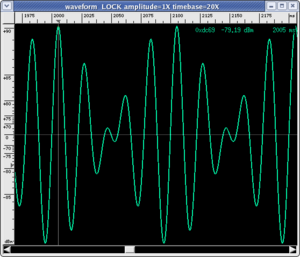
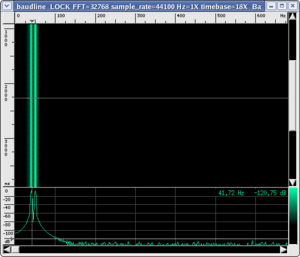
Technically, beats are produced by the superposition of two sinusoidal waves having the same pitch and "slightly different" frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$. The resulting wave has a characteristic shape that exhibits a type of "double oscillation":

1. a rapid frequency oscillation ${\displaystyle f_{0}}$ equal to the average value of the two frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ (obviously, with ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ being very close, ${\displaystyle f_{0}}$ will be equal to about ${\displaystyle f_{1}}$);
2. a much slower oscillation that "modulates" the pitch with a beat frequency ${\displaystyle f_{b}}$ equal to the difference of the two frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ (obviously, with ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ being very close, ${\displaystyle f_{b}}$ will be much less than the two frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$.

At first glance, it would appear that the beats are simply a manifestation of the superposition principle: by adding two waves, a new wave with different characteristics is obtained. This is not so. The "beat" phenomenon fully manifests its importance only in the field of acoustics. This explains the name of the phenomenon itself, which is due to the slow fluctuation of perceived intensity which makes sound seem to have a regular pulsation.

In the case of sound waves, our auditory system perceives the superposition of two sounds very differently depending on the distance between the frequencies of the component sounds. In particular:

• if the frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ are sufficiently far apart, the superposition of the two sounds is perceived as the blending of "two distinct voices".
• however, if the frequencies ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ are very close, we do not perceive two distinct voices but a single "beating" sound with a pitch close to the pitches of the components.

We will not specify here what "close" and "far" frequencies mean, we will just present several examples. For a full explanation, visit the pages on Perception of pitch and Critical bands.

How do we calculate beat frequency?

Without getting too deep into mathematical details, it is easy to understand why phenomena that repeat with very similar periodicity can give rise to an overall periodic phenomenon (the superposition of two waves) that has a longer duration in time. As with our illustrious predecessors,^[1] we can refer to a similar case: let's suppose we have two pendulums, the first oscillates at 40 times per second (corresponding to a frequency of 40 Hz) and the second at 50 times per second.

If, at the moment ${\displaystyle t=0}$, the pendulums are exactly in phase (i.e. they are at the highest point in the oscillation at the same time), how long will it take for this coincidence to occur again?

The first pendulum takes 1/40 of a second (equal to 25 milliseconds or ms) to complete an oscillation, the second pendulum takes 1/50 of a second (equal to 20 ms). The coincidence will re-occur after a time period that is the least common multiple of the two individual oscillation times, which in this case is 100 milliseconds, as you can see in the following figure. Therefore, the phenomenon of simultaneously being at the highest point will only take place ten times per second and will have a frequency of 10 Hz, which is exactly equal to the difference of the frequencies of the two oscillations involved.

Component sounds	Sum of the components	Decomposition into beat and perceived frequencies

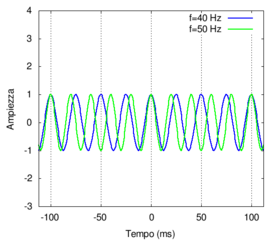
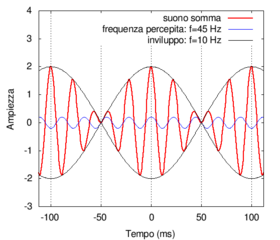
Beats in music

• Perhaps you have seen a guitarist try to tune their guitar by repeatedly and alternately plucking two nearby strings while tightening or loosening them until they hear that the two obtained sounds are in unison;
• or perhaps you have had the fortune to hear the wonderful effect of a Gregorian chorus in a gothic cathedral or an organ being played in the vox humana register. The sound seems to slowly "pulse" with a slow altering of intensity over time;
• or perhaps you have heard a toy (or out of tune) piano produce harsh and dissonant sounds that are similar to those emitted by a "modem" when it is searching for a connection. All of these phenomena are examples of beats.

All of these are manifestations of beats in music.

The beat phenomenon is primarily evident in the superposition of pure sounds (which are sinusoidal waves) and the complete disappearance of sound at regular intervals is obtained only when two sounds have the same intensity. These ideal conditions are difficult to obtain with real sounds, especially when they are produced by two different instruments. However, beats manifest in music much more frequently than is believed, although a trained ear is often needed to recognise them.

In some cases, we can artificially reproduce the necessary conditions; e.g. exploiting the sound produced by two tuning forks (small metallic prongs designed to generate particularly pure sounds). It is a common experience to observe that when tuning forks are perfectly tuned, you can produce the beat phenomenon by slightly modifying the frequency of one of the two forks. This can be obtained by applying a small mass to one of the two tines and thereby modifying the eigenfrequency of oscillation. The sound can also be seen using a microphone and an oscilloscope to visualise the obtained sound. The delicate aspect of the experiment lies in producing sounds of the same pitch in the percussion of tuning forks.

In some rare cases of real listening, the ideal conditions create "themselves":

• when an organ is not perfectly tuned, beats will be frequently heard when a register activates two different rows of pipes. Moreover, as we said at the top of this page, there are registers with specifically tuned beat frequencies to produce the phenomenon of "tremolo" (the vox humana register).
• two facing organs (a layout that occurs in some churches) can also give rise to this phenomenon in its pure form, when soft registers (registers in which the fundamental is the dominant component of the sound) are played.
• on a string instrument, when the same note is played simultaneously on two different strings: if one note is kept fixed while the other is slightly out of tune adjustable beats can be obtained. On unfretted instruments, such as the violin or the cello, this effect can be obtained by playing one open string and fingering the other in such a way as to play a note having almost the same pitch as the first one.

Beats are more often “hidden” and occur between harmonic components of complex sounds.

This topic is delicate and discussed on several pages of this website (see the links at the bottom of this page). Briefly, we can observe that when we superimpose two complex sounds (i.e. composed of the sum of many pure sounds), even if the fundamentals of the two sounds do not have very close frequencies, it is possible that some upper harmonics will generate beats. Even if the beat is not clearly perceptible as such, the two sounds are less pleasant with respect to the case in which the harmonics do not beat. Perhaps this is the definition of "dissonance"?

In this "hidden" form, beats are usually used by tuners and musicians to tune instruments.

Beats and tuning

• We have already observed how beats between the fundamentals of two guitar strings can be used to tune the instrument.
• In the case of unfretted instruments (such as the violin), it is also possible to obtain a particular form of beats, perceived as a ghost sound, called Tartini's third sound.
• From this point of view, the piano is a more complex and interesting instrument. In fact, on the piano, two or three identical strings are struck simultaneously by a hammer to produce a single note and they must generate the least possible number of beats in order to give perfect unison to the note. However, the three strings struck by pressure on an individual piano key are not independent oscillators; they are coupled through the soundboard and by physics (coupled oscillators). We know that every time two oscillators are coupled, the eigenfrequencies of a system change and, in particular, vibration modes are possible in which the energy passes from one oscillator to the other periodically. These modes are responsible for acoustic beats.

Briefly, beats appear in various situations on the piano:

1. When the three strings of a key are not perfectly tuned (resulting in undesirable beats of the fundamental).
2. To a lesser extent, when the three strings of a key are perfectly tuned (resulting in desirable slow beats that add warmth to the sound).
3. When two different keys are struck, beats always appear in the upper harmonics (this is imperceptible to the untrained ear but used by tuners to correctly tune piano keys).

In other instruments, beats are always part of the timbre. In particular, in percussion instruments; both those with defined pitch, such as the timpani, and those with undefined pitch, such as the snare drum or triangle]. In fact, percussion instruments are characterised by the fact that their harmonics are not in whole ratios and, therefore, various "internal" beats (in different harmonics produced by the same sounds) are always present.

Sometimes, there is only one highly evident beat (for an example, see this sample sound of a timpani. Other times, there are so many of them that they give the sound a changing and fluctuating aspect (as in the case of the triangle).

An untrained ear perceives the beats of the upper harmonics, without being able to distinguish them, as a "wobbling" or "harsh" sound or simply as an "out of tuned interval" or as a "not flat", "warm" or "modulated" sound (which is the aspect the musicians seek).

Links

Beats are studied in the fields of acoustic physics, physiology of perception and music theory, as well the topic appears throughout this website. In particular, on the following pages:

• Physiology of the auditory system (with particular reference to von Helmholtz "positional theory").
• Sound or noise?
• Perception of timbre
• How is a musical scale built?
• Almost all the pages on individual musical instruments contain acoustic samples of beats analysed in detail; in particular, see the pages on the piano, timpani and triangle.

Links

• If you visit our 2D Wave virtual laboratory, you will find a prepared experiment where you fully experience this double oscillation dynamically. In our Fourier applet, you will find a sound sample in which you can modify the individual sound components.
• A particular form of beats called modulation is used in some types of radio transmissions.

---

---