Interferenza di onde armoniche

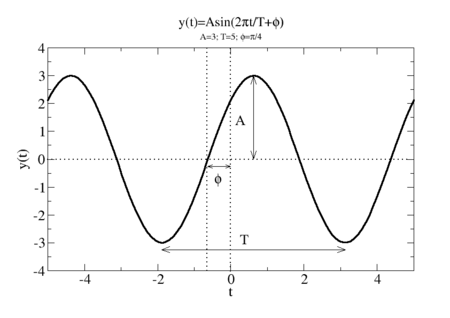
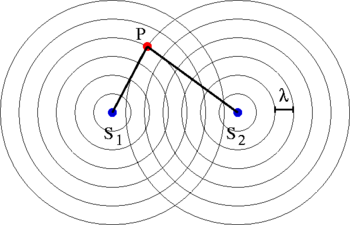
Immaginiamo di avere due sorgenti puntiformi ${\displaystyle S_{1}}$ e ${\displaystyle S_{2}}$che emettano onde periodiche della stessa ampiezza, frequenza e fase.

Immaginiamo inoltre che il moto oscillatorio delle due sorgenti puntiformi ${\displaystyle S_{1}}$ e ${\displaystyle S_{2}}$ sia "armonico" cioè espresso da una funzione matematica del tipo

${\displaystyle y_{S_{1}}(t)=y_{S_{2}}(t)=A\sin(\omega t+\phi )}$

(per una rapida introduzione alle funzioni trigonometriche si veda la pagina le funzioni seno e coseno)

simbolo significato ${\displaystyle A\!}$ ampiezza della sinusoide ${\displaystyle \omega \!}$ frequenza angolare. Essa è legata al periodo T dall'espressione ${\displaystyle \omega ={\frac {2\pi }{T}}}$ ${\displaystyle \phi \!}$ fase dell'onda. Essa specifica la posizione iniziale della sorgente all'istante t=0. Si ha infatti ${\displaystyle y_{S}(0)=A\sin(\phi )\!}$

Tali onde si propagano nello spazio circostante le sorgenti e, quando arrivano nel medesimo punto P, si sovrappongono interferendo. Ci chiediamo sotto quali condizioni il punto P è un punto di interferenza (totalmente) costruttiva. E' facile comprendere che ciò accade quando due "massimi", per così dire, arrivano nel punto P nel medesimo istante. Le condizioni di interferenza costruttiva e distruttiva in un generico punto P ottenute per onde periodiche generiche, già espresse in termini di differenze di tempi e di lunghezze nella pagina aspetti matematici dell'interferenza, possono essere ora ricavate sfruttando le peculiari proprietà matematiche delle funzioni seno che si sovrappongono nel punto P. Detti ${\displaystyle t_{1}}$ e ${\displaystyle t_{2}}$ i tempi necessari all'onda per percorrere lo spazio che separa P da ${\displaystyle S_{1}}$ e ${\displaystyle S_{2}}$, vediamo che nel punto P viene riprodotto il moto delle sorgenti con un certo tempo di ritardo dato proprio da ${\displaystyle t_{1}}$ e ${\displaystyle t_{2}}$ (si veda la sezione come si descrive un'onda?).

La funzione d'onda totale nel punto P è quindi data da

${\displaystyle y(\mathbf {P} ,t)=y_{S_{1}}(t-t_{1})+y_{S_{2}}(t-t_{2})}$

${\displaystyle =A\sin[\omega (t-t_{1})+\phi ]+A\sin[\omega (t-t_{2})+\phi ]\!}$

${\displaystyle =A\sin \theta _{1}(t)+A\sin \theta _{2}(t)\!}$

ove si è posto

${\displaystyle \theta _{1}(t)=\omega (t-t_{1})+\phi \!}$

${\displaystyle \theta _{2}(t)=\omega (t-t_{2})+\phi \!}$

Interferenza costruttiva di onde armoniche in fase

La condizione di interferenza costruttiva si ottiene imponendo semplicemente che la differenza (in modulo) degli argomenti ${\displaystyle \theta _{1}(t)}$ e ${\displaystyle \theta _{2}(t)}$ sia un multiplo di ${\displaystyle 2\pi }$. Si ottiene allora

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\omega \left|t_{1}-t_{2}\right|=2k\pi }$ con ${\displaystyle k=0,1,2,\ldots }$ (1)

Dalla (1) si deduce che la condizione di interferenza costruttiva è indipendente dal tempo t ma dipende solo dalle posizione del punto P (univocamente determinata dai tempi di ritardo ${\displaystyle t_{1}}$ e ${\displaystyle t_{2}}$. Inoltre essendo ${\displaystyle \omega ={\frac {2\pi }{T}}}$ la (1) si trasforma

${\displaystyle \omega \left|t_{1}-t_{2}\right|={\frac {2\pi }{T}}\left|t_{1}-t_{2}\right|=2k\pi }$

da cui

${\displaystyle \left|t_{1}-t_{2}\right|=k\cdot T}$ con

${\displaystyle k=0,1,2,\ldots }$

(1*)

che ricalca la condizione in termini di tempo già ricavata nelle condizioni generali di interferenza.

Interferenza distruttiva di onde armoniche in fase

La condizione di interferenza distruttiva si ottiene imponendo semplicemente che la differenza (in modulo) degli argomenti ${\displaystyle \theta _{1}(t)}$ e ${\displaystyle \theta _{2}(t)}$ sia un multiplo dispari di ${\displaystyle \pi }$. Si ottiene allora

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\omega \left|t_{1}-t_{2}\right|=(2k+1)\pi }$ con

${\displaystyle k=0,1,2,\ldots }$

(2)

Dalla (2) si deduce che la condizione di interferenza distruttiva è indipendente dal tempo t ma dipende solo dalle posizione del punto P (univocamente determinata dai tempi di ritardo ${\displaystyle t_{1}}$ e ${\displaystyle t_{2}}$. Inoltre essendo ${\displaystyle \omega ={\frac {2\pi }{T}}}$ la (1) si trasforma

${\displaystyle \omega \left|t_{1}-t_{2}\right|={\frac {2\pi }{T}}\left|t_{1}-t_{2}\right|=(2k+1)\pi }$

da cui

${\displaystyle \left|t_{1}-t_{2}\right|=(2k+1)\cdot T}$ con ${\displaystyle k=0,1,2,\ldots }$, (2*)

che ricalca la condizione in termini di tempo già ricavata nelle condizioni generali di interferenza.

Interferenza di onde armoniche sfasate

Immaginiamo che le due sorgenti puntiformi ${\displaystyle S_{1}}$ e ${\displaystyle S_{2}}$ che emettano onde armoniche della stessa ampiezza, frequenza ma in modo non sincronizzato. Si assuma ad esempio che la sorgente ${\displaystyle S_{2}}$ riproduca l'oscillazione della sorgente ${\displaystyle S_{1}}$ con un certo tempo di sfasamento che indicheremo con ${\displaystyle t_{s}}$. Assumeremo

${\displaystyle t_{s}>0\!}$ se la sorgente ${\displaystyle S_{2}}$ oscilla in ritardo rispetto a ${\displaystyle S_{1}}$

${\displaystyle t_{s}<0\!}$ se la sorgente ${\displaystyle S_{2}}$ oscilla in anticipo rispetto a ${\displaystyle S_{1}}$

Se il moto della sorgente ${\displaystyle S_{1}}$ è descritto dalla funzione

${\displaystyle y_{S_{1}}(t)=A\sin(\omega t+\phi )}$,

allora il moto della sorgente ${\displaystyle S_{2}}$ è descritto da

${\displaystyle y_{S_{2}}(t)=y_{S_{1}}(t-t_{s})=A\sin(\omega (t-t_{s})+\phi )}$.

Se poi il tempo di sfasamento ${\displaystyle t_{s}}$ è una frazione nota del periodo T, cioè

${\displaystyle t_{s}=\pm \alpha T}$ con ${\displaystyle \alpha \in \left]0;1\right[}$

ricordando, al solito, che ${\displaystyle \omega ={\frac {2\pi }{T}}}$ si ottiene

${\displaystyle y_{S_{2}}(t)=A\sin[\omega (t\mp \alpha T)+\phi ]=A\sin(\omega t+\phi \mp 2\pi \alpha )}$.

In pratica lo sfasamento introduce un angolo di fase ${\displaystyle 2\pi \alpha }$ che permette di riformulare immediatamente le condizioni di interferenza costruttiva (1) e distruttiva (2).

Ponendo

${\displaystyle \theta _{1}(t)=\omega (t-t_{1})+\phi \!}$

${\displaystyle \theta _{2}(t)=\omega (t-t_{2})+\phi \mp 2\pi \alpha \!}$

la condizione (1) diventa

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\left|\omega (t_{1}-t_{2})\pm 2\pi \alpha \right|=2k\pi }$ con

${\displaystyle k=0,1,2,\ldots }$

(1**)

e la condizione (2) diventa

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\left|\omega (t_{1}-t_{2})\pm 2\pi \alpha \right|=(2k+1)\pi }$ con

${\displaystyle k=0,1,2,\ldots }$

(2**)

Interferenza tra sorgenti non isofrequenziali

Tutte le condizioni di interferenza precedenti sono state dedotte nell'ipotesi che le due sorgenti interferenti fossero isofrequenziali. Le condizioni che ne sono risultate sono indipendenti dal tempo ma dipendono solo dalla posizione del punto P nello spazio.

Se le sorgenti non oscillano alla stessa frequenza si hanno condizioni di interferenza, in un dato punto dello spazio, che evolvono nel tempo rendendo lo studio del fenomeno estremamente complesso. Supponiamo di avere di sorgenti "armoniche" ${\displaystyle S_{1}}$ e ${\displaystyle S_{2}}$ (aventi stessa ampiezza e fase) di frequenza differente. Il moto oscillatorio delle due sorgente può, al solito, essere espresso da

${\displaystyle y_{S_{1}}(t)=A\sin(\omega _{1}t+\phi )}$,

${\displaystyle y_{S_{2}}(t)=A\sin(\omega _{2}t+\phi )}$,

con :${\displaystyle \omega _{1}\neq \omega _{2}}$; ripetendo la derivazione fatta, ad esempio nel caso interferenza costruttiva, la condizione (1) diventa ora

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\left|(\omega _{1}-\omega _{2})t+\omega _{1}t_{1}-\omega _{2}t_{2}\right|=2k\pi }$ con

${\displaystyle k=0,1,2,\ldots }$

(1***)

che, come si vede, dipende dal tempo t.

Battimenti

Se le due sorgenti non isofrequenziali sono collocate nello stesso punto dello spazio è chiaro che, fissato un punto P, i tempi di ritardo ${\displaystyle t_{1}}$ e ${\displaystyle t_{2}}$ vengono a coincidere. Se poniamo ${\displaystyle t_{1}=t_{2}={\frac {x}{v}}}$, la condizione di interferenza (1***) rimane tempo-dipendente ma assume la forma più semplice:

${\displaystyle \left|\theta _{1}(t)-\theta _{2}(t)\right|=\left|(\omega _{1}-\omega _{2})\left(t-{\frac {x}{v}}\right)\right|=2k\pi }$ con

${\displaystyle k=0,1,2,\ldots }$

(1°)

che può scriversi come:

${\displaystyle \left|t-{\frac {x}{v}}\right|={\frac {2k\pi }{\left|(\omega _{1}-\omega _{2})\right|}}=k{\frac {T_{1}\cdot T_{2}}{\left|(T_{1}-T_{2})\right|}}}$ con

${\displaystyle k=0,1,2,\ldots }$

(1°°)

ove., al solito si sono indicati con ${\displaystyle T_{1}}$ e ${\displaystyle T_{2}}$ i periodi delle due sorgenti. Tale condizione fornisce tutti gli istanti di tempo t per cui, nel punto P, dstante x dalle due sorgenti, vi è interferenza costruttiva. Se consideriamo due istanti consecutivi (assunti cioè per valori k e k+1) e valutiamo la loro differenza ${\displaystyle \Delta t}$

${\displaystyle \Delta t={\frac {\left|(T_{1}-T_{2})\right|}{T_{1}\cdot T_{2}}}}$

ci accorgiamo che, fissato un punto dello spazio, la condizione di interferenza si ripresenta ogni ${\displaystyle {\frac {T_{1}\cdot T_{2}}{\left|(T_{1}-T_{2})\right|}}}$ secondi, ha cioè un andamento periodico di frequenza

${\displaystyle f={\frac {1}{\Delta t}}={\frac {\left|(T_{1}-T_{2})\right|}{T_{1}\cdot T_{2}}}=\left|f_{1}-f_{2}\right|}$

ove, nell'ultimo passaggio, si è usata la relazione generale tra periodo e frequenza ponendo ${\displaystyle f_{1}={\frac {1}{T_{1}}}}$ e ${\displaystyle f_{2}={\frac {1}{T_{2}}}}$.

La frequenza ${\displaystyle f=\left|f_{1}-f_{2}\right|}$ viene detta frequenza di battimento. Prendendo ${\displaystyle f_{1}}$ e ${\displaystyle f_{2}}$ quasi uguali la frequenza di battimento può essere resa molto minore delle singole frequenze delle due sorgenti interferenti.

Un'ultima osservazione: tutto il ragionamento è stato svolto partendo dalla condizione di interferenza costruttiva. Esso rimane comunque valido anche partendo dalla condizione (2) di interferenza distruttiva.

Laboratorio virtuale: esperimenti di interferenza

Se sei interessato a visualizzare fenomeni di interferenza collegati al nostro laboratorio virtuale Onde 2D. Ti proponiamo di seguito una serie di esperienze guidate, ma puoi benissimo sperimentare nuove configurazioni e nuovi esperimenti. L'applet è molto intuitivo; per una corretta comprensione di quello che osservi, tieni solo presente che le zone colorate rappresentano l'ampiezza dell'oscillazione. Tanto più brillante appare il colore, maggiore è l'ampiezza delle oscillazioni (verde per le cime, rosso per le valli). Ovviamente le zone di buio rappresentano assenza di oscillazione causata dall'interferenza distruttiva.

Esperienze proposte:

• Interferenza tra due o più sorgenti puntiformi isofrequenziali
• Interferenza tra due sorgenti puntiformi non isofrequenziali
• Interferenza tra onde di frequenze diverse generate da un'unica sorgente (battimenti)

---