Vibrations, supersonic bangs and sources of impulsive noise

In this video, various sources of both impulsive noise and noise generated by vibration and resonance are illustrated through comments on high-speed videos. These allow us to see phenomena that our eyes cannot resolve but that our ears can. See the page on Sound and resonance as well.

© 2006 The University of Salford with the kind permission of the author, Prof. Trevor J. Cox, https://hub.salford.ac.uk/sirc-acoustics. Translation and subtitles by Carlo A. Rozzi.

Sound or noise?

In the following paragraphs, we have created several acoustic examples to put the traditional distinction between sound and noise to the test.

Three easy "pieces"

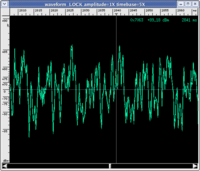
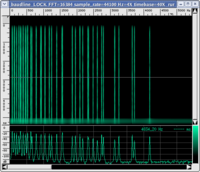
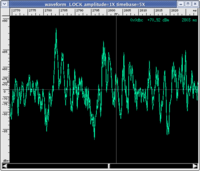
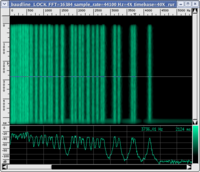
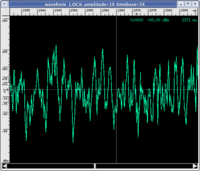
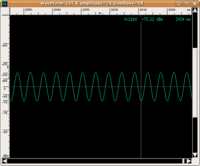
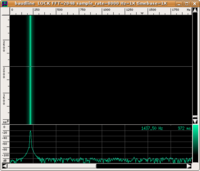
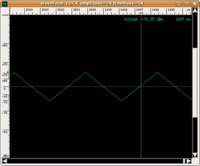
Many elementary surveys on this topic affirm that what seems to characterise sound with respect to noise is its description in terms of a periodic wave. The spectrogram must contain only pure multiple frequency sounds of a fundamental frequency. The following are graphic illustrations of waves that are periodic and non-periodic with their respective spectrograms and corresponding sound (click on the images to enlarge them and on the audio files to listen to them. If you want more information on how to read a spectrogram, visit this page with instructions)

Graph	Spectrogram	Audio
		puro_220_Hz.wav Pure (sinusoid) sound at 220 Hz.
		triangolo_220_Hz.wav Triangular wave with fundamental at 220 Hz.
		rumore_bianco.wav White noise (uniform spectrum).

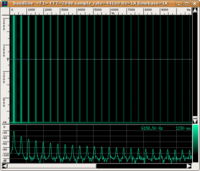
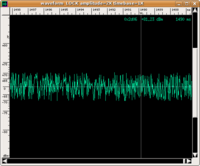
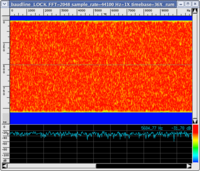
Let us first observe that not all sounds associated with a periodic wave are "pleasant" (many listeners find sinusoid and triangular waves irritating and, certainly, beyond any subjective judgement of pleasantness, they are "objectively" uninteresting. However, if we limit ourselves to these examples, it seems to confirm the most elementary association: a well-defined pitch can be associated with a periodic wave, while it cannot be attributed to white noise. For example, it does not make sense to ask ourselves if it is more or less acute than the sinusoid. To put the definition to the test, we should consider a few, more complex examples.

Less easy "Pieces"

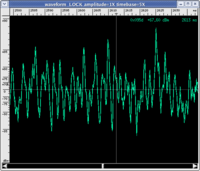
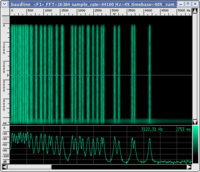
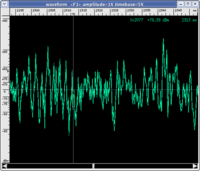
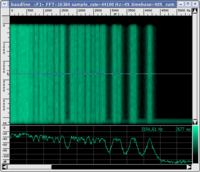
This question is a bit more complex. Wave periodicity is not a sufficient condition to call what we hear sound, even if we neglect the aesthetic judgement of the sounds produced by periodic signals. In fact we cannot say that periodic waves necessarily generate sounds within the range of audible frequencies. Listen to the AUDIO example below.

Graph	Spectrogram	Audio
		battimenti_220_245_Hz.mp3 Overlapping of two pure sounds at 220 and 245 Hz

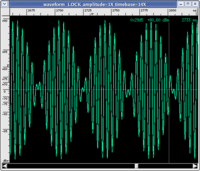
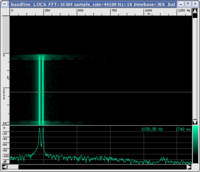
Even with the presence of a periodic wave (the graph leaves no doubt), it would be difficult to call what you just heard sound. You just listened to what is called in acoustics a beat. In this case, the sensation of noise (even with the presence of periodic waves) is due to a perceptual mechanism: our auditory system is "confused" when it is hit by sounds of very close frequencies and is unable to discriminate their pitch, it perceives a sound with an intermediate pitch but of a "rough" nature, therefore, noisy. This is how the two components sound when heard individually (if you wish to study this topic further, visit the page on critical bands and beats).

puro_220_Hz.mp3 Pure sound at 220 Hz

puro_245_Hz.mp3 Pure sound at 245 Hz

"Harmonic noise"

It is easy to realise that (exact) periodicity is not a necessary condition to distinguish sound from noise. For two reasons:

• the auditory system seems to tolerate small deviations from periodicity (if you wish to study this topic further, visit the page on perception of pitch);
• no sound has a wave form that is exactly periodic. A funzione periodica_en|periodic function has always been and will always be a given thing, while sound is something that is born, evolves over time and dies. After all, think of how boring a sound that was constantly the same would be!
• Certainly, if there is no periodicity, not even remotely, in a sound phenomenon, it is merely noise. In this case, a sound wave has contenuto spettrale_en|spectral content made up of sounds of any frequency and pitch.

In fact, it is possible to produce examples of non-periodic waves that our ear considers to be a pleasant and consonant sound such as:

Graph	Spectrogram	Audio
		rumore_armonico_2.wav Harmonic noise. Bands include Do2 Do3 Mi♭4 So4 Ti♭4 Do5. The width of each band is 2 Hz.
		rumore_armonico_10.wav Harmonic noise. Bands include Do2 Do3 Mi♭4 So4 Ti♭4 Do5. The width of each band is 10 Hz.
		rumore_armonico_20.wav Harmonic noise. Bands include Do2 Do3 Mi♭4 So4 Ti♭4 Do5. The width of each band is 20 Hz.
		rumore_armonico_40.wav Harmonic noise. Bands include Do2 Do3 Mi♭4 So4 Ti♭4 Do5. The width of each band is 40 Hz.
		rumore_armonico_100.wav Harmonic noise. Bands include Do2 Do3 Mi♭4 So4 Ti♭4 Do5. The width of each band is 100 Hz.

Harmonic noise is obtained by overlapping various bands of white noise, each of which is centred on an integer multiple of the chosen fundamental frequency. When the bands are ideally very narrow, the spectrum becomes identical to that of a pleasant sound, while the wider the individual bands are, the more the character of noise takes over. In all cases, the resulting sound wave possesses periodic components but, in the strictest sense, it is never exactly periodic because a random component is always present, except in the limit of infinitely narrow bands.

Harmonic noise seems to reveal a fundamental characteristic of perception that conveys information by the degree of consonance or pleasantness of a sound wave. This information is of inestimable value to musicians. For more on this topic, see the pages on harmony and harmonic sounds and consonance and dissonance).

---