Percezione del timbro en
Da "Fisica, onde Musica": un sito web su fisica delle onde e del suono, acustica degli strumenti musicali, scale musicali, armonia e musica.
Jump to navigation Jump to searchWhat is the timbre of a sound
A commonly accepted definition of timbre is the following:
- timbre is the quality of a perceived sound that allows us to distinguish two different sounds that have the same pitch and loudness.
In other words, timbre is the quality of sound that allows us to distinguish the voice of a violin from that of a flute, when the two instruments are emitting the same note. Listen to these examples in which a violin, flute and trumpet are emitting a B flat of the central octave of the piano (about 466 Hz).
| Instrument | Wave shape | Spectrogram | Audio | |
|---|---|---|---|---|
| Violin |
|
|
|
|
| Flute |
|
|

|
|
| Trumpet |
|
|
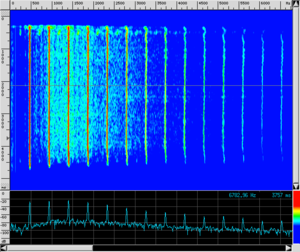
|
|
| Oboe |
|
|
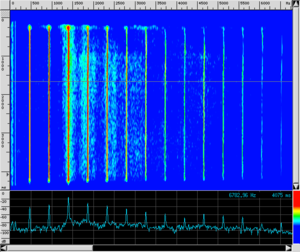
|
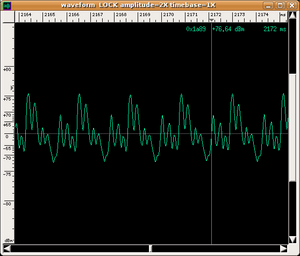
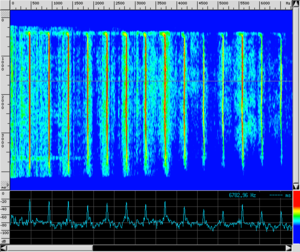
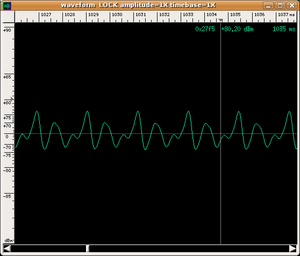
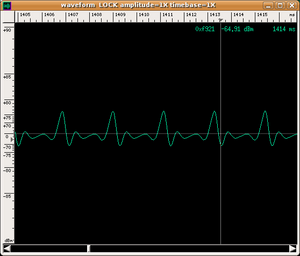
There is no doubt that the musicians are emitting notes with the same pitch and even a non-musically trained ear can perceive the different sound qualities of these notes. To assist the eye, we have also presented both the wave shape recorded as a function of time and the spectrogram (see How is a spectrogram read? for a guide on how to read it).
What factors determine perceived timbre?
A "static" answer
The answer to this question becomes extremely intricate if we try to define timbre not on the basis of what it permits us to do (distinguish different musical instruments) but on the basis of objective and measurable parameters.
- A common answer in literature is that the timbre of an instrument is largely due to the spectral composition of the sound that it emits. The concept of spectral content is complex (you will find it well illustrated on the page about Fourier's theorem). To simplify it, we can say that when an instrument emits a note of a given frequency (e.g. the B flat heard previously), due to the boundary conditions imposed by the "geometry" of the oscillating parts of the instrument, along with the fundamental note, it generates more notes at integer multiple frequencies of the fundamental (called harmonics).
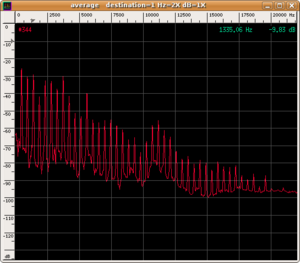
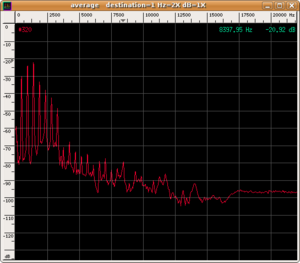
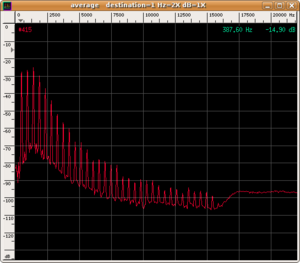
The spectrum of various instruments differs due to the different distributions of energy (and, therefore, of amplitudes) between the fundamental note and the upper harmonics. In fact, comparing the spectra of the three preceding sounds, we can observe the different contributions of the various harmonics
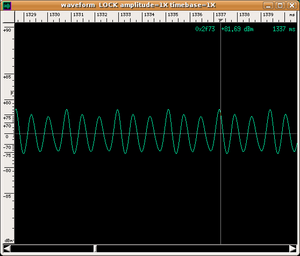
- To each spectrum there corresponds a very precise wave shape obtained by "adding" the various harmonics. This process is called sound synthesis; therefore, we can say in short that the timbre of an instrument is largely due to the wave shape of the sound that it emits. The following are the wave shapes of our three sounds:
The difference in the three wave shapes is evident.
- In our virtual lab, you can find an applet with which you can have fun synthesizing new sounds and deciding which harmonics to include and with what weight (i.e. by regulating their amplitude). The applet allows you to see the action of superposition of various harmonics on the wave shape in real time. In principle, you can try to faithfully reproduce the wave shapes of the three preceding real sounds acting on the frequency of the fundamental note and on the amplitude of the following harmonics. The result will be disappointing: while this wave shape will resemble the real one, the timbre obtained is far from similar to that of a real instrument. We wish to specify that this disappointing result is not the result of approximations made by the "software" but the consequences of an attempt to define the timbre of an instrument in static terms.
A dynamic answer
As a matter of fact, sound is a "living" entity that follows a well-defined sequence of various time phases: generally
- an attack,
- a sustain phase
- a release phase.
- During these phases, the spectral content of emitted sound varies over time.
The spectra shown in the preceding paragraph, which "photograph" the average spectral content over time for the duration of the sound, are completely unable to explain the complex perception of timbre. It would be like wanting to understand an entire film by seeing only one frame. "Static" spectra give a decent approximation of real timbre only for the sustain phase of such instruments as strings or winds, for which it is possible to make the sound "last". Even if the attack and decay phases always contribute to the determination of timbre, sounds produced by these kinds of instruments can remain stationary and prolonged at will. However, for percussion instruments, once sounds are generated, they are no longer under the control of the player. Their timbre can never be synthesized from a static spectrum. It is for this reason that the applet only presents attempts to reproduce the timbre of a few instruments (e.g. oboe, clarinet and violin).
|
- Remember that real sounds (you will find many examples on the pages about musical instruments) contain anharmonic partials (not multiples of the fundamental) generated by the mechanical "noises" of the moving parts of instruments. In fact, many people say that it is these very tiny noises that make the sounds produced by an instrument less cold than synthesized sounds.
From these considerations emerges a much more complex answer to our initial question, even though we will see that it is still not satisfactory: the timbre of an instrument is determined by the evolution of its spectral content of sound over time. As a matter of fact, in the timbre analysis of sounds, sonograms are of fundamental importance. They are none other than the representation of the time evolution of the sound spectrum (like a film composed of many frames).
Concept of the envelope
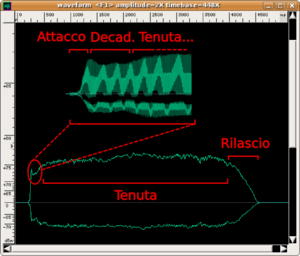
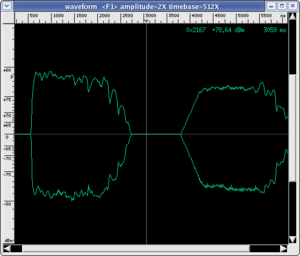
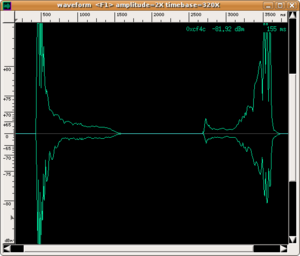
The use of sonograms to capture the time evolution of timbre is often accompanied by an analysis of the envelope of the sound produced. With this term, we mean the evolution of the amplitude of the sound wave over time (NB: instead of the term amplitude, musicians use the term dynamics). In the envelope of a sound, four phases can always be distinguished (but not all are always present).
- Attack: which is the initial phase of sound that lasts until the moment when the sound wave reaches its maximum amplitude. It can be very quick, as with percussion instruments and the piano (duration of about 1/100 of a second), or spread out over time. For string and wind instruments, the player can vary the type of attack by modulating its duration and the way of reaching the energy peak according to their musical needs. Obviously, every sound has an attack phase because every physical vibrating system responds with a characteristic time; which is the time necessary for stationary waves to form or for a particular normal mode of vibration of the system to emerge. Listen to the musical examples below, which were executed by real musicians in a recording studio specifically for us.
- Decay: which is also called initial decay or first decay. It is present in those instruments (e.g. trumpet) in which sound appears only if some physical parameter (e.g. breath pressure) rises above a given threshold. In these cases, the musician slightly corrects the "discontinuity" created by reaching the threshold, which causes a brief diminution of amplitude before the stabilisation phase of the sound.
- Sustain: is the phase in which a sound remains stable while the player continues to supply energy. Obviously, this phase does not exist for percussion instruments. It is interesting to observe that this phase seems to be the easiest to reproduce with an electronic synthesizer. In this phase, the player actually introduces involuntary fluctuations of amplitude, which characterise the sound of "real" instruments with respect to electronic ones.
- Release: which is also called final decay. This phase begins at the moment in which the player stops supplying energy to the instrument and the sound decays more or less rapidly. This phase can also be very long for percussive instruments (think of the base note of a piano as oppose to the sound of a gong), while it is usually short in wind and strings. Obviously, all sounds have a release.
| envelopes of the wave shape | |||||
|---|---|---|---|---|---|
| violin | flute | trumpet | |||
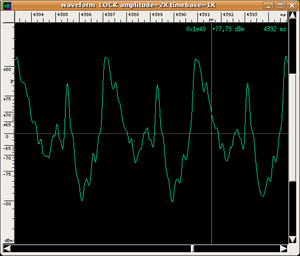
|
|
|
|||
|
|
|
|||
Modern electronic synthesizers have a "circuitry" that blends both these four phases and their spectral content according to parameters that are easily regulated by the player. The control of timbre reached in these instruments no longer aims to recreate the sound of traditional instruments. "Electronic" sound now has an autonomous existence (music is now composed specifically for synthesizers), which is constantly enriched by the (theoretically unlimited) possibility of constructing wave shapes that cannot be generated by traditional instruments.
Theory of the formants
If we think about it carefully, the answer given in the preceding paragraph, although more focused on the dynamic aspects related to the timbre of sound, is still unsatisfactory for that which regards perceptual aspects. This happens for several reasons:
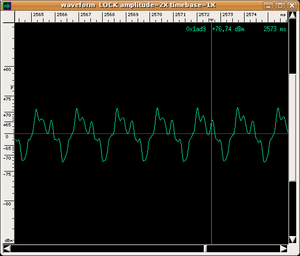
- sonograms of sounds of different pitch generated by the same instrument have a different time evolution; i.e. they are not obtained by simply "shifting" the frequencies. This is due to the different time evolution of the various harmonics making up sounds (so, in theory, for each instrument we should identify a set of different timbres, one per note);
| wave shape | ||
|---|---|---|
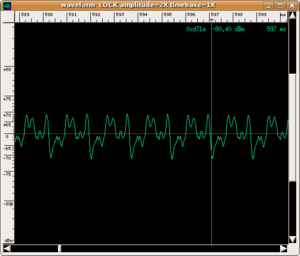
|
|
|
| sonogram | audio | |
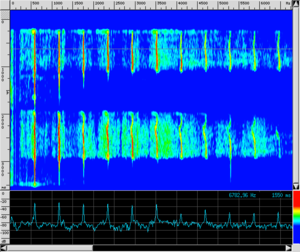
|
|
|
- also, the same note played in two different ways (e.g. an A played on the 2nd open string or on the 3rd fingered string of a violin) has slightly different (even instantaneous) sound spectra (and this would increase the number of timbres to be associated with the instrument);
| wave shape | ||
|---|---|---|
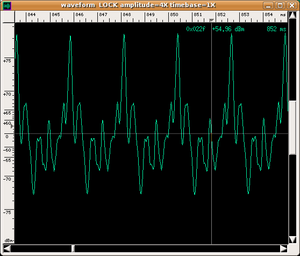
|
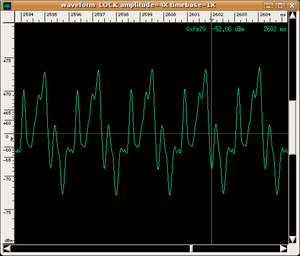
|
|
| sonogram | audio | |
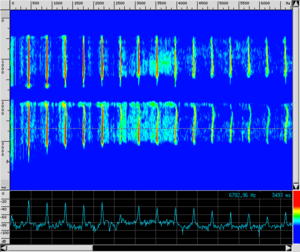
|
|
|
- in many experiments, we can within certain limits, modify the sonogram of a pure sound and yet still recognise the timbre of the instrument that produces it. For example, it is easy for us to recognise instruments when we hear them on the radio, even though the radio acts as a filter and attenuates a large number of the original frequencies. Somehow, our perceptual apparatus can recognise not only a wide set of sonograms but also a great number of their modifications!
Evidently, there is something else that allow us to recognise an instrument besides the evolution of its spectral content of sound over time. This is what the formants theory suggests. To fully understand this theory, we encourage you to read the pages on sound and resonance and musical instruments. In any case, let us summarise the fundamental assumptions of the theory.
From a physicist's point of view, a musical instrument is simply a system that generates sound waves and radiates them in the environment. It is composed of (at least):
-
- a primary source of vibration (string, membrane, plate, air) tuneable to various frequencies that generates a fundamental and a number partials (harmonic or not) with an amplitude that decreases at higher frequencies;
- a resonator (body, closed or open bore, sound board) that amplifies the vibration at certain frequencies and gives a new shape to the sound waves with respect to those originally emitted by the vibrating element;
- an impedance adapter between the vibrating system and the surrounding air that increases the efficiency of sound radiation.
The most interesting thing for us is the selective amplification performed by the resonator. The specific shape of each musical instrument has been designed so that its resonator has precise resonance frequencies. For example, the resonator of the violin is its body, the irregular shape of which selects resonating frequencies from about 600 Hz to 1000 Hz (called wood resonance) and other very close resonances from 2000 Hz to 4000 Hz. An air resonance also exists and is called Helmholtz resonance due to the air that enters and exits the body through the f-shaped holes at a frequency of around 300 Hz. When this resonator is struck by a vibration generated by the vibrating element (the coupling between the vibrating element and resonator is enhanced by adapting the impedance between the body and string through the bridge), it "resonates"; i.e. it starts oscillating at frequencies near its resonance frequency and independently of the sound spectrum of the primary source of vibration. The practical effect is that the spectral content of the original sound is modified by the filtering effect of the resonator. Frequency bands called formants are formed, in which the sound emission of the instrument is dominant. Probably, the position of the formants, due to the geometry of the instrument and not the frequency of the radiated note, is the determining element for the recognisability of the timbre of the instrument. A practical method for obtaining the frequencies of the formants corresponding to the resonances of an instrument is to average the instantaneous spectrograms over sufficiently long time intervals. It is important to calculate the average over long times and on pieces that span the entire range of the instrument in order to excite all the normal modes of the body.
... And the poor player?
As said earlier, it seems that the timbre quality of an instrument is completely dependent on the geometric characteristics of the instrument itself. From a physics point of view, the role of the player is reduced to being the:
- source of mechanical energy to excite the primary source of vibration;
- selector of the fundamental harmonic (i.e. of the emitted note) modifying the physical characteristics (e.g. string length) of the vibrating element. In many instruments (e.g. the piano), the pitch of the played note is already regulated by its corresponding key; therefore, the musician appears to be even more useless!
So, real life musicians are actually not needed! We are well aware of the fact that when musicians generate a sound for a given note (i.e. given the frequency of the fundamental harmonic), they can control the way and the speed at which energy is distributed in the various harmonics (even by suppressing others). One of the goals of the execution technique (from a very reductionist point of view) is the acquisition of complete control of the timbre of the produced sound. The player of each musical instrument faces specific technical problems stemming from the different ways that the four phases of sound production described previously are performed. Think about the:
- "touch" of the pianist;
- attack of sound by a trumpeter, which can be either quick and produce a characteristic "click" or more spread out over time;
- various ways in which a violinist uses their bow to produce specific timbre changes;
- timbre modulation of the sound of a guitar depending on if it is being played with fingers or a pick;
- timbre modulation of the sound produced by drum cymbals depending on if they are being struck in the centre or near the edge;
- voluntary fluctuations of amplitude and frequency, such as tremolo or vibrato, that the violinist introduces into the sound when executing a sustain phase to make it less flat and boring;
- timbre modulation of singing from the chest (opera singers), from the throat (pop singers), through the nose or in falsetto.
In-depth study and links
- On the pages regarding individual musical instruments (such as the oboe, trumpet, clarinet, violin, timpani, human voice, etc.), you will find live recordings in which you can appreciate the ways that musicians modulate timbre with respect to their instruments.