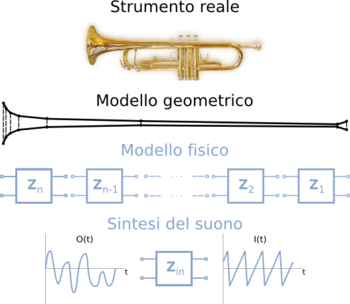
Acustica di strumenti a fiato modello
Da "Fisica, onde Musica": un sito web su fisica delle onde e del suono, acustica degli strumenti musicali, scale musicali, armonia e musica.
Jump to navigation Jump to searchPerché strumenti modello?
Quando in fisica si deve affrontare un problema difficile spesso si adotta la seguente strategia: si risolve prima un problema più semplice.
Lo studio delle proprietà acustiche di uno strumento musicale è quasi sempre un problema piuttosto complesso, e va affrontato con adatti strumenti teorici e sperimentali. Tuttavia, in alcuni casi, considerando elementi particolarmente semplici, è possibile calcolare soluzioni analitiche all'equazione delle onde, ed ottenerne informazioni interessanti. Questi sistemi elementari possono in seguito essere combinati tra loro per ottenere geometrie meno semplici, e costituiscono perciò la base per un'analisi più accurata. Inoltre, proprio perché le soluzioni sono spesso anche concettualmente, oltre che geometricamente semplici, gli strumenti modello permettono al nostro cervello di comprendere davvero la fisica rilevante che governa ciò che accade all'interno e alle estremità del tubo.
Un approccio analogo si adotta anche nell'analisi dei sistemi vibranti, quando si cerca di ridurli ad un insieme di sistemi vibranti semplici (si vedano le pagine su moto armonico, modi normali, risonanza negli edifici). L'oscillatore armonico è il caso di più facile soluzione e comprensione, ma spesso, specie se in combinazione con altri oscillatori, può descrivere accuratamente la vibrazione di strutture assai complesse.
Anche se questi casi semplici non corrispondono esattamente a nessuno strumento dell'orchestra, essi costituiscono un banco di prova ideale per la nostra comprensione dei fenomeni ondulatori. L'equazione delle onde prende una forma facile da risolvere permettendoci di visualizzare la soluzione, e di ricavare e discutere le principali proprietà acustiche. In seguito potremo confrontare le proprietà di questi "strumenti da laboratorio" con quelle degli strumenti veri, per capire fino a che punto il nostro modello sia accurato, e quali ne siano i limiti di applicabilità.
Ipotesi semplificatrici
In una serie di pagine dedicate analizziamo il caso della propagazione delle onde sonore in canne aventi geometrie elementari, tipicamente cilindro, tronco di cono, e combinazioni delle due. La principale ipotesi semplificatrice consiste nell'assumere che la propagazione delle onde avvenga esclusivamente lungo la canna, e non trasversalmente ad essa.
| canna con propagazione: | |
|---|---|
| solo lungo l'asse | anche perpendicolare all'asse |

|

|
Questa ipotesi è fisicamente giustificata almeno finché la sezione della canna rimane non eccessivamente grande. Infatti, considerando le possibili onde stazionarie che si possono instaurare trasversalmente ad una canna con diametro pari ad 1 cm, possiamo facilmente calcolare che la più bassa frequenza ammessa è pari a circa 17 kHz (si veda al proposito Frequenze proprie delle canne). Una frequenza al limite degli ultrasuoni, che quindi non può avere un grande effetto sulla resa acustica della canna. In strumenti di piccolo diametro, quali il flauto, perciò, questa ipotesi è piuttosto realistica. Per una canna avente diametro pari a 5 cm, tuttavia, la frequenza scende a 6 kHz, e l'effetto non può più essere trascurato.
Altri problemi sono posti ad esempio dalla descrizione accurata delle campane che formano la bocca degli ottoni, e che tanto contribuiscono a determinarne la voce caratteristica. Di questi ed altri problemi, quali l'effetto dell'irraggiamento del suono dalle estremità aperte della canna e dell'effetto degli attriti si discuterà meglio nelle singole pagine.
Metodo
Come discusso ampiamente nella pagina dedicata al principio di sovrapposizione e come è evidente scorrendo la tavola dei Livelli di pressione sonora, sappiamo che le onde sonore di interesse per gli strumenti musicali sono onde di pressione corrispondenti ad una leggerissima increspatura rispetto al valore della pressione atmosferica. In altre parole, le onde sonore sono onde di piccola ampiezza, anche per suoni piuttosto forti entro i limiti di tollerabilità dell'orecchio umano. Diversa è la storia nel caso delle onde di shock, come nelle esplosioni, ma queste non ci interessano in questa sede (si veda ad esempio la pagina dedicata ai suoni più intensi). Per questo motivo possiamo sempre trattare la propagazione nella sua approssimazione lineare, ovvero assumere che la risposta di un elemento alla somma di due stimoli altro non sia che la somma delle risposte a ciascuno dei due stimoli. Ciò significa che possiamo adottare il concetto di impedenza per descrivere la risposta delle canne.
Per una discussione approfondita del concetto rimandiamo alle pagine su impedenza, impedenza acustica, adattamento di impedenza, suono e risonanza, e ai loro collegamenti. In questa sede ricordiamo solo che l'impedenza di ingresso di una canna è una proprietà della canna (indipendente quindi dal tipo di stimolo cui è sottoposta) che, per ogni frequenza f, indica il rapporto tra i valori della pressione sonora alla bocca della canna e del flusso d'aria entrante, e il loro reciproco sfasamento
- .
L'unità di misura è l'ohm acustico che corrisponde ad una pressione acustica di una baria su una portata d'aria di 1 cm3 al secondo (si veda impedenza e unità di misura della pressione).
Grazie al principio di sovrapposizione l'impedenza può essere calcolata separatamente per ogni frequenza, eccitando la canna con un segnale sinusoidale puro, mentre la risposta ad un segnale periodico più complesso si otterrà combinando le risposte alle diverse frequenze dello sviluppo del segnale composto (ottenuto applicando il teorema di Fourier). Per vedere alcuni esempi di scomposizioni di segnali complessi in sinusoidi si vedano le pagina teorema di Fourier e sviluppi in serie di Fourier.
L'ampiezza dell'impedenza dei tubi sonori è una grandezza sempre caratterizzata dalla presenza di profondi massimi e minimi, fatto che ci indica chiaramente che i tubi sono dei risuonatori a banda stretta. Essi dunque sono in grado di attenuare tutte le frequenze tranne un piccolo insieme, corrispondente appunto alle frequenze proprie del sistema (si veda anche risonanza, modi normali, frequenze proprie ,frequenze proprie delle canne). Il nostro principale interesse in queste pagine è di capire come siano distribuite queste frequenze di risonanza, in quanto da questo fatto dipendono molte delle caratteristiche del suono emesso dalla canna (si veda percezione del timbro)
Collegamenti
Le pagine sono così organizzate:
- Canna cilindrica: si esaminano le ben note proprietà della canna cilindrica ideale (si veda ad esempio frequenze proprie delle canne) dal punto di vista del concetto di impedenza, e si esamina il caso di canne meno ideali
- Canna cilindrica modificata: si studia l'effetto di un allargamento o una strozzatura sulla risposta della semplice canna cilindrica. Si studia cioè l'effetto dell'accoppiamento delle canne (o guide d'onda) con risuonatori di Helmholtz (o cavità risonanti)
- Canna conica: si confronta la risposta della canna a conica con quella della canna cilindrica, e se ne discute il paradosso
- Canna mista: si combinano elementi cilindrici e tronco-conici in modo semplice per studiare come cambia la risposta.
- rifrazione nelle canne: non riguarda canne assimilabili a quelle che compongono strumenti musicali reali, ma costituisce un'illustrazione alternativa dei concetti di riflessione, rifrazione, adattamento di impedenza,