Frequenze proprie e paragone con la canna cilindrica

La canna tronco-conica (che chiameremo per brevemente solo "conica") è il prototipo di molti strumenti a fiato, quali l'oboe, il fagotto e il saxofono. Le trombe invece hanno canna pressoché cilindrica (eccezion fatta per la campana finale), anche se ne esistono versioni antiche a canna conica. Queste ultime si trovano ancora come parte del canneggio dei maggiori organi da chiesa.

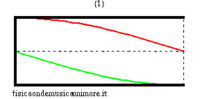
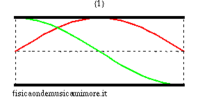
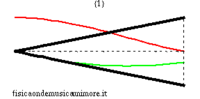
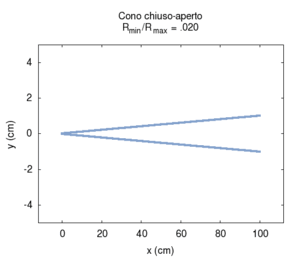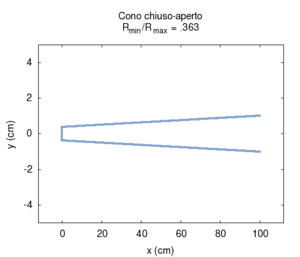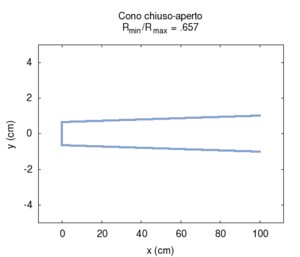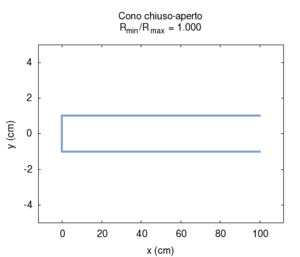
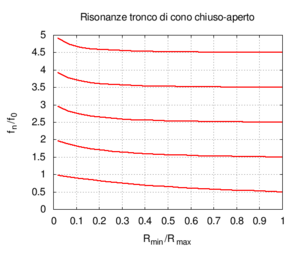
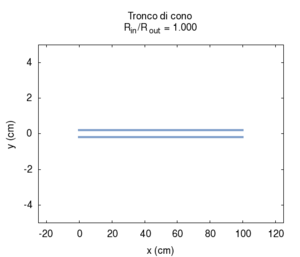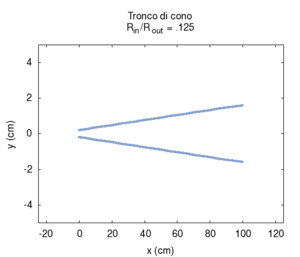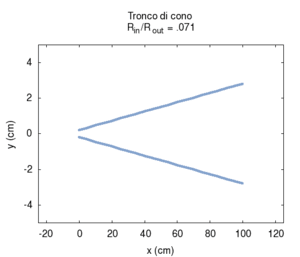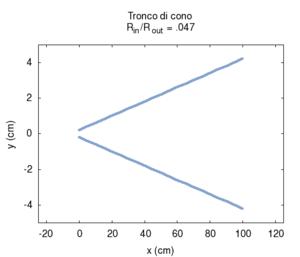
Le proprietà che rendono la canna conica un buon candidato per costruire strumenti musicali sono mostrate nella figura a lato, e sono le stesse che caratterizzano la canna cilindrica:

1. Una canna conica ha frequenza fondamentale identica ad una canna cilindrica aperta di pari lunghezza
2. Le frequenze proprie di ordine superiore stanno in rapporti armonici con la fondamentale

Esistono tuttavia alcune importanti differenze tra canne cilindriche e coniche, tutte dovute al fatto che mentre i fronti d'onda nelle canne cilindriche sono piani, quelli nelle canne coniche sono sferici. La principale conseguenza di questo fatto è perfettamente intuitiva:

• mentre una canna cilindrica è invertibile, cioè se ne possono scambiare ingresso ed uscita senza modificarne le proprietà acustiche, una canna conica non lo è. Ad esempio un megafono non funziona, se usato al contrario.

In termini più precisi possiamo dire che l'asimmetria deriva dal fatto che,

• mentre un fronte d'onda piano non cambia la sua area durante la propagazione, un fronte sferico aumenta la sua area con il quadrato della distanza dal punto d'origine.

Di conseguenza il suono subisce un'attenuazione anche in assenza di attriti e dispersioni, semplicemente dovuta al fatto che l'energia sonora proveniente dalla sorgente si deve distribuire in una regione di spazio sempre maggiore man mano che l'onda avanza. All'opposto l'energia si concentra in una regione sempre più piccola per le onde retrograde, il che fornisce il presupposto per il funzionamento, ad esempio, del cornetto acustico. Sempre per la stessa ragione si ha anche che,

• a differenza di quanto accade per le onde piane, nella propagazione entro guide coniche ad un nodo di pressione non corrisponde necessariamente un ventre di velocità, né vale il viceversa.

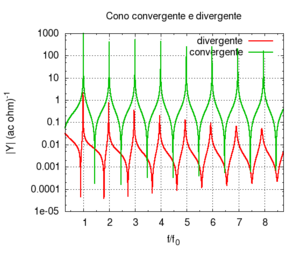
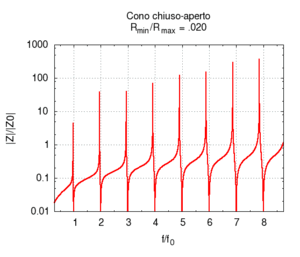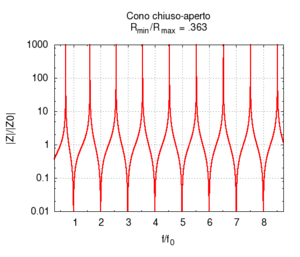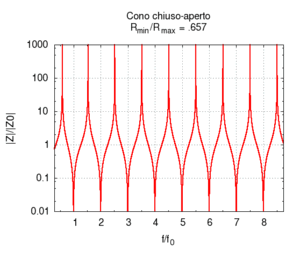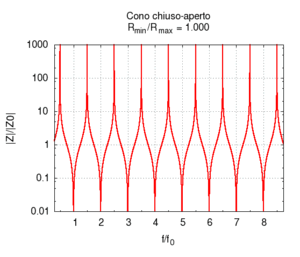
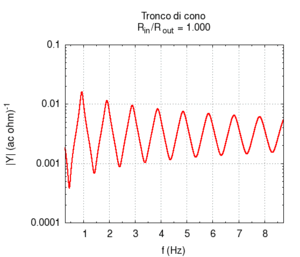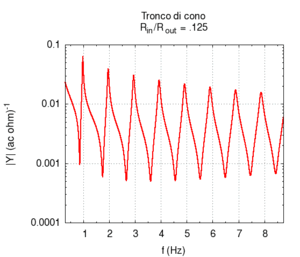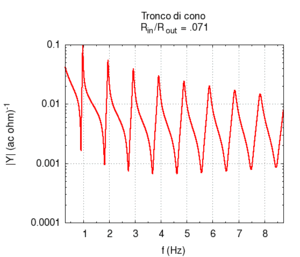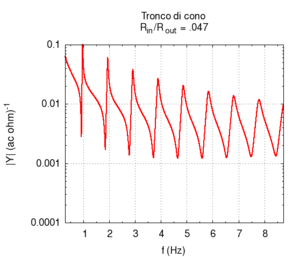
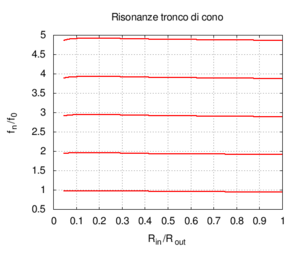
Nelle immagini che sequono studiamo come si modifica la risposta di una canna cilindrica aperta-aperta che viene trasformata in una tronco-conica allargando progressivamente l'estremità di uscita. Osservando la figura centrale, si nota che i massimi dell'ammettenza, che determinano in questo caso le frequenze di risonanza del sistema, restano sostanzialmente invariati durante la trasformazione. Ciò è di nuovo indice del fatto che la canna cilindrica iniziale e tutte le canne coniche di pari lunghezza hanno le stesse risonanze. Tuttavia si nota chiaramente il passaggio da una forma simmetrica ad una asimmetrica della risposta in frequenza. La risposta conica è "distorta" rispetto a quella cilindrica tra un massimo e l'altro, e, in genere, le antirisonanze non si trovano a metà strada tra due risonanze. Osservando l'immagine più a destra si nota infine che frequenze di risonanza rimangono sostanzialmente invariate, fatta eccezione per le piccole deviazioni dovute al maggiore irraggiamento che si ha per bocche di canna particolarmente grandi.

Geometria	Risposta acustica	Risonanze

Il paradosso della canna semichiusa

Si potrebbe a prima vista pensare che, come una canna tronco-conica (cioè aperta da entrambe le estremità) ha le stesse risonanze di una canna cilindrica aperta-aperta, così una canna conica completa (con l'estremità chiusa nel vertice, e la base aperta) corrisponda ad una canna cilindrica semi-aperta. Non è così.

• La canna conica completa (cioè chiusa-aperta) ha le stesse frequenze di risonanza della canna cilindrica aperta-aperta di pari lunghezza.

strumento	Clarinetto in Si♭	Flauto	Oboe
lunghezza canna L (cm)	66	60	65
nota più grave eseguibile	Re3 (146 Hz)	Do4 (262 Hz)	Si♭3 (233 Hz)
geometria semplificata	cilindro (chiuso-aperto)	cilindro (aperto-aperto)	cono (chiuso-aperto)
	rosso = pressione sonora; verde = velocità dell'aria
modo fondamentale
lunghezza d'onda della fondamentale	4L	2L	2L
frequenza della fondamentale	${\displaystyle f_{0}}$	${\displaystyle 2f_{0}}$	${\displaystyle 2f_{0}}$

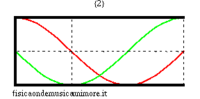
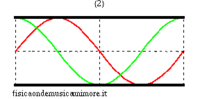
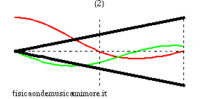
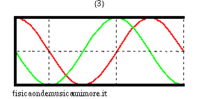
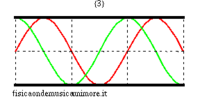
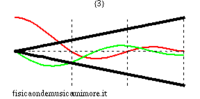
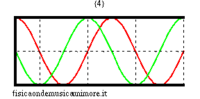
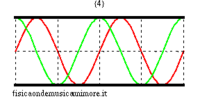
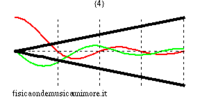
Per rendersene conto basta esaminare i modi di vibrazione nei due casi. Si vede immediatamente che le onde di pressione in ogni modo hanno nodi separati esattamente dalla stessa distanza, il che significa che la lunghezza d'onda (e quindi anche la frequenza) è la stessa, anche se la forma d'onda differisce nei due casi. Alcune animazioni dei modi di vibrazione delle canne si trovano nelle pagine modi normali di una canna cilindrica, e modi normali di una canna conica. Per uno studio avanzato si veda la pagina equazione delle onde nella canna.

modi superiori (in evidenza la posizione dei nodi)

Questo fatto spiega un'importante proprietà musicale di clarinetto, oboe e flauto: nonostante i tre strumenti abbiano all'incirca le stesse dimensioni, il clarinetto emette suoni un'ottava più bassi di quelli dell'oboe, mentre oboe e flauto suonano nella stessa tessitura. Infatti il clarinetto ha una canna cilindrica, ma l'ancia battente forza un antinodo di pressione all'imboccatura, il che la rende acusticamente equivalente ad una canna semi-chiusa (si veda in proposito la pagina sulla rifrazione nelle canne). Al contrario l'oboe ha un corpo conico, ed emette quindi una fondamentale di lunghezza d'onda pari al doppio della lunghezza dello strumento, identica a quella del flauto, che è un cilindro aperto-aperto. Il clarinetto dunque possiede una fondamentale di lunghezza d'onda pari a circa quattro volte la lunghezza dello strumento, e non due volte come oboe e flauto. Per la precisione dobbiamo dire che in realtà il corpo del clarinetto non è completamente cilindirico, ma termina con una campana conica che ne modifica un poco la risposta (si veda canna mista per alcuni esempi che illustrano questo fenomeno). Questo fatto, tuttavia, non influisce sul ragionamento fatto riguardo alla fondamentale della canna.

Di nuovo questo paradosso è frutto della natura sferica delle onde che si propagano nel condotto conico, a differenza delle onde piane che viaggiano nei condotti cilindrici.

Geometria	Risposta acustica	Risonanze
Studiamo la trasformazione dal cono completo al cilindro semiaperto. Nonostante il tipo di terminazione non cambi, mutano le condizioni al contorno della propagazione ondosa nel tubo, a causa della diversa natura geometrica delle onde. In fatti nel cono si propagano sferiche, mentre nel cilindro si propagano onde piane.	Si passa da una risposta in frequenza asimmetrica nel cono ad una simmetrica nel cilindro. In questo caso i minimi dell'ammettenza restano fissi, ma i massimi, che indicano le frequenze di risonanza si spostano sensibilmente e passano dai multipli della fondamentale a mezza onda del cono ai multipli dispari della fondamentale in quarto d'onda del cilindro semiaperto.	La fondamentale del cilindro finale si trova un'ottava sotto quella del cono iniziale, e manca delle armoniche pari.

---