Frequenze proprie e lunghezza della canna

La canna cilindrica aperta da entrambe le estremità, ma senza altri fori costituisce lo strumento a fiato modello più semplice possibile. Molte tipi di canne d'organo sono così costruite, e inoltre il modello è utile per descrivere alcune proprietà di strumenti a canna cilindrica quali il flauto o il clarinetto.

La colonna d'aria è posta in vibrazione all'interno di un tubo che sostanzialmente funge da guida per le onde sonore. Almeno per frequenze non troppo elevate le onde, provocate ad un estremo della canna da una sorgente di energia esterna, anziché propagarsi libere nello spazio in fronti d'onda sferici, sono costrette entro il tubo e si propagano parallelamente all'asse mantenendo fronti d'onda piani (per le eccezioni si veda la discussione sulle ipotesi semplificatrici, e il paragrafo seguente). Non ci occupiamo qui di descrivere nei dettagli i modi in cui è possibile mettere in oscillazione la colonna d'aria. Si vedano al proposito le pagine sui diversi strumenti a fiato.

La lunghezza finita L della canna è l'elemento chiave che la rende un risuonatore altamente selettivo, e quindi un potenziale strumento musicale. Infatti, affinché nella canna si instauri una vibrazione sostenuta per il tempo necessario a che se ne possa percepire un suono, bisogna che le onde che viaggiano avanti e indietro lungo la canna, in seguito alle riflessioni alle estremità, siano in grado di costituire un'oscillazione stazionaria. Il modo in cui si instaurano le onde stazionarie è esaminato meglio altrove (onde stazionarie, onde stazionarie in 1D), qui basti ricordare che le onde stazionarie possibili sono tutte e sole quelle che hanno il corretto comportamento alle estremità.

Qual è questo corretto comportamento? Qui il problema può rivelarsi assai complesso per gli strumenti musicali reali, in quanto l'estremità della canna è un punto in cui l'impedenza acustica cambia, passando dal valore che ha all'interno del tubo a quello che si ha in aria aperta. Nei casi reali parte dell'energia acustica viene ceduta dalla canna all'ambiente, ed anzi, è proprio questa parte che viene poi irraggiata nello spazio circostante e che possiamo percepire come suono proveniente dallo strumento. Il passaggio da una vibrazione confinata ad una libera, tuttavia può essere complesso, e ai bordi della canna i fronti d'onda possono subire diffrazione.

In estrema sintesi, il passaggio da un fronte d'onda piano ad uno sferico avviene generalmente per gradi, e attraverso geometrie complesse, e il calcolo accurato dell'effetto di questo passaggio sulle frequenze proprie della canna non è elementare. Ma qui stiamo analizzando strumenti modello, e perciò possiamo iniziare dal caso più semplice.

Canna ideale aperta-aperta

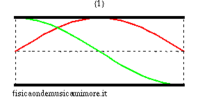
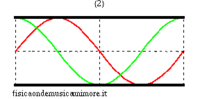
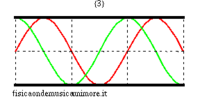
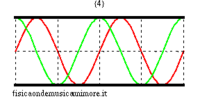
Nel caso idealizzato di canna non radiante, i possibili modi di oscillazione corrispondenti alle onde stazionarie sono del tutto analoghi a quelli della corda vibrante. Infatti l'onda di pressione ha sempre dei nodi in corrispondenza delle estremità del tubo, in quanto un nodo di pressione acustica corrisponde ad un punto in cui la pressione del mezzo resta invariata e pari alla pressione atmosferica esterna. I modi normali possono essere visualizzati quindi in analogia ai modi normali di una corda, con l'avvertenza che le figure per la corda possono riferirsi all'effettiva configurazione geometrica della corda stessa, mentre, nel caso della canna, essendo le oscillazioni della colonna d'aria longitudinali, e non trasversali, essi vanno considerati come un grafico astratto dell'andamento della pressione lungo la canna.

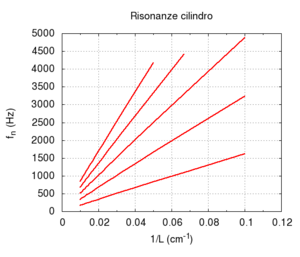
Nel caso ideale, dunque, è molto facile calcolare le frequenze proprie della canna aperta senza dover risolvere veramente l'equazione d'onda. Le frequenze dipendono solo dalla lunghezza della canna L, e dalla velocità del suono c. La minima frequenza, o fondamentale della canna, corrisponde alla massima lunghezza d'onda compatibile con i vincoli, pari al doppio della lunghezza della canna

${\displaystyle f_{0}={\frac {c}{2L}}}$,

mentre le frequenze superiori stanno in rapporto perfettamente armonico con la fondamentale

${\displaystyle f_{n}=nf_{0}\;}$.

modi normali: rosso = pressione sonora; verde = velocità dell'aria

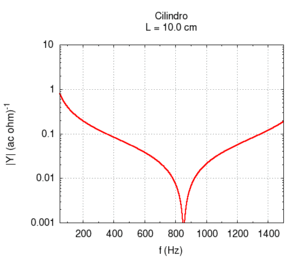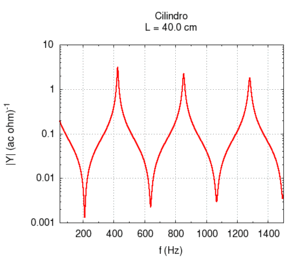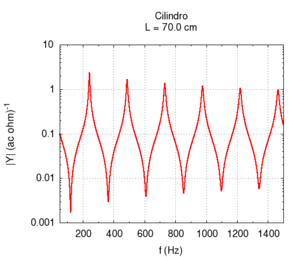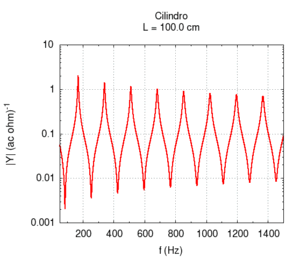
Utilizzando il linguaggio dell'impedenza, possiamo studiare in un unico grafico la risposta del sistema a tutte le frequenze. Ci aspettiamo una risposta caratterizzata da stretti picchi in corrispondenza delle frequenze di risonanza, e da un'attenuazione a tutte le altre frequenze. Nei punti intermedi tra due risonanze si ha la risposta più debole in assoluto, o antirisonanza.

Geometria	Risposta acustica	Risonanze
Studiamo la risposta di una canna ideale (senza radiazione) in funzione della sua lunghezza. La lunghezza varia tra 10 e 100 cm, mentre il raggio è costante in tutti i casi ed è pari a 1 cm.	Disegniamo il valore assoluto dell'ammettenza Y (l'inverso dell'impedenza Z). Essa descrive il rapporto tra il flusso e la pressione acustica all'ingresso della canna. L'ammettenza ha un massimo in corrispondenza delle frequenze di risonanza del sistema, perché a tali frequenze la pressione acustica all'estremità vale zero (nodo dell'onda stazionaria di pressione).	In questo grafico si mostra l'andamento delle frequenze dei primi 5 modi normali in funzione della lunghezza di canna. Le frequenze sono inversamente proporzionali alla lunghezza, quindi, disegnandole in funzione dell'inverso della lunghezza si ottengono delle rette.

Canna ideale semi-aperta

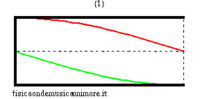
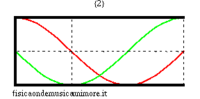
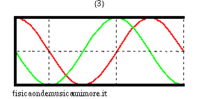
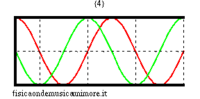
Quando la canna è chiusa da una parte, le condizioni al contorno cambiano. In particolare, come all'estremità aperta si deve avere un nodo di pressione (la pressione non cambia perché si assume l'aria esterna idealmente infinitamente cedevole), così all'estremità chiusa si deve avere un nodo di velocità (perché si assume la parete chiusa infinitamente rigida). Ma per le onde piane un nodo di pressione corrisponde sempre ad un ventre di velocità e, viceversa, un nodo di velocità corrisponde ad un ventre di pressione. Così, per la canna semiaperta, le frequenze possibili corrispondono ad onde stazionarie di pressione che hanno un ventre all'estremità chiusa, e un nodo all'estremità aperta. La più lunga di queste onde misura quattro volte la lunghezza di canna, e, detta c la velocità del suono, corrisponde alla frequenza

${\displaystyle f_{0}={\frac {c}{4L}}}$.

Le altre frequenze proprie sono multipli dispari di questa fondamentale

${\displaystyle f_{n}=(2n+1)f_{0}\;}$

Teoricamente possiamo anche studiare il caso di una canna chiusa-chiusa, ma questo non ha particolare interessa acustico, in quando non permette irraggiamento del suono nell'ambiente circostante.

modi normali: rosso = pressione sonora; verde = velocità dell'aria

Effetto di attriti e irraggiamento

Studiamo ora canne un po' meno ideali, introducendo, uno per volta, gli effetti dovuti all'attrito viscoso e all'irraggiamento del suono da parte della canna. Per fissare le idee ci riferiamo ad una canna aperta-aperta, ma le conclusioni generali si applicano ugualmente agli altri casi.

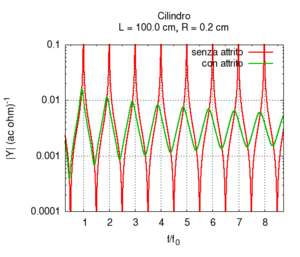
Si noti che il grafico dell'ammettenza dà maggiori informazioni sulla risposta della canna rispetto alla sola conoscenza delle frequenze di risonanza. In particolare si noti che l'ammettenza alle alte frequenze è progressivamente minore dell'ammettenza alle basse frequenze. In altre parole le frequenze più alte tendono ad essere maggiormente attenuate rispetto alle frequenze basse. Questo comportamento è in parte dovuto alla presenza di attrito viscoso tra il flusso dell'aria e le pareti della canna. L'attrito viscoso dipende dalla velocità del flusso, e, dallo studio della risonanza sappiamo che esso influenza fortemente l'ampiezza dei picchi, e, debolmente, anche la loro posizione.

Una canna del tutto ideale (cioè senza attrito) avrebbe picchi tutti uguali, e di valore infinito in corrispondenza delle risonanze. Tutte le canne reali tuttavia disperdono parte dell'energia acustica in attriti, e infatti, paragonando le due risposte disegnate nella figura a lato si nota che, oltre all'attenuazione, la presenza di attrito viscoso determina anche un piccolo spostamento delle frequenze di risonanza verso il basso. Tale spostamento, tuttavia, non è lo stesso per tutte le frequenze, il che implica che, in presenza di attriti, la risposta della canna non è esattamente armonica. Le deviazioni sono comunque molto piccole. Nell'esempio si è scelta una canna di piccolo diametro perché naturalmente, in tale condizione l'effetto degli attriti è più rilevante.

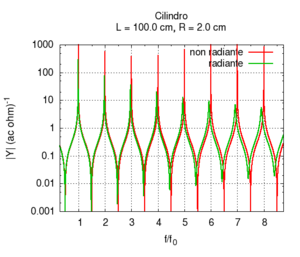
Al contrario di quanto avviene per l'attrito l'irraggiamento di onde sonore nell'ambiente è favorito quando la canna è di grande diametro. In tale situazione, infatti, i fronti d'onda piani all'estremità della canna approssimano bene quelli sferici che si hanno nell'aria aperta. Si può dire che l'impedenza della canna è meglio adattata all'impedenza di radiazione. Nell'esempio qui accanto si può osservare che l'irraggiamento produce una forte attenuazione alle alte frequenze, tuttavia la forma dei picchi è meno "smussata", e resta più simile a quella ideale.

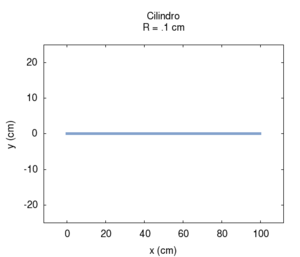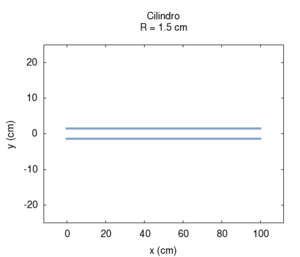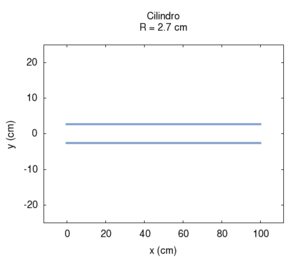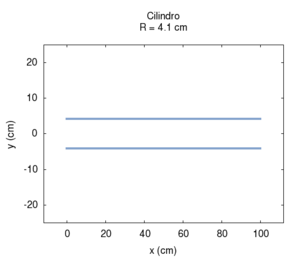
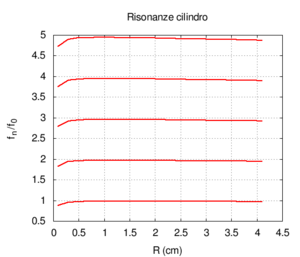
Naturalmente nelle canne reali sia l'irraggiamento, sia l'attrito contribuiscono alla risposta dello strumento simultaneamente. Questo caso è meglio illustrato nei disegni che seguono, in cui la risposta della canna è calcolata a lunghezza fissata, ma a diametro variabile, ed entrambe le correzioni per attrito e irraggiamento sono applicate. Osservando l'immagine più a destra con la posizione delle risonanze si nota una larga regione sostanzialmente piatta, ai cui estremi si hanno deviazioni, dovute soprattutto agli attriti per raggi piccoli, e all'irraggiamento per raggi grandi. Il grafico dell'ammettenza mostra un progressivo aumento di tutti valori all'aumentare del raggio. Questo è prevedibile, in quanto una canna di grande calibro oppone minor resistenza di una di piccolo calibro. Anche la forma dei picchi, molto "smussati" per raggi piccoli, a causa del forte attrito, assomiglia sempre più alla risposta ideale non smorzata per raggi grandi. Si può anche notare lo spostamento delle frequenze prima verso l'alto, per effetto del diminuito attrito, poi leggermente verso il basso, specie nelle armoniche di ordine maggiore. Tale spostamento è meglio evidenziato nell'immagine più a destra.

Geometria	Risposta acustica	Risonanze

---
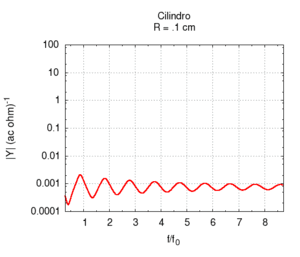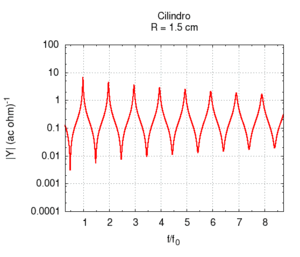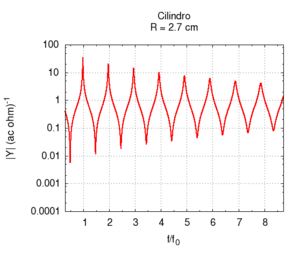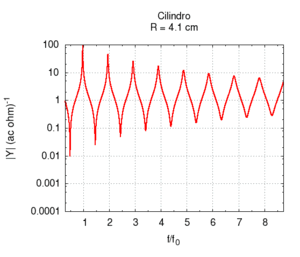