Canna cilindrica con terminazione conica

La maggior parte degli strumenti a fiato reali ha una geometria complessa. Molti di essi, come la tromba o il clarinetto, tuttavia, presentano una canna che può essere ben approssimata dalla giunzione di due tratti, uno cilindrico e uno conico. Rimanendo nell'ambito degli strumenti modello, dunque è interessante studiare la risposta di canne con questa geometria variandone separatamente i due possibili parametri, e cioè

1. la lunghezza relativa del tratto cilindrico e di quello conico fissato il raggio terminale di quest'ultimo
2. l'ampiezza della bocca del cono, fissata la posizione di innesto sul cilindro.

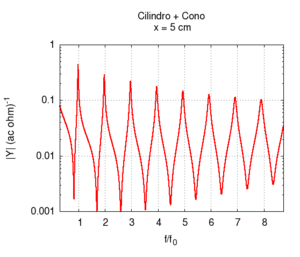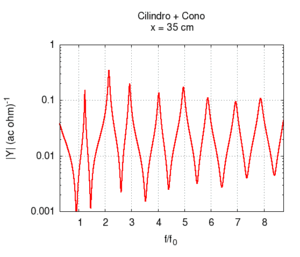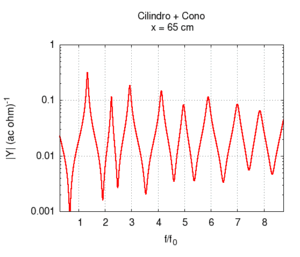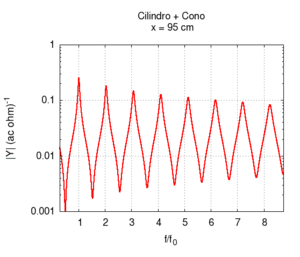
I grafici che seguono mostrano il risultato del calcolo approssimato della risposta, e ci permettono di trarre alcune considerazioni.

Innanzitutto è evidente che la giunzione dei due tratti produce risposte varie ed interessanti, rispetto alle geometrie più semplici, il che spiega, almeno in parte, la varietà timbrica che è possibile ottenere dai fiati. In entrambi i casi si nota che la variazione continua di un solo parametro produce effetti su tutto lo spettro, e non su una sola componente. Questo fatto suggerisce che la progettazione "a tavolino" del suono di una canna, per quanto semplice sia la sua geometria, non è cosa semplice. In particolare si osserva che variazioni anche piccole possono influire sia sulla posizione della fondamentale, sia sui mutui rapporti tra le frequenze delle armoniche superiori e della fondamentale.

Il primo effetto non è particolarmente importante, in quanto determina uno spostamento nell'intonazione base dello strumento, spostamento cui si può sempre porre rimedio correggendo la lunghezza complessiva della canna.

Il secondo effetto è più interessante, in quanto può influire sul grado di anarmonicità dello strumento. Questo fatto, a sua volta, influisce sul timbro dello strumento sia in senso fisico, sia attraverso il meccanismo della percezione, che è in grado di cogliere in modo sottile l'armonicità o meno di un suono complesso. Per la discussione di questo tema si rimanda però alle relative pagine nella sezione dedicata alla percezione del suono.

Geometria	Risposta acustica	Risonanze
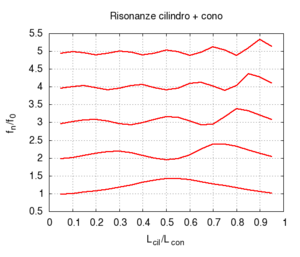
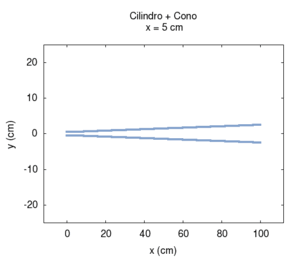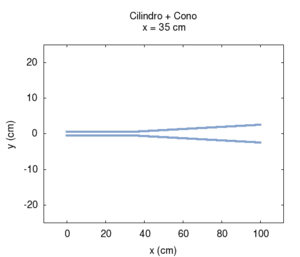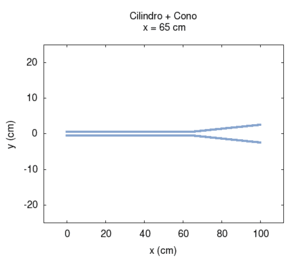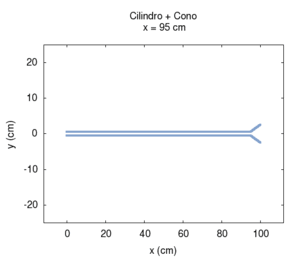
Variando la mutua lunghezza del tratto cilindrico rispetto a quello conico si passa gradualmente da uno strumento puramente conico ad uno puramente cilindrico attraverso una serie di passi intermedi. Conosciamo già lo spettro degli estremi, e sappiamo in particolare che essi hanno le stesse frequenze di risonanza (si veda in proposito canna cilindrica e canna conica). Ora possiamo apprezzare però il fatto che la transizione delle frequenze non è uniforme. La fondamentale cresce, e poi torna al valore iniziale in modo non lineare in funzione della posizione di inizio del tratto conico, mentre le armoniche superiori oscillano passando per un numero di massimi pari all'ordine dell'armonica più uno. La prima armonica ha due massimi, la seconda tre, e così via. Esistono punti in cui la sere è più armonica di altri, ma solo agli estremi è esattamente armonica.

Geometria	Risposta acustica	Risonanze
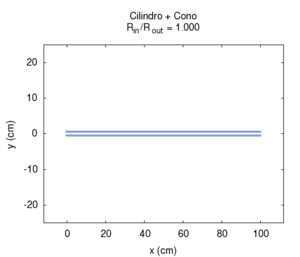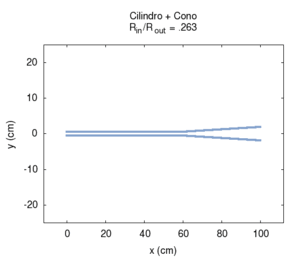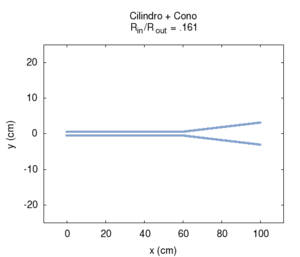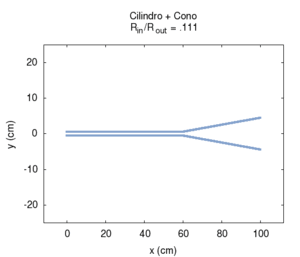
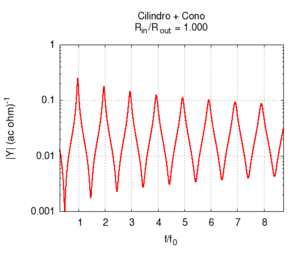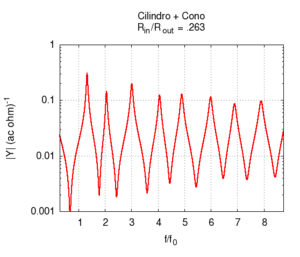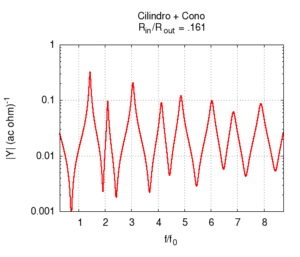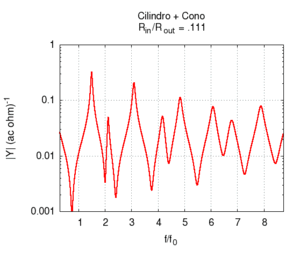
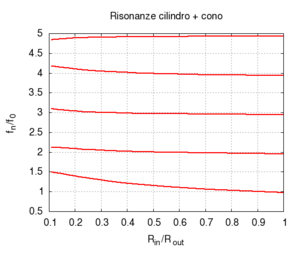
L'effetto della campana è particolarmente importante negli ottoni, e non può essere interamente descritto in termini del nostro semplice modello. Comunque già per la geometria semplificata del disegno possiamo fare alcune osservazioni utili. In primo luogo la campana adatta l'impedenza della canna all'impedenza dell'aria libera, facilitando così l'irraggiamento del suono. Questo irraggiamento è particolarmente facilitato alle alte frequenze, il che contribuisce a dare agli ottoni un suono particolarmente squillante, anche quando la fondamentale emessa è piuttosto grave, come accade negli strumenti di grosse dimensioni (trombone, basso tuba, ecc.). All'aumentare dell'apertura della campana l'impedenza all'estremità della canna diminuisce, favorendo l'attenuazione delle armoniche pari, e la risposta dello strumento diviene sempre meno armonica. Bisogna tuttavia notare che gli ottoni moderni, a differenza dei corrispondenti strumenti antichi, non hanno campane coniche, ma sagomate secondo curve più complesse, per le quali si rende necessaria un'analisi più accurata.

---