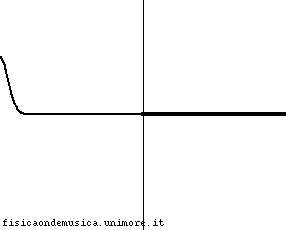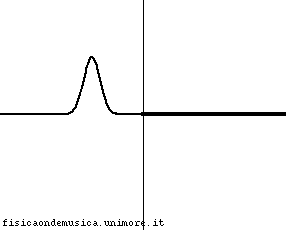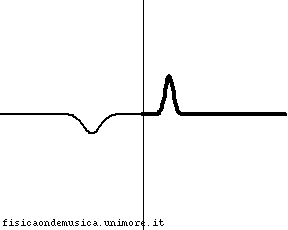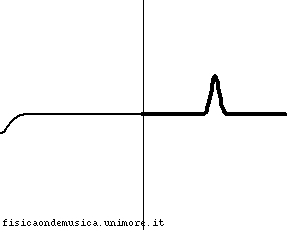Una situazione modello

Il concetto di impedenza diviene particolarmente utile quando si vuole studiare il trasferimento di energia da un mezzo ad un altro utilizzando la proprietà più caratteristica delle onde, e cioè la loro capacità di propagarsi. In modo informale possiamo dire che l'impedenza è una grandezza fisica che descrive sinteticamente quanto un mezzo "si oppone" alla propagazione delle onde. L'impedenza, nel caso più generale, si esprime come un coefficiente di proporzionalità e uno sfasamento che lega tra loro due grandezze il cui prodotto ha le dimensioni di un lavoro per unità di tempo, come forza e velocità.

Per essere più precisi dobbiamo riferirci ad un esempio, e scegliamo un caso simile a quello illustrato in dettaglio nella pagina rifrazione nelle corde, e cioè il caso in cui facciamo propagare un impulso meccanico lungo due tratti di corda di densità diversa congiunti in un punto. Questo caso particolare non ha vere applicazioni pratiche, ma si presta particolarmente ad illustrare il fenomeno. Le applicazioni sono riprese nel paragrafo successivo.

Consideriamo quindi due corde ideali di densità ρ₁ e ρ₂ unite in un punto, e sottoposte ad una tensione T. Lungo di esse facciamo viaggiare un'onda trasversale, come nell'animazione qui accanto. Per avere un'idea intuitiva dell'andamento del fenomeno si vedano le animazioni e i commenti alla pagina rifrazione nelle corde.

L'impedenza specifica della corda è la grandezza Z che lega la tensione della corda alla velocità di propagazione delle onde nella corda nel modo seguente

${\displaystyle Z={\frac {T}{v}}}$.

Data l'ampiezza A di un'onda che si propaga lungo la corda, l'energia che l'onda trasporta con sé nell'unità di tempo è

${\displaystyle E\propto ZA^{2}\,}$.

Rimandiamo alla pagina sull'impedenza di una corda vibrante per la derivazione completa dell'espressione matematica dell'impedenza della corda, e concentriamoci sul risultato finale. Per i nostri due tratti di corda avremo

${\displaystyle Z_{1}={\frac {T}{v_{1}}}}$,

${\displaystyle Z_{2}={\frac {T}{v_{2}}}}$.

Si noti che quanto minore è l'impedenza della corda tanto più velocemente viaggia lungo essa l'onda meccanica.

Possiamo ora introdurre i coefficienti di trasmissione e riflessione, che ci dicono quale ampiezza avranno le onda trasmessa e riflessa, data l'ampiezza dell'onda incidente.

• Il coefficiente di trasmissione è il rapporto tra l'ampiezza dell'onda trasmessa e quella dell'onda incidente

${\displaystyle C_{T}={\frac {A_{t}}{A_{i}}}={\frac {2v_{2}}{v_{1}+v_{2}}}}$.

• Il coefficiente di riflessione è il rapporto tra l'ampiezza dell'onda riflessa e quella dell'onda incidente

${\displaystyle C_{R}={\frac {A_{r}}{A_{i}}}={\frac {v_{2}-v_{1}}{v_{1}+v_{2}}}}$.

La derivazione completa dei coefficienti, in termini delle velocità di propagazione nei due tratti di corda si trova alla pagina coefficienti di trasmissione e riflessione.

Possiamo ora esprimerli in termini delle impedenze, sostituendo le variabili, ed otteniamo

${\displaystyle C_{T}={\frac {2Z_{1}}{Z_{1}+Z_{2}}}}$.

(1)

e

${\displaystyle C_{R}={\frac {Z_{1}-Z_{2}}{Z_{1}+Z_{2}}}}$.

(2)

L'interesse di questa sostituzione non è evidente a questo punto, ma lo diventa immediatamente se, anziché focalizzarci sull'ampiezza dell'onda riflessa e trasmessa, studiamo la quantità di energia che è trasmessa e riflessa dal punto di giunzione nell'unità di tempo.

Se infatti ricordiamo che l'energia di un'onda armonica è proporzionale al quadrato della sua ampiezza (si veda energia trasportata dall'onda ed energia della corda vibrante) chiamando E_i, E_r ed E_t rispettivamente le quantità di energia incidente, riflessa e trasmessa dalla giunzione, abbiamo che

${\displaystyle {\frac {E_{r}}{E_{i}}}={\frac {Z_{1}A_{r}^{2}}{Z_{1}A_{i}^{2}}}}$,

${\displaystyle {\frac {E_{t}}{E_{i}}}={\frac {Z_{2}A_{t}^{2}}{Z_{1}A_{i}^{2}}}}$,

da cui, sostituendo (1) e (2),

${\displaystyle {\frac {E_{r}}{E_{i}}}=\left({\frac {Z_{1}-Z_{2}}{Z_{1}+Z_{2}}}\right)^{2}}$,

(3)

${\displaystyle {\frac {E_{t}}{E_{i}}}={\frac {4Z_{1}Z_{2}}{(Z_{1}+Z_{2})^{2}}}}$.

(4)

Osservando la forma matematica della (3) e della (4) è possibile accorgersi che, se Z₁ e Z₂ sono molto diverse tra loro non è possibile trasferire efficacemente l'energia da un mezzo all'altro.

Infatti, sia nel caso ${\displaystyle Z_{1}\gg Z_{2}\,}$, sia in quello ${\displaystyle Z_{1}\ll Z_{2}\,}$, si ha

${\displaystyle {\frac {E_{r}}{E_{i}}}\approx 1}$,

${\displaystyle {\frac {E_{r}}{E_{i}}}\approx 0}$.

In altre parole, quando due mezzi hanno impedenze molto differenti, l'energia, da qualunque parte essa provenga, sarà quasi interamente riflessa all'interfaccia, senza riuscire a trasferirsi all'altro mezzo.

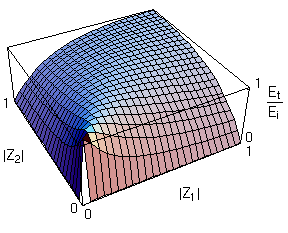
Osservando il grafico del rapporto tra E_t ed E_i riportato qui a fianco si nota inoltre che il coefficiente di trasferimento dell'energia è sempre massimo quando Z₁=Z₂ per qualunque valore di Z₁ e Z₂. Di conseguenza il massimo dell'efficacia in trasmissione si ottiene solo quando i due mezzi hanno la stessa impedenza. Si vede anche che il massimo è piuttosto "largo", e, in particolare, questo significa che, al crescere delle impedenze, per ottenere un buon trasferimento, è sufficiente che Z₂ e Z₂ siano "non troppo differenti".

Ecco dunque il problema tecnologico fondamentale illustrato dalla nostra situazione modello:

come trasmettere l'energia tra due mezzi aventi impedenze specifiche molto differenti?

La risposta è una tecnica nota come adattamento di impedenza.

Adattamento e adattatori

Il concetto chiave è il seguente: inserire un terzo mezzo tra i due originali di impedenza e dimensioni appropriate tali che l'impedenza del mezzo 1 unito al mezzo 3 sia molto simile a quella del mezzo 2, o, che è lo stesso, tali che l'impedenza del mezzo 2 unito al mezzo 3 sia molto simile a quella del mezzo 1. Nel nostro esempio l'adattatore sarà semplicemente un pezzo di una corda di densità e lunghezza appropriata.

La condizione di adattamento ideale si ottiene quando le impedenze del mezzo 1+3 (chiamiamolo 1') e del mezzo 2 sono identiche ${\displaystyle Z_{1'}=Z_{2}\,}$. Quando questo accade si vede facilmente dalle (3) e (4) che

${\displaystyle {\frac {E_{r}}{E_{i}}}=0}$,

mentre

${\displaystyle {\frac {E_{t}}{E_{i}}}=1}$,

cioè i due mezzi sono "trasparenti" l'uno all'altro, e tutta l'energia è libera di fluire dal primo al secondo e viceversa.

Ora che la trasmissione o la riflessione delle onde tra due mezzi è espressa in termini delle impedenze possiamo vedere facilmente che, attraverso l'analogia fisica, lo stesso ragionamento, si può in realtà applicare a molti ambiti differenti. In ciascun caso l'energia coinvolta avrà un'espressione differente, e così l'impedenza specifica del mezzo, ma il principio dell'adattamento rimane lo stesso.

Esempi meccanici ed acustici

• Adattamento dell'impedenza meccanica negli strumenti musicali

Pensiamo agli strumenti a corda. Quando ne sentiamo il suono esso è trasportato dall'aria. Tuttavia lo strumentista non eccita direttamente l'aria, come invece accade per gli strumenti a fiato. Egli mette in vibrazione una o più corde, che, a loro volta mettono in vibrazione una superficie di legno (una tavola che fa parte del corpo dello strumento), che, infine, agisce sull'aria. Abbiamo una catena di tre sistemi, ciascuno con una sua impedenza specifica. In particolare, accade che l'impedenza delle corde sia molto minore di quella della tavola. Ecco che serve un adattatore di impedenza tra le due. Esso è in genere costituito da un "ponticello" di legno, su cui le corde sono tese. Il ponticello riceve la vibrazione delle corde, e "fa leva" con i suoi piedi sulla tavola, effettivamente adattando l'impedenza dei due sistemi, e permettendo l'eccitazione della tavola a partire da quella delle corde.

• Adattamento di impedenza acustica sonda ecografica-pelle tramite gel

L'impedenza acustica di un mezzo è data dal prodotto tra la densità del mezzo e la velocità con cui in esso si propaga il suono. Di conseguenza è facile vedere che aria e acqua hanno impedenze completamente non adatte a trasmettere mutuamente le onde sonore, perché l'acqua ha impedenza di molto superiore a quella dell'aria (al proposito si veda anche la discussione riguardante la rifrazione del suono. Infatti, per il funzionamento di apparecchiature di diagnosi basate sugli ultrasuoni è impossibile inviare gli ultrasuoni sul paziente in aria, ma bisogna avvalersi di un emettitore posto a contatto col corpo del paziente, e utilizzare un gel per meglio adattare le impedenze dell'emettitore e del corpo umano. Per lo stesso motivo le cavità interne del corpo che contengono aria sono completamente opache agli ultrasuoni, che vengono sempre totalmente riflessi alla superficie di separazione tra aria e acqua.

Lo stesso discorso trova applicazione nell'acustica sottomarina, in cui è importante adattare le impedenze di emettitori e microfoni (in genere di acciaio) a quella dell'acqua per potervi spedire e ricevere segnali sonori.

• Adattamento dell'impedenza nell'apparato uditivo

Come meglio illustrato nella pagina sull'anatomia del sistema uditivo un problema molto simile a quello precedente si ha nella trasformazione dell'energia acustica in meccanica che avviene all'interno dell'orecchio. Alle due estremità della catena di trasduzione si trova da una parte l'aria, che veicola le onde sonore, e dall'altra la coclea, che contiene un liquido che costituisce l'ultimo stadio in cui il suono è ancora energia meccanica all'interno del corpo umano. La vibrazione del liquido infatti eccita cellule ciliate, dalle quali il segnale non esce più come oscillazione meccanica, ma come impulso elettrico. Il complesso meccanismo di membrane (timpano), leve (ossicini) e muscoli che si interpone tra questi due punti estremi altro non è che un elaborato adattatore di impedenza che rende possibile il passaggio dell'energia tra i due mezzi (aria e liquido endolinfatico) altrimenti impossibile.

Esempi elettromagnetici

• Il film antiriflesso a quarto d'onda sulle lenti (vedi l'Applet Onde 2D per una simulazione interattiva del fenomeno).

Si tratta di un adattamento di impedenza ottica. Le onde e l'energia coinvolte sono di natura elettromagnetica. Si vuole sostanzialmente ridurre il coefficiente di riflessione ottico di una lente in un certo ambito dello spettro (per esempio il visibile). Questo rende la lente "più trasparente" in quella regione dello spettro. Questa tecnica riveste una particolare importanza nelle applicazioni ai telescopi astronomici, perché ne migliora l'efficienza e aumenta il contrasto delle immagini. L'adattatore è un film sottile che si applica sulla lente, e che produce interferenza distruttiva tra i raggi riflessi. Si può dimostrare che la condizione di adattamento di impedenza quando il film è spesso un (multiplo di) un quarto della lunghezza d'onda di cui si vuole eliminare la riflessione è

${\displaystyle {\frac {Z_{1}}{Z_{3}}}={\frac {Z_{3}}{Z_{2}}}}$,

ovvero

${\displaystyle Z_{3}={\sqrt {Z_{1}Z_{2}}}}$.

Lo stesso valore (detto media geometrica di Z₁ e Z₂) si può utilizzare anche per il nostro esempio della corda nel primo paragrafo. Ovviamente la definizione di Z cambia, ma non la condizione di adattamento!

• Adattamento microfono-amplificatore, amplificatore-altoparlante, ecc.

Qualunque circuiti elettrico può essere in ultima analisi visto come una "scatola" con quattro terminali: due in ingresso e due in uscita. Anche senza sapere cosa contiene esattamente la scatola, possiamo misurarne le impedenze elettriche in ingresso e in uscita. Quando vogliamo collegare un circuito ad un altro non facciamo altro che connettere i due terminali di uscita del primo circuito con i due di ingresso del secondo. Ecco dove si può applicare il nostro principio dell'adattamento. Sappiamo infatti che, se le impedenze del primo e del secondo circuito non sono adattate, gran parte della potenza immessa nel primo circuito sarà riflessa anziché essere trasmessa al secondo. Nei sistemi microfono-amplificatore e amplificatore-altoparlante questo punto è cruciale, perché il trasferimento ottimale della potenza diminuisce il rischio che il segnale venga distorto, e quindi consente all'impianto di lavorare con la massima fedeltà.

---