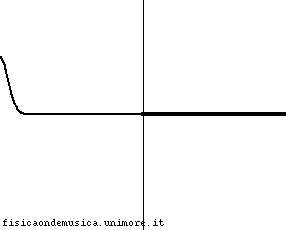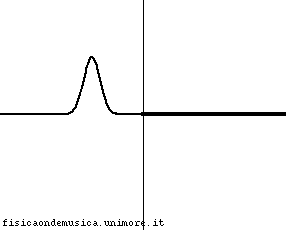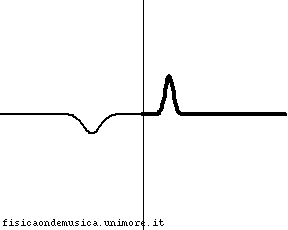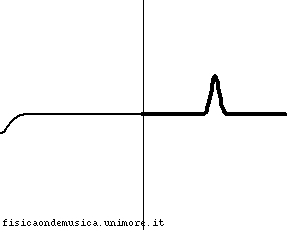Rifrazione delle onde in una corda

• Consideriamo due tratti di corde di diversa densità saldate l'una di seguito all'altra. Facciamo un piccolo sforzo di astrazione immaginando che entrambi le corde siano ideali, e che la giunzione sia una saldatura anch'essa ideale. Questo sforzo è ricompensato dal fatto che tutti i calcoli sono più semplici in queste ipotesi. Per esempio, possiamo dire che la tensione T è la stessa lungo tutta la corda composta risultante.
• Le onde si muovono con velocità diverse nelle due corde prese separatamente, infatti (vedi equazione delle onde nella corda, frequenze proprie della corda e velocità delle onde meccaniche), dette ρ₁ e ρ₂ le rispettive densità, abbiamo

${\displaystyle v_{1}={\sqrt {\frac {T}{\rho _{1}}}}}$

;

${\displaystyle v_{2}={\sqrt {\frac {T}{\rho _{2}}}}}$

Ora consideriamo un'onda trasversale che percorra la corda composta dal tratto di tipo 1 verso il tratto di tipo 2. Essa attraverserà il primo tratto con velocità v₁, ma, giunta alla saldatura, essa è costretta a cambiare improvvisamente velocità. Si ha un tipico caso di rifrazione. Al punto di discontinuità l'onda è in parte riflessa e in parte trasmessa. La sua energia quindi è ridistribuita tra le corde.

Vogliamo calcolare quale ampiezza avranno l'onda riflessa e l'onda trasmessa, data l'onda incidente.

Consideriamo dapprima, per semplicità di calcolo, onde armoniche, e poniamo l'origine delle coordinate x=0 nel punto di giunzione. Dette v₁, v₂ i valori assoluti delle velocità di propagazione rispettivamente nella corda 1 e 2, e ω la pulsazione dell'onda distinguiamo

1. onda incidente: si propaga solo verso destra nella corda 1 con ampiezza A_i

   ${\displaystyle y_{i}(x,t)=A_{i}\sin(\omega t-k_{1}x)\;}$

2. onda trasmessa: si propaga solo verso destra nella corda 2 con ampiezza A_t

   ${\displaystyle y_{t}(x,t)=A_{t}\sin(\omega t-k_{2}x)\;}$

3. onda riflessa: si propaga solo verso sinistra nella corda 1 con ampiezza A_r

   ${\displaystyle y_{r}(x,t)=A_{r}\sin(\omega t+k_{1}x)\;}$

• Per risolvere il problema abbiamo ora bisogno di equazioni che leghino le grandezze note A_i, v₁, v₂ a quelle incognite A_t e A_r. Queste equazioni si possono ricavare dalla fisica del problema:

1. la corda deve rimanere continua alla giunzione durante il moto, quindi lo spostamento dell'estremità destra della corda 1 deve essere lo stesso dell'estremità di sinistra della corda 2. Questa condizione impone che la somma delle onde incidente e riflessa sia uguale all'onda trasmessa nel punto di giunzione x=0

   ${\displaystyle A_{i}\sin(\omega t)+A_{r}\sin(\omega t)=A_{t}\sin(\omega t)\;}$.

   Poiché questa condizione deve valere indistintamente per tutti gli istanti di tempo, essa si riduce a

   ${\displaystyle A_{i}+A_{r}=A_{t}\,}$.

   (1)

2. Anche la velocità trasversale dei due tratti di corda nel punto di contatto deve essere la stessa. Purtroppo, però, questa condizione geometrica non è matematicamente indipendente dalla precedente, in quanto la pulsazione di tutte le onde sulla corda è la stessa, e quindi, la condizione è stata automaticamente verificata nel momento stesso in cui abbiamo usato una sola ω. Per imporre una condizione indipendente possiamo osservare che anche l'inclinazione della corda (cioè la derivata rispetto ad x) deve essere continua alla giunzione. Derivando rispetto ad x, quindi, e imponendo l'eguaglianza a tutti i tempi si ottiene

   ${\displaystyle -k_{1}A_{i}+k_{1}A_{r}=-k_{2}A_{t}\,}$,

   o anche, ricordando che ${\displaystyle {\frac {\omega }{k_{1}}}=v_{1}\,}$ e ${\displaystyle {\frac {\omega }{k_{2}}}=v_{2}\,}$

   ${\displaystyle {\frac {A_{i}}{v_{1}}}-{\frac {A_{r}}{v_{1}}}={\frac {A_{t}}{v_{2}}}}$.

   (2)

Incidentalmente osserviamo che questa condizione può anche essere imposta per via dinamica, in quanto e la giunzione è ideale, cioè si riduce ad un punto con massa nulla,la forza trasversale dalla parte della corda 1 deve essere uguale alla forza dalla parte della corda 2. Se così non fosse una forza finita su una massa nulla produrrebbe un'accelerazione infinita. Ricordando che

${\displaystyle F_{y}=-T\sin \theta \approx -T\tan \theta =-T{\frac {\partial y}{\partial x}}}$

(si veda equazione delle onde nella corda), si vede come la derivata rispetto ad x compaia anche dal ragionamento dinamico.

Utilizzando le equazioni (1) e (2) siamo ora in grado di ricavare i coefficienti desiderati di trasmissione C_T e di riflessione C_R.

• Il coefficiente di trasmissione è il rapporto tra l'ampiezza dell'onda trasmessa e quella dell'onda incidente

${\displaystyle C_{T}={\frac {A_{t}}{A_{i}}}={\frac {2v_{2}}{v_{1}+v_{2}}}}$.

(3)

• Il coefficiente di riflessione è il rapporto tra l'ampiezza dell'onda riflessa e quella dell'onda incidente

${\displaystyle C_{R}={\frac {A_{r}}{A_{i}}}={\frac {v_{2}-v_{1}}{v_{1}+v_{2}}}}$.

(4)

Come utile verifica si osservi che:

• C_T può solamente essere positivo: il segno della velocità di ogni onda sta nel segno usato entro la funzione seno, mentre v₁ e v₂ sono i valori assoluti
• C_R invece può avere qualunque segno. Quando è positivo indica che l'onda riflessa è in fase con quella trasmessa, mentre quando è negativo, significa che essa è in opposizione di fase. In particolare, se v₁>v₂ si ha sempre C_R<0, mentre se v₁<v₂ si ha sempre C_R>0.
• Se ${\displaystyle v_{1}\gg v_{2}\,}$ significa che il punto di giunzione è praticamente immobile, e si comporta come un estremo fisso. L'onda incidente tende ad essere completamente riflessa con inversione di fase (C_R=-1 e C_T=0).
• Se ${\displaystyle v_{1}\ll v_{2}\,}$ significa che il tratto di corda 2 ha massa trascurabile, e l'estremo si comporta come fosse libero. L'onda incidente tende ad essere di nuovo completamente riflessa, ma in concordanza di fase (C_R=1). Il valore C_T=2 in questo caso non ha un significato fisico.
• Se v₁=v₂ significa che i due tratti di corda hanno la stessa massa, e il punto di giunzione diviene un punto qualsiasi della corda. L'onda incidente viene completamente trasmessa (C_R=0 e C_T=1).

La pagina rifrazione nelle corde contiene una galleria di animazioni che illustrano questi casi limite, ed altri casi intermedi.

---