Generalità

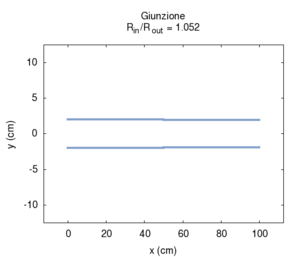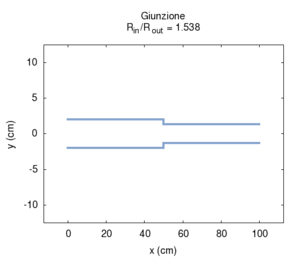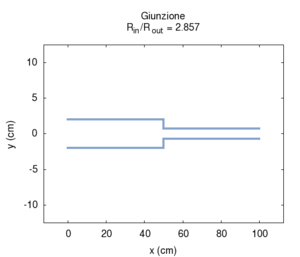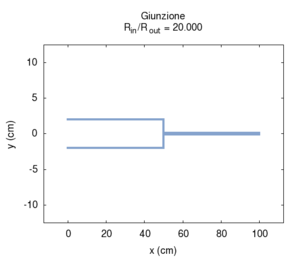
Le leggi della rifrazione e il concetto di adattamento di impedenza si possono anche applicare alla propagazione acustica alla giunzione tra due canne cilindriche di diverso diametro.

Quando un'oscillazione acustica si propaga lungo la canna si ha una differenza di pressione tra elementi contigui del gas contenuto nella canna, e, in corrispondenza, un flusso delle molecole del fluido. A differenza di quanto accadrebbe per il flusso idraulico entro i tubi, entrambe queste grandezze sono oscillanti, e quindi non si verifica un trasporto macroscopico della massa del fluido lungo la condotta, ma solo un avanzamento temporaneo, seguito da un ritorno alla posizione d'equilibrio, una retrocessione, di nuovo un ritorno all'equilibrio, e così via. Ciononostante, lungo la condotta continuano a valere le condizioni di continuità. Ad esempio, la massa d'aria che passa da una sezione piccola ad una più grande attraversando il punto di giunzione deve rimanere costante. Poiché al puhto di giunzione la portata del condotto aumenta improvvisamente, affinché la massa si conservi, si deve verificare una corrispondente diminuzione della velocità del flusso.

Cerchiamo di chiarire il processo attraverso alcuni esempi.

Esempi

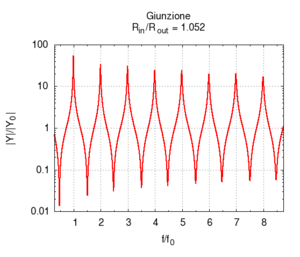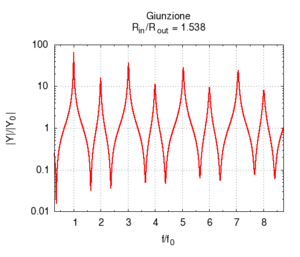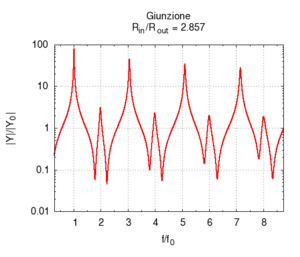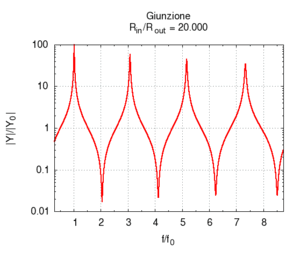
Per fissare le idee abbiamo costruito due esempi in cui un tratto di canna di 50 cm e raggio 2 mm è congiunto con un altro tratto pure lungo 50 cm, ma a raggio variabile.

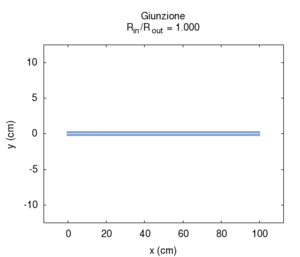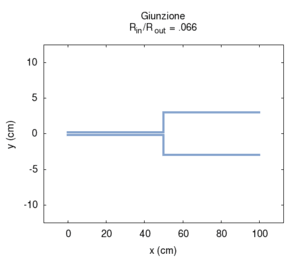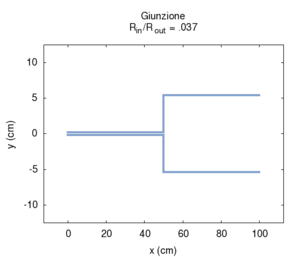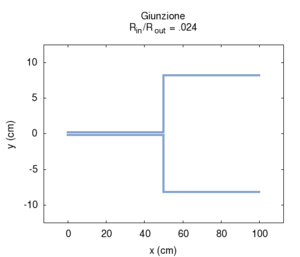
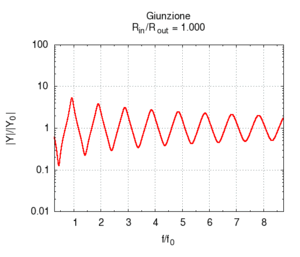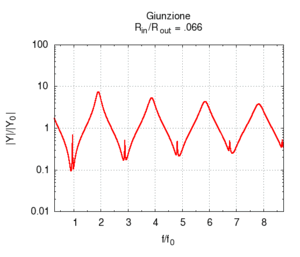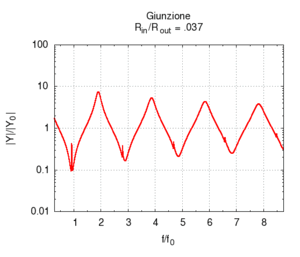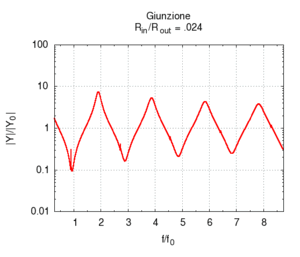
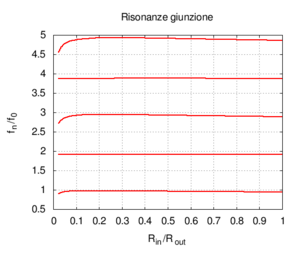
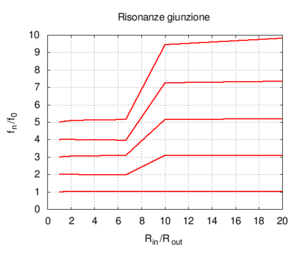
Se aumentiamo progressivamente il raggio del secondo tratto di canna passiamo progressivamente da una canna lunga 100 cm e raggio 2 mm, ad una situazione in cui una canna lunga 50 cm è congiunta ad una canna più grande, e, al limite, quando il rapporto tra i raggi ${\displaystyle R_{1}}$ e ${\displaystyle R_{2}}$ è molto piccolo (cioè il secondo tratto è molto più largo del primo), abbiamo semplicemente una canna di 50 cm che sfocia sostanzialmente in uno spazio aperto. Come si vede esaminando il grafico dell'ammettenza, le risonanze corrispondenti ai multipli dispari della frequenza fondamentale della canna da 100 cm progressivamente spariscono, e la risposta tende a diventare uguale a quella di una canna aperta-aperta di soli 50 cm. La fondamentale quindi sale di un'ottava. Il grafico a destra, che mostra l'andamento delle risonanze mostra che i valori relativi dei massimi dell'ammettenza cambiano ben poco, anche se l'esame delle ampiezze mostra che i picchi pari sono tutti fortemente attenuati già per rapporti tra i diametri pari a 1/5.

Naturalmente, quando il raggio del secondo tratto diviene molto maggiore della lunghezza d'onda che attraversa la canna la nostra semplice approssimazione unidimensionale cade, in quanto l'onda piana all'uscita dal tratto più stretto subisce diffrazione, e si tramuta in un'onda sferica nel tratto più largo. (Al proposito si veda anche l'esperienza sulla diffrazione nel laboratorio interattivo)

Geometria	Risposta acustica	Risonanze
All'inizio il sistema corrisponde ad un'unica canna di lunghezza 100 cm e raggio 2 mm. Alla fine equivale fisicamente ad una canna aperta-aperta di 50 cm e raggio 2 mm.	Le frequenze multiple dispari della fondamentale sono fortemente attenuate già per rapporti tra i raggi pari a 1/5.	Si noti che le frequenze multiple dispari della fondamentale subiscono uno spostamento quando il raggio del secondo tratto di canna è molto grande. Ciò dimostra che esse sono associate a questo secondo tratto, mentre le frequenze multiple pari della fondamentale restano invariate durante tutta la trasformazione.

Nel secondo caso abbiamo un tratto lungo 50 cm e di raggio 2 cm congiunto con un tratto di pari lunghezza e raggio decrescente. Anche in questo caso si parte dalla risposta di un'unica canna aperta-aperta lunga 100 cm, e progressivamente ci si sposta verso il caso di una canna semi-aperta lunga 50 cm. Il secondo tubo infatti diviene sempre più simile ad un'ostruzione, e tende quindi ad assomigliare ad un'estremità chiusa. In questo caso spariscono le risonanze pari, e restano, correttamente, quelle multiple dispari della fondamentale, che rimane invariata.

Geometria	Risposta acustica	Risonanze
Restringiamo progressivamente il raggio del secondo tratto di tubo fino a renderlo capillare, cioè quasi indistinguibile da una vera e propria ostruzione del flusso acustico.	Le frequenze multiple dispari della fondamentale della canna intera restano invariate, mentre quelle multiple pari scompaiono progressivamente.	I massimi degli armonici multipli dispari della fondamentale scompaiono per un rapporto tra i diametri di 7 a 1

---