Che cos'è una membrana ideale

Una membrana ideale è l'esatto corrispondente bidimensionale di una corda ideale.

Essa, come la corda ideale, è caratterizzata da soli due parametri: la densità (in questo caso sarà la massa per unità di superficie ${\displaystyle \rho }$), e la tensione superficiale T (che ha dimensioni di una Forza per unità di lunghezza, cioè si misura in Nm^-1 nel sistema SI)

La membrana è ideale se

1. T è costante durante il moto della corda (cioè qualunque sia la sua deformazione)
2. T ha la stessa intensità lungo tutta la membrana, e, in ogni punto, agisce solo nella direzione tangente la membrana (cioè senza componenti perpendicolari alla superficie).
3. tutte le altre forze esterne (come la forza di gravità) sono trascurabili rispetto a T

Come si ricava l'equazione

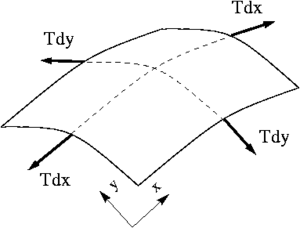
Il bilancio delle forze su un tratto infinitesimo della membrana di lati dx e dy si conduce in maniera del tutto analogo al caso della corda vibrante, perché si possono scomporre i contributi delle forze lungo l'asse x e y. In particolare si ha che La risultante delle forze che causa il moto è perpendicolare alla membrana, ed è la somma di due contributi (v. figura): quello ottenuto dal bilancio lungo l'asse x ${\displaystyle dF_{z}^{x}(x,y)=[T(x,y)+T(x+dx,y)]dy\approx Tdy{\frac {\partial ^{2}z}{\partial x^{2}}}dx\!}$, e quello ottenuto dal bilancio lungo l'asse y ${\displaystyle dF_{z}^{y}(x,y)=[T(x,y)+T(x+dx,y)]dx\approx Tdx{\frac {\partial ^{2}z}{\partial y^{2}}}dy\!}$.

• La somma dei due dà

${\displaystyle dF_{z}=dF_{z}^{x}+dF_{z}^{y}=Tdxdy\left({\frac {\partial ^{2}z}{\partial ^{2}x}}+{\frac {\partial ^{2}z}{\partial ^{2}y}}\right)}$

Questa forza va eguagliata al termine massa per accelerazione, che è pari a

${\displaystyle dm\cdot a=\rho dxdy{\frac {\partial ^{2}z}{\partial ^{2}t}}}$

• Si ottiene così la versione bidimensionale dell'equazione classica delle onde

${\displaystyle {\frac {\partial ^{2}z}{\partial x^{2}}}+{\frac {\partial z^{2}}{\partial y^{2}}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}z}{\partial t^{2}}}}$,

con

${\displaystyle c={\sqrt {\frac {T}{\rho }}}}$,

in totale analogia col caso della corda.

Membrana circolare

L'equazione che abbiamo scritto in coordinate cartesiane descrive tutte le onde in una membrana, qualunque sia la sua forma, ma è particolarmente adatta alle membrane di forma quadrata o rettangolare, perché tale è il reticolo formato dalle x e y.

In questo caso i modi normali si possono dedurre dai modi normali di una corda separatamente nelle direzioni x e y, e quindi la soluzione del moto sarà in generale una sovrapposizione di seni e coseni. I dettagli su quale combinazione dipendono ovviamente dalle condizioni al contorno e dalle condizioni iniziali del problema.

È però particolarmente importante il caso in cui la membrana ha forma di cerchio, perché questa è la forma in cui compare in molti strumenti musicali (tipicamente alcune percussioni quali i tamburi e i timpani).

Bencé l'equazione ricavata sopra si possa utilizzare, risulta particolarmente scomodo escprimere il cerchio in coordinate cartesiane, ed è più immediato passare alle coordinate polari mediante la trasformazione

${\displaystyle x=r\cos(\phi )\!}$,

${\displaystyle y=r\sin(\phi )\!}$.

Tralsaciando i dettagli, giungiamo direttamente alla forma che l'equazione d'onda assume in seguito a questo cambiamento di coordinate:

${\displaystyle {\frac {\partial ^{2}z}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial z}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}z}{\partial \phi ^{2}}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}z}{\partial t^{2}}}}$. (1)

Ora possiamo separare le variabili cercando una soluzione della forma

${\displaystyle z(r,\phi ,t)=R(r)\Phi (\phi )cos(\omega t)\!}$,

che, sostituita nell'equazione (1) la spezza in due equazioni separate, una per ${\displaystyle \Phi }$, ed una per R.

L'equazione per ${\displaystyle \Phi }$ è semplicemente quella del moto armonico

${\displaystyle {\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}+m^{2}\Phi =0}$.

Ciò significa che lungo ogni cerchio concentrico il profilo della membrana sarà sempre quello di un seno (o coseno).

L'equazione per R è un'equazione di tipo nuovo, più complicata, le cui soluzioni sono funzioni speciali (dette Funzioni di Bessel cilindriche), che determinano il profilo radiale della membrana del tamburo.

${\displaystyle {\frac {\partial ^{2}R}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial R}{\partial r}}+{\frac {m^{2}}{r^{2}}}R+n^{2}R=0}$.

Una visualizzazione di alcune di queste funzioni è riportata alla pagina Modi normali di una membrana circolare.

---