NOTA: tutti i campioni sonori delle percussioni sono stati eseguiti da Matteo Manzini il 04/12/2007. Ingegnere del suono: Valerio Carboni.

Struttura dello strumento

Rullante: membrana superiore	Rullante: membrana inferiore

Il rullante è un tamburo a cassa cilindrica. Il modello raffigurato è la versione a cassa corta del tamburo rullante militare, ed è usato come componente di una batteria. La cassa è metallica (ma in altri modelli può essere anche fatta di legno), ed ha un'altezza di circa 20 cm. La cassa è chiusa da entrambe le parti da membrane sintetiche aventi diametro di circa 35 cm. Si nota che nella parte inferiore è montata una cordiera. Essa consiste in un fascio di corde (in questo caso metalliche e ritorte), che possono essere poste a contatto della membrana, oppure allontanate da essa mediante la vite e i tiranti di regolazione visibili nella parte alta dell'immagine che ritrae della vista inferiore dello strumento. Le corde hanno una ben precisa funzione acustica che è illustrata nel prossimo paragrafo. A differenza di altri tamburi di dimensioni paragonabili, che possono venir percossi con le mani, il tamburo rullante viene percosso esclusivamente mediante bacchette di legno.

Caratteristiche acustiche

Acustica vuol dire innanzitutto geometria.

Osservando lo strumento possiamo farci un'idea di quali siano le parti che contribuiscono alla produzione del suono, e dei loro accoppiamenti. Esse sono:

1. La membrana superiore
2. la membrana inferiore
3. le corde (o "minugia")
4. la cassa

La membrana superiore e inferiore sono mutuamente accoppiate sia attraverso l'aria inclusa all'interno del tamburo, sia attraverso le vibrazioni dalla cassa. Le corde sono accoppiate sostanzialmente solo alla membrana inferiore, perché le vibrazioni della cassa sono sostanzialmente solo radiali.

Trascuriamo per il momento l'effetto della cassa, e concentriamoci sulle membrane. I modi di vibrazione di una singola membrana ideale sono descritti alla pagina modi normali di una membrana circolare, e sono anche illustrati nel caso del timpano. In quel caso abbiamo notato che l'effetto dell'aria inclusa nella grande caldaia vascolare è decisivo per la produzione di un suono di altezza definita.

Il caso del rullante è però molto diverso: la cassa è cilindrica, e l'aria inclusa non molta. L'effetto dell'aria è sufficiente ad accoppiare le membrane superiore ed inferiore, ma il suono che ne risulta è sempre di altezza indefinita. Il tamburo produce comunque un rumore a banda larga, ma piuttosto "rotondo", almeno finché non si usa la cordiera.

La membrana superiore viene eccitata direttamente dalla percussione, e quindi si muoverà secondo una sovrapposizione dei suoi modi normali. Dati raggio, densità e tensione della membrana possiamo calcolarne le frequenze, per confrontarle con quelle dell'intero strumento.

L'aria posta all'interno del tamburo è comprimibile, e quindi si comporta come una molla rispetto alle due membrane, che possono essere considerate a loro volta masse collegate a molle (anche le membrane hanno elasticità). Il modello fisico più semplice consiste allora nello studiare il tamburo come se si trattasse di due oscillatori accoppiati. Cominciamo con un "tamburo modello", assumendo che le due membrane abbiano uguale massa e tensione (anche se questo non è vero per i tamburi reali). Sappiamo dalla fisica come si comporta questo sistema (si veda la discussione sugli oscillatori accoppiati).

Se ogni oscillatore considerato isolatamente ha frequenza ${\displaystyle f_{0}}$, l'accoppiamento mediante una molla produce due frequenze distinte ${\displaystyle f_{1}}$ e ${\displaystyle f_{2}}$ tali che ${\displaystyle f_{1}<f_{0}<f_{2}}$. Nel rullante accade proprio così, ed anzi, non è difficile dimostrare che le due membrane vibrano nello stesso modo normale. le due frequenze corrispondono ad una differente fase tra di esse. In particolare: se le membrane oscillano in fase la frequenza sarà più bassa di quella della singola membrana isolata, mentre se oscillano controfase sarà più alta.

La ragione? Semplice, almeno per quanto riguarda i modi (0,1): basta ricordare la formula generale per "qualunque" oscillazione meccanica:

${\displaystyle f\propto {\sqrt {\frac {K}{m}}}}$,

dove K è l'elasticità del sistema, e m la sua massa.

• Nel primo caso (membrane in fase) la frequenza si abbassa perché l'aria compresa tra di esse si muove insieme alle membrane. Non conta la sua elasticità, ma la sua inerzia, che si va ad aggiungere a quella delle membrane. m aumenta, quindi, e f diminuisce.
• Nel modo in cui le membrane sono controfase, invece il baricentro dell'aria non si sposta, e quindi la partecipazione dell'aria si riduce al solo effetto molla, che si somma a quello delle membrane. Ora K aumenta, e, di conseguenza, anche f aumenta.

i primi modi normali delle membrane del rullante
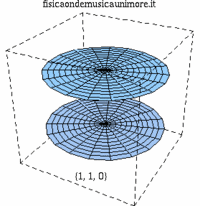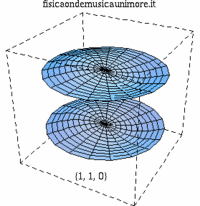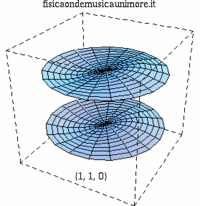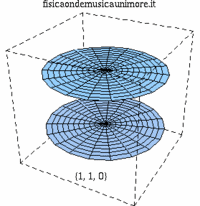
modo membrana singola	membrane in fase	membrane contro fase
{0,1}
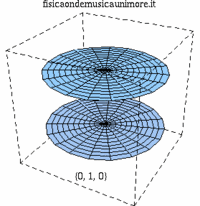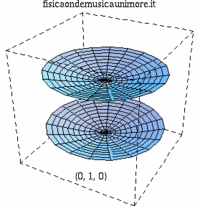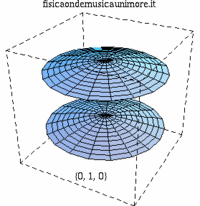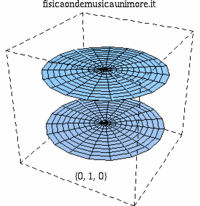
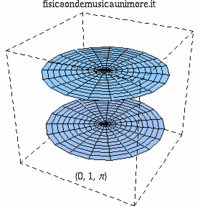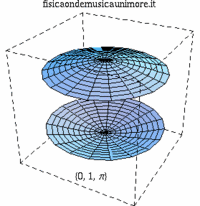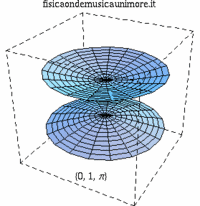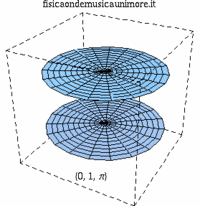
{1,1}

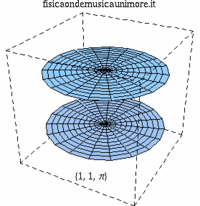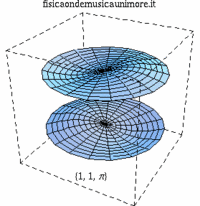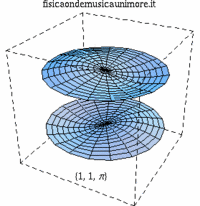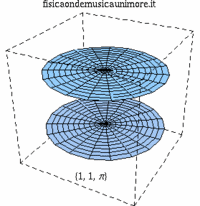
Nomen omen

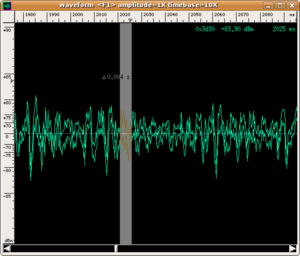
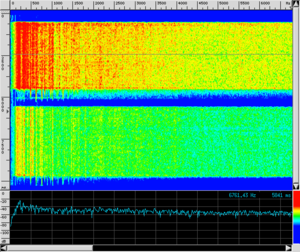
Il rullo del tamburo è ottenuto abbinando la tecnica del doppio colpo con le bacchette (uno col polso, uno con le dita) all'effetto delle corde, che vengono sollecitate a vibrare dalla membrana inferiore, e aggiungono il carattere secco e squillante alla successione di colpi, oltre che un rumore di fondo a tutta banda.

Dall'esame del tracciato si evidenzia che gli impulsi prodotti si susseguono alla distanza media di soli 4 centesimi di secondo l'uno dall'altro, equivalente ad una frequenza di ben 25 colpi al secondo. Anche riproducendo una porzione del campione a velocità dimezzata la successione resta molto fitta.

forma d'onda	sonogramma	Audio
PC_Rullo.mp3 Rullo, prima forte, poi piano	PC_Rullo_mezza_vel.mp3 Rullo piano, mezza velocità

Evidenza alle armoniche

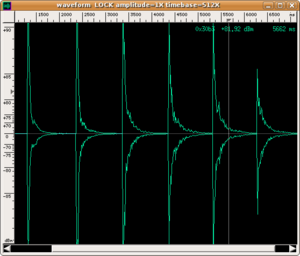
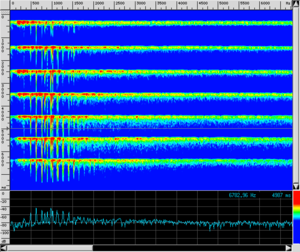
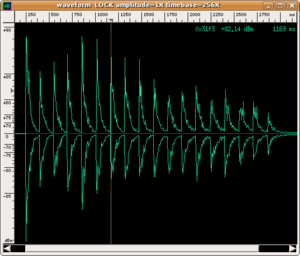
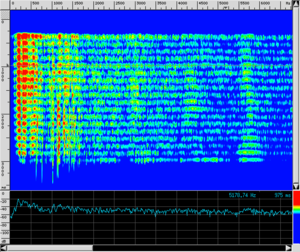
Lo spettro emesso dal rullante si estende su tutta la banda udibile, e, almeno nel breve tempo dell'impatto, esso non presenta picchi particolarmente evidenti. Per attribuire i picchi ai modi delle membrane serve un'analisi in alta risoluzione. Tuttavia restano abbastanza evidenti alcuni picchi durante il tempo (relativamente più lungo) della vibrazione libera. Nei nostri esempi essi sono da attribuirsi ai modi di vibrazione della cassa metallica dello strumento. Il suono prodotto dall'insieme di queste frequenze è piuttosto disarmonico, ma alcuni modi associati a queste frequenze decadono molto più rapidamente di altri, permettendo ad una nota o ad un'altra di affiorare dal mare sonoro.

L'esecutore può regolare il colore del suono (non l'intonazione, perché lo strumento resta ad altezza indefinita) percuotendo la membrana superiore in punti differenti. Nei seguenti esempi il punto di percussione viene spostato progressivamente verso il bordo, e il colore corrispondente si fa via via più chiaro.

forma d'onda	sonogramma	Audio
		PC_ArmoniciR.mp3 PC_ArmoniciR

forma d'onda	sonogramma	Audio
		PC_ArmoniciR2.mp3 PC_ArmoniciR2

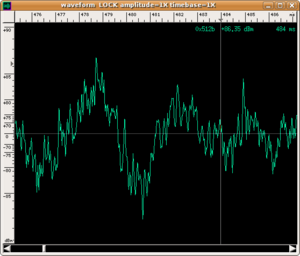
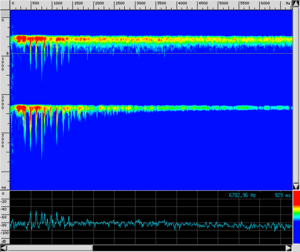
Il ruolo della cordiera

Come spiegato nel primo paragrafo, la cordiera può essere mossa tramite una vite, ed essere allontanata dalla membrana inferiore, fino a non esserne più in contatto anche durante le percussioni. Il suono dello strumento perde il colorito "metallico", e il suono diventa quello prodotto dalla sola risonanza del sistema formato dalle membrane, della cassa metallica, e dell'aria inclusa nello strumento.

forma d'onda	sonogramma	Audio
		PC_CordieraR.mp3 PC_CordieraR

Usi delle bacchette

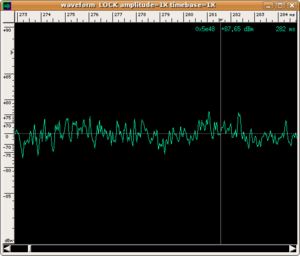
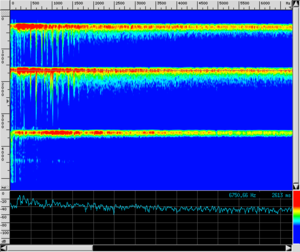
In questo esempio il suono dello strumento sul colpo singolo viene modificato percuotendo con la bacchetta prima solo la membrana, poi solo la costa metallica della cassa, e poi entrambe insieme.

forma d'onda	sonogramma	Audio
		PC_MezzoCostaPienoR.mp3 PC_MezzoCostaPienoR

---