type of boundary	"permitted" wavelengths
string with fixed ends (bore open at both ends)	${\displaystyle \lambda ={\frac {2L}{k}}}$ with ${\displaystyle k=1,2,\ldots }$
string with free ends (bore closed at both ends)	${\displaystyle \lambda ={\frac {2L}{k}}}$ with ${\displaystyle k=1,2,\ldots }$
string with one fixed end and one free end (bore closed only at one end)	${\displaystyle \lambda ={\frac {4L}{2k+1}}}$ with ${\displaystyle k=0,1,2,\ldots }$

• Actually, in the place of the physical length L of the bore, we need to insert into the previous formulae a effective length that considers the fact that the variation of impedance between the air inside and outside the tube varies gradually and not abruptly as happens at the fixed ends of strings.

We advise you to repeat the experiments with sound tubes in our virtual laboratory to more carefully observe:

• the phase inversion or non-inversion of a reflected pressure wave;
• the correction of effective length (which strongly depends on the presence of holes and the shape of the end of the bore);

The ability to select specific stationary waves in (open and closed) sound tubes is the basis for how all wind instruments and pipe organs function.

Let's calculate the distance of an obstacle through reflection

Many devices and even some animals use the wave reflection phenomenon to detect the presence of an obstacle. The localisation principle is very simple:

• sending a wave against an obstacle will generate a reflected wave
• by measuring the time elapsed between the instant of the generation of the wave and the instant of the arrival of the reflected wave, we can determine the distance of the obstacle. Given D is the distance of the obstacle and V is the wave speed in the medium, it is obvious that the elapsed time interval can easily be determined using the formula

${\displaystyle \Delta t={\frac {2D}{V_{\rm {wave}}}}}$

It is important to underline that this method will work if:

• the incident wavelength is much less than the transversal size of the obstacle
• the receiving apparatus is "ready" to discriminate between the two waves, the incident one and the reflected one, being received in rapid succession.

Echo and reverberation

In the case of sound waves, wavelengths vary from about 17 metres (for low-frequency sounds with very low pitch) to just a few millimetres (for high-frequency sounds with very high pitch). Moreover, due to physiological reasons, our ears are able to discriminate two sounds arriving in sequence but only if the separation time is about one tenth of a second. Considering that the speed of sound propagation in air is about 340 m/s, a quick calculation shows that, for human beings, this method is only effective for the localisation of very large objects located at distances greater than

${\displaystyle D={\frac {{V_{\rm {wave}}}\cdot \Delta t}{2}}={\frac {340\cdot 0.1}{2}}=17{\rm {m}}}$

In fact, with the previous formula, we have determined the conditions under which we can expect to experience the phenomenon of 'echo. An obstacle must be very large (for example, the side of a mountain) and located at least 17 metres from our ears!

Newton used the phenomenon of echo for the first ever attempt at determining the speed of sound. He made incredibly precise measurements (within 1% of the value known today) in the 65-metre long north cloister of Neville's Court at Trinity College, Cambridge, where he studied (see the photograph on the left). Observe that the time that Newton had to measure was less than a second (visit the page on the speed of sound, if you wish to know how Newton solved the problem).

In the case where there is no echo (i.e. the reflected sound reaches the observer in less than a tenth of a second after emission), there will be a reverberation, which is a more intense sound sensation caused by the fact that the reflected sound is superimposed to the sound from the source generating an impression of less distinctness and more difficult localisation of the sound source of the obstacle. Try to imagine, just like in a nightmare, screaming in a small, dark cave: the sound comes back to your ears confusedly and hinders even the minimum localisation of the walls. In this case, you would probably still perceive the echo phenomenon due to multiple reflections (even if the conditions for having an echo are not fulfilled, i.e. the walls are less than 17 metres from you). The reverberation phenomenon is of fundamental importance in the designing of concert halls. If you are interested in further study of these aspects, visit the page on architectural acoustics.

Technological applications of sound reflection

SONAR

The word SONAR, which has now become part of everyday vocabulary, is actually the acronym SO.N.A.R, which stands for SOund Navigation And Ranging. The name itself illustrates the fact that

• these devices exploit the reflection phenomenon of sound waves (consider that sound waves can propagate in water for kilometres at a speed of about 1,500 m/sec);
• they are used on vessels and submarines to detect the seabed or immersed bodies (such as schools of fish, other vessels, other submarines, etc.).

SONAR can be either passive or active. The former is used to identify the presence of sound sources, as they are simple 'ears' for listening to sounds that propagate underwater. The latter fully exploits the sound reflection phenomenon described previously. The units are built with devices for the transmission and reception of sound impulses (even ultrasonic) and with time of flight (or the 'back and forth' time) detectors of reflected sound waves. Obviously, being electronic devices, these detectors can have a time resolution between two successive sounds that is much lower than the limits of the physiology of the human auditory system and allows for the localisation of very close obstacles.

Nowadays, SONAR has been "emancipated" from its nautical origin and is employed in devices that use sensors and ultrasound:

• in mobile robots that must be able to move through an environment safely and autonomously. To do this, they are equipped with (along with other systems such as LASER and infrared scanners) ultrasound sensors (usually with a frequency of 40 kHz, well above the upper limit of audible frequencies, which is 20 kHz) that can localise any obstacles in the environment that could block their path. Any possible source of errors in the SONAR method of measuring distances can be due to:

a) an imprecise evaluation of the speed of sound propagation in the air (which depends, albeit weakly, on the temperature and humidity conditions of the air);

b) the nature of the object reflecting the sound wave (for example, if it is made of "phono-absorbent" material or has a rough surface that can cause the phenomenon of diffuse reflection) and its inclination with respect to the direction of propagation of the incident sound wave (which can compromise the sensitivity of the receiver at which only a minimal fraction of the reflected wave arrives). These errors, unless one is working in extreme environmental conditions, are more than acceptable over short distances. Proof of this can be seen in the existing sales of mobile robots that use ultrasound sensors to transport materials in large, sparsely decorated environments (such as infrequently-used long corridors in hospitals) or even as museum guides.

• remote controls for appliances with ultrasonic sensors;
• proximity switches (for example, on automatic gates);
• measuring systems for liquid levels in inaccessible cisterns or deep wells;
• devices mounted on car bumpers to assist with parking.

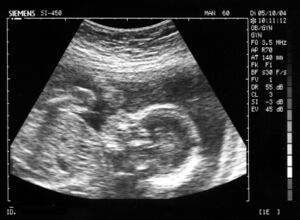
Ultrasonography

Sonograph of a 23-week-old foetus

Ultrasonography also uses the phenomenon of sound wave reflection. In this case, due to the small size of the details to be visualised through ultrasonography, ultrasounds with very small wavelengths (very high frequency) must be used. In fact, ultrasonography techniques use very high frequencies ranging from 1 to 10 MHz, which are generated by quartz crystals that can vibrate millions of times per second). The need to have a high resolution power (in other words, the ability see distinct objects that are very close), which is guaranteed by using high-frequency waves, is in direct contrast with the fact that these waves have less ability to penetrate body tissues (high-frequency waves are generally absorbed very quickly). Therefore, the choice of "range" of ultrasound frequencies must balance these two opposing needs. The ultrasonography technique is based on the various abilities of reflecting sound waves possessed by substances of different density and chemical composition. By moving the sonography probe at various angles across the areas to be studied and analysing the reflected waves, often per second, we can obtain information that has been translated into images and that can even be sequenced into films. The most widespread use of sonography allows us to see a foetus moving in its mother's uterus (see image on the right). A sonography examination is entirely operator-dependent because correct results depend on the ability of a properly trained operator to decode the sonographic images. One last comment: whoever has had a sonograph knows that, before being exposed to sound waves, the "skin" above the area to be studied is covered with a "gel": this substance acts as a impedance adaptor between the sonography probe and the internal organs. It modifies the skin's reflecting properties and its impedance to sound waves rendering it almost "transparent" to ultrasonic waves.

Echo-Doppler

An interesting "variant" of classic ultrasonography for use with blood vessels is the diagnostic test known as Echo-Doppler. Classic ultrasonography allows the study of the morphology of arterial and venous walls detecting:

• the presence of vessel stenoses (narrowings) due to lipid deposits (for example, the notorious cholesterol) or atherosclerotic plaques;
• the presence of thickenings and loss of wall elasticity.

Echo-Doppler

However, it cannot evaluate the hemodynamic repercussions (or actual blood flow) that these morphological anomalies have. To overcome this diagnostic limit, ultrasonography is used along with the Doppler technique allowing for the visualisation of moving parts (in this case, blood flow). This technique is based on the frequency shift of waves reflected by moving bodies. This shift depends on the speed of the reflecting body, and therefore, provides a "mapping" of the speed of blood flow at various points along the section of the vessel. The quantitative aspects of this frequency shift are well described on the page about the Doppler effect. In the image on the right, the "whitish" parts are the blood vessel and the red parts are the blood flow. Even more refined visualisation techniques also exists (used in Echo-colour Doppler sonography) that associate different colours with various velocities of blood flow.

In-depth study and links

• If you wish to learn about a simple device used to determine the quantisation conditions of open and closed bores, visit the page on the Kundt tube

• Obviously, the sound reflection phenomenon plays a fundamental role in determining the acoustic qualities of a closed environment. If you are interested in further study on this topic, visit the section on architectural acoustics.

• If you are interested in further study on the use of reflection to determine the speed of sound, visit this page.

• The reflection phenomenon effects every type of wave and is the basis of how mirrors (even in current language, we say reflecting mirror!) and, surprisingly, musical instruments function. Visit the page on reflection, where the topic is discussed more thoroughly.