Is it easy to make two sounds interfere?

As explained on the page about interference, the term "interference" refers to a superposition of waves that takes place in the following ways:

1. the superimposed waves are periodic waves having the same frequency (and sometimes amplitude);
2. the wave sources oscillate in phase, in other words perfectly synchronous or with a known "phase difference";
3. when we say constructive (or destructive) interference, we always refer to completely constructive (or destructive) interference;

Under these hypotheses, the phenomenon of interference occurs in such a way that a fixed a point in space will always be the site of either constructive or destructive interference at any time. The main problem of interference is determining, once the positions, oscillation frequencies and phases of all sources are known, if a given point in space is the site of constructive or destructive interference. However, if even one of the hypotheses is missing, interference is more complex and the waves superimpose without producing regularities that are easy to analyse quantitatively.

In the case of sound waves, it is very difficult to have sources with the properties described above and maintain the conditions of destructive or constructive interference long enough to carry out observations. This experimental difficulty was overcome by an observation by Herschel, who had the idea of making two waves coming from the same source interfere by causing them to superimpose after having forced them to follow two different pathways.

The Quincke tube: a device that demonstrates sound interference

Herschel's idea was developed by Quincke and perfected by König in a version that allowed for the creation of interference experiments with great ease. In the Quincke tube:

• A pure sound emitted by a tuning fork at a certain frequency enters a U-shaped tube and is distributed into the upper and lower branches of the U. One of the two branches is of variable length, i.e. the tube in question can be lengthened and shortened (similarly to the coulisse of a trombone). The two branches then merge in a single exit tube.

• If a microphone is placed at the exit, we can observe that, by varying the length of the movable branch, it detects a sound intensity with maxima and minima.

• What is happening? If we vary the difference in the pathways by moving the movable branch (the "coulisse"), this causes the sound waves in the two branches to gradually shift out of phase. When the difference in pathways is equal to a multiple of the wavelength, we can observe an increase of the exiting sound. This is known as constructive interference. If we continue to move the coulisse, we can create a difference in pathways that is equal to an uneven multiple of a semi-wavelength. This will cause the exiting sound to weaken until it disappears. This is known as destructive interference.

• Alternatively, the state of constructive and destructive interference can be observed by means of manometric capsules (invented by König) that can convert the variation of sound pressure of the air into a variation of the height of a flame placed at the exit of each individual tube and the common exit. When constructive interference occurs, we will see an increase of the flame amplitude at the common exit. When destructive interference occurs, the flame amplitude will diminish abruptly while the amplitude of the two flames at the exit of each individual tube will change alternately (this can be verified by a system of rotating mirrors that can magnify the amplitude vibration of the flame). This indicates that the two waves are out of phase by an uneven multiple of a semi-wavelength.

What can be measured with a Quincke tube?

Quincke's apparatus allows us, by measuring lengths and sound intensities, to indirectly determine:

• the wavelength of sound emitted by a tuning fork: this is obtained simply by measuring the length of the movable branch, which was added to shift from a condition of constructive interference (maximum sound intensity) to a condition of destructive interference (minimum sound intensity) and then multiplying the measurement obtained by two;

• the speed of sound in air: the frequency of the note emitted by the tuning fork is the same as the frequency of the pressure wave that propagates in the tube (observe that in the metal-air interface at the tuning-fork, what changes is the wavelength and not the frequency). By multiplying that frequency by the wavelength measured according to the above description, we will obtain an estimate of the speed of sound in air.

• the speed of sound in any gas: this is obtained simply by modifying the type of gas in the Quincke tube. It is interesting to observe that a simple device like the Quincke tube has allowed us to find the solution to an age-old experimental problem: how to measure of the speed of sound. With regards to this, see the page on the speed of sound, where you will find the ingenious method that Newton devised (about 200 years prior) to measure that very speed. Albeit, Newton's experimental apparatus was certainly more cumbersome: he used a cloister that was 65 m long!

Reflection interferometer: the Kundt tube

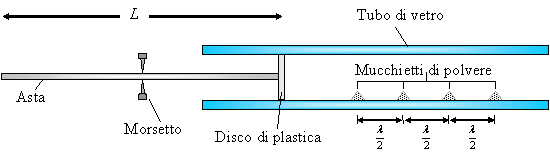
The idea behind the functioning of the Kundt tube is to exploit the phenomenon of sound reflection to cause interference between sound waves (generated by a vibrating plastic disc) and the waves reflected by the end of the tube (open or closed). The experimental apparatus is made of:

• a metal bar with a plastic disc of negligible mass attached at the end;
• a clamp fixed at the centre of the metal bar forcing a node in the oscillation of the bar;
• a glass tube in which the plastic disc can slide to modify the "effective length" of the tube;
• fine-grain powder spread inside the glass tube so that it will follow the variations of sound pressure inside the tube and be deposited in proximity to the oscillation nodes.

To recreate this experiment, you must take the following steps:

• firstly, rub the bar with a resin-soaked cloth to excite the longitudinal waves;
• when communicated to the light plastic disc, these oscillations make it act as a piston on the air in the tube generating a longitudinal sound wave (see illustration);
  
• the plastic disc is made to slide back and forth to find the position at which a stationary wave begins to appear in the tube: this can be seen when the fine powder begins to deposit at very precise, equidistant points (these are the nodes where oscillation is absent);
• by measuring the distance between two successive nodes, it is possible to find the wavelength of the stationary wave and verify that the conditions of quantisation described on the page about sound reflection are fulfilled.

The information regarding wavelength can be exploited in two ways:

• assuming that the speed of sound in air is known (measured by another way), it is obviously possible to find the frequency of the stationary wave and, therefore, the longitudinal oscillation frequency of the bar, which is obviously the same (remember that the frequency does not change at the plastic disc-air interface!). Recalling that the fundamental oscillation frequency f₀ of a longitudinal bar of length L and density ρ is

${\displaystyle f_{0}={\frac {1}{2L}}{\sqrt {\frac {Y}{\rho }}}}$

knowing f₀ can be used to estimate Young's modulus of the material from which the bar is made.

• assuming instead that the frequency of the bar is known (and, therefore, the longitudinal oscillations of air) it is possible to find the speed of sound again.

A double Kundt tube

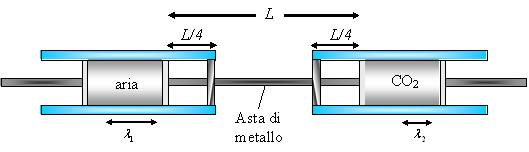
The Kundt tube can be modified to measure another important parameter for the determination of the speed of sound: the adiabatic index γ, which is the ratio of the heat capacity at constant pressure and heat capacity at constant volume of various gases. The experimental apparatus should be modified in the following way:

• two Kundt tubes are interfaced to create two cavities containing different gases (for example air and Carbon Dioxide ${\displaystyle CO_{2}}$;
• the tubes are connected by a bar in which longitudinal elastic waves are excited and the bar is fixed at the ends of the tubes and at a distance L/4 from the bar ends. These constraints make the bar vibrate in its second longitudinal mode of vibration;
• the bar communicates its oscillations to the gases in the cavities through a plastic disc;
• the length of the cavities is varied by sliding the two lateral tubes until the formation of piles of powder indicate the creation of a stationary wave.

Measuring the distance between the piles of powder (nodes), we can determine the wavelength in both air and Carbon Dioxide. As the frequency of the stationary waves in both cavities is the same (they have been excited by the same bar!) we can write

${\displaystyle {\frac {\lambda _{CO_{2}}}{\lambda _{aria}}}={\frac {v_{CO_{2}}}{v_{aria}}}}$

from which, recalling that (see the page on speed of mechanical waves), the speed of sound in a gas is given by

${\displaystyle v={\sqrt {\frac {\gamma P}{\rho }}},}$

and that the pressure of the two gases (that of the atmosphere not the one due to the sound wave!) can be considered identical, we can write

${\displaystyle {\frac {\lambda _{CO_{2}}}{\lambda _{air}}}={\frac {v_{CO_{2}}}{v_{air}}}={\sqrt {{\frac {\gamma _{CO_{2}}}{\gamma _{air}}}\cdot {\frac {\rho _{air}}{\rho _{CO_{2}}}}}}}$

Kundt^[1] measured the ratio

:${\displaystyle {\frac {\lambda _{CO_{2}}}{\lambda _{air}}}=0.780}$. 

Knowing that

${\displaystyle {\frac {\rho _{CO_{2}}}{\rho _{air}}}=1.53}$

and

${\displaystyle \gamma _{air}=1.403,\,}$

he was able to measure the adiabatic coefficient for carbon dioxide finding:

${\displaystyle \gamma _{CO_{2}}=\left({\frac {\lambda _{CO_{2}}}{\lambda _{air}}}\right)^{2}\cdot \gamma _{air}\cdot {\frac {\rho _{CO_{2}}}{\rho _{air}}}\simeq 1.31}$

In-depth study and links

For further study on interference and more quantitative demonstrations, see the following pages

• Antennae and interference, in which is explained how to exploit the interference phenomenon to design devices (antennae) that can transmit and receive waves in very precise directions;
• Mathematical aspects of interference, in which the conditions of constructive and destructive interference are derived;
• Interference between reflected waves and sound reflection, in which are illustrated how waves are reflected at the end of an open or closed sound tube;
• Harmonic wave interference, in which interference of particular waves is examined.
• Speed of sound, in which the importance of the adiabatic coefficient in determining the speed of sound in gases is illustrated.

Furthermore, you can experiment directly with the interference phenomenon using the 2D wave interactive applet or by following one of the guides to using applets.

---

---