Un caso di studio: la vocale "A"

Nella pagina Semplici modelli per la voce abbiamo dimostrato che la conoscenza della posizione dei primi due picchi (detti formanti) nella risposta in frequenza del tratto vocale è sufficiente per determinare la vocale pronunciata, e distinguerla dalle altre. In particolare abbiamo utilizzato una simulazione numerica per calcolare la posizione delle formanti a partire dalle misure della sezione del tratto vocale.

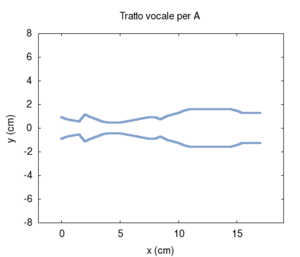
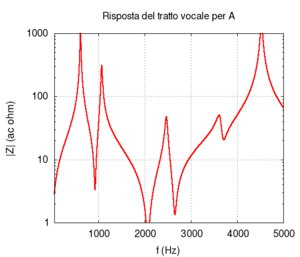
disegno (solo indicativo)	misure radiografiche	risposta in frequenza

Ora concentriamoci sulla sola vocale A, e vediamo se possiamo ottenere una comprensione più concreta della forma del suo spettro, e se riusciamo a collegarla alla caratteristica geometrica più evidente del tratto vocale, cioè la concatenazione di un tratto più stretto seguito da uno più largo.

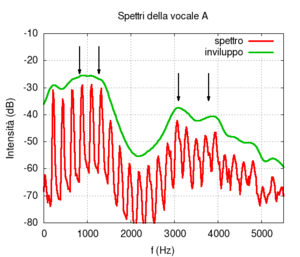
Se osserviamo lo spettro del suono A vediamo che esso si compone di una sequenza di picchi stretti in rapporto armonico (in rosso nella figura a lato), modulati da una forma più dolce con picchi meno pronunciati e più distanziati tra loro (evidenziata in verde). La presenza dei picchi in rosso è dovuta all'azione della glottide, che produce un'onda pressoché triangolare formata da una successione armonica di componenti. Ovviamente questa struttura non dipende dalla vocale pronunciata, ma cambia, ad esempio, al variare della particolare nota che viene intonata (anche nel parlato le vocali hanno una "nota" di riferimento). È la struttura in verde su cui dobbiamo concentrarci, perché quella non dipende dall'azione della glottide, ma dall'effetto filtro del tratto vocale. La curva in verde, i cui picchi più prominenti sono evidenziati dalle frecce, è la firma distintiva di ciascuna vocale.

Possiamo vedere che la "firma" della A consiste in due picchi piuttosto ravvicinati intorno a circa 1000 Hz, seguiti da una vasta zona antirisonante (cioè priva di picchi) fino a circa 3000 Hz. Entrambe queste caratteristiche sono ben evidenti nel disegno.

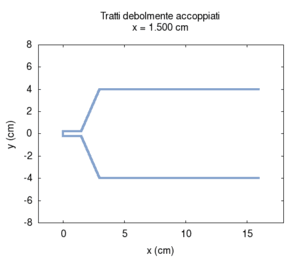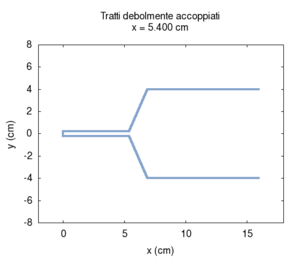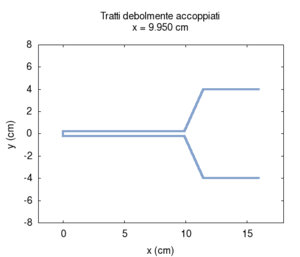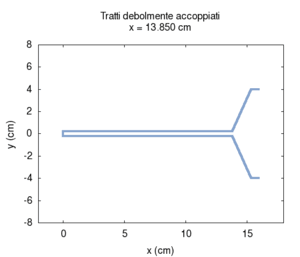
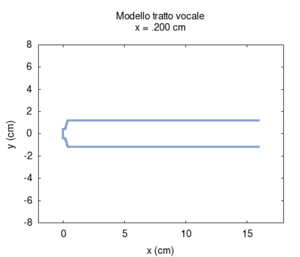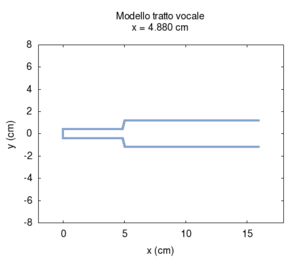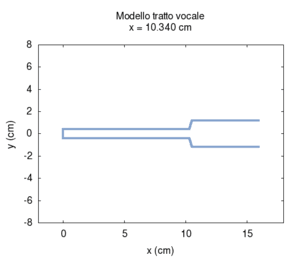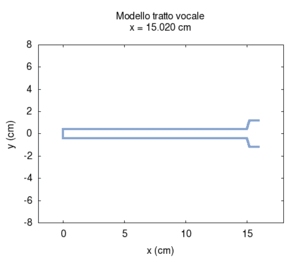
Ora torniamo al nostro modello, ma, questa volta, semplifichiamolo ulteriormente per capirlo meglio. Rifacciamo la simulazione assumendo che i due tratti di tubo siano cilindrici. Trascuriamo anche il fatto che parte del suono viene irradiato dalla bocca. Per avere una visione migliore eseguiamo tante simulazioni facendo variare la lunghezza relativa dei due tratti (si veda l'animazione qui sotto). Le risonanze ad ogni posizione cambiano in modo sistematico (animazione nel mezzo). Se le rappresentiamo in funzione della posizione del punto di congiunzione tra i due tubi, otteniamo uno schema simmetrico (figura più a destra). Si tratta ora di interpretarlo.

Geometria	Risposta acustica	Risonanze

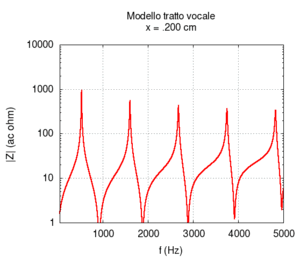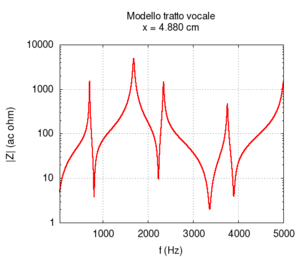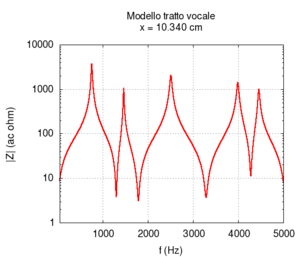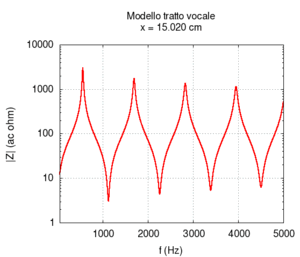
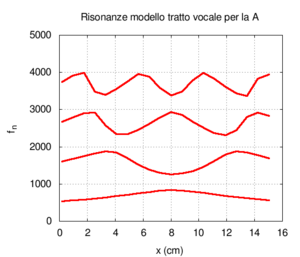
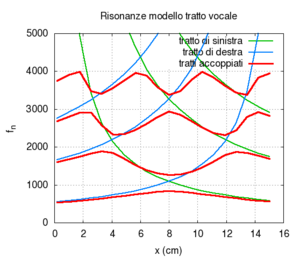
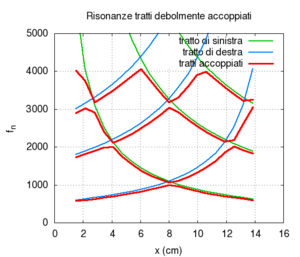
Lo schema si interpreta facilmente se vi sovrapponiamo le frequenze proprie dei due tratti di tubo calcolate come se essi fossero scollegati l'uno dall'altro.

Infatti, se seguiamo il percorso dell'onda sonora dalla glottide nel tratto di tubo stretto verso la bocca, vediamo che le condizioni di propagazione subiscono un cambiamento improvviso nel punto in cui il tubo si allarga. L'onda viene in parte riflessa indietro verso la glottide, e in parte propagata nel tratto di tubo più largo. Si ha così un fenomeno di rifrazione in una dimensione, che modifica le proprietà dell'onda trasmessa. Per un'illustrazione estesa del fenomeno si vedano le pagine rifrazione nelle corde e rifrazione nelle canne.

Si nota che le frequenze risultanti dell'intero tubo sono ben sovrapponibili alle frequenze dei singoli tubi disaccoppiati finché si rimane vicino dagli incroci. Per esempio x tra 0 e 5 cm la frequenza fondamentale del sistema coincide sostanzialmente con la frequenza del solo tratto di destra, in quanto la fondamentale del tratto di sinistra è molto più acuta. Per x maggiore di 11 cm la situazione è capovolta, e la fondamentale corrisponde sostanzialmente da una risonanza del solo tratto di sinistra.

Quando le frequenze dei due tratti disaccoppiati sono identiche si ha un incrocio tra le curve azzurre e verdi. Ad esempio per ${\displaystyle x=8}$ il tratto di destra e quello di sinistra hanno la stessa lunghezza, e quindi la stessa fondamentale (e le stesse armoniche). Tuttavia proprio in questi punti la curva rossa si discosta dalle curve azzurra e verde.

Il motivo sta nell'accoppiamento tra i due tratti, che gioca un ruolo tanto più importante quanto più influente diventa l'interferenza tra l'onda riflessa nel tratto stretto e quella trasmessa nel tratto largo.

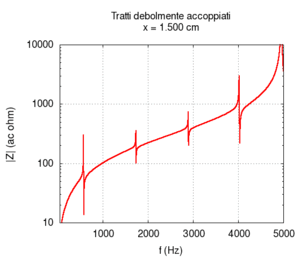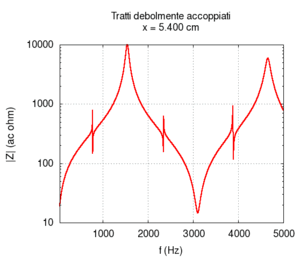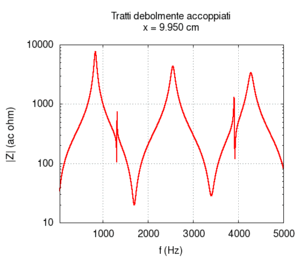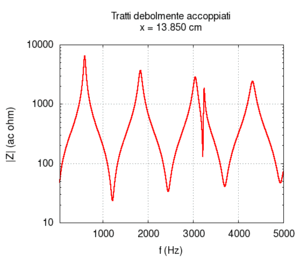
È oltre lo scopo di questa pagina dimostrare analiticamente che la distanza tra le frequenze effettive è tanto maggiore quanto più accoppiati sono i tubi, ma possiamo fare una rapida verifica numerica: se esageriamo la differenza tra i raggi dei tubi, il loro accoppiamento diminuisce, e quindi la risposta complessiva deve assomigliare maggiormente a quella di due tubi indipendenti. In altre parole, se i diametri dei due tubi sono molto differenti, le frequenze in rosso si avvicineranno ai punti di incrocio.

Per disaccoppiare i due tratti, pur lasciandoli comunicanti infatti è sufficiente mal adattare le loro impedenze (si veda Adattamento di impedenza), e, questo, da un punto di vista acustico, significa semplicemente rendere la sezione di uno molto più grande della sezione dell'altro. Questa configurazione, ovviamente, non coincide con nessun tratto vocale reale, ma ci serve semplicemente come controllo.

Osservando il risultato del calcolo vediamo chiaramente che la curva grossa in rosso, corrispondente al tratto completo si avvicina maggiormente alle curve in verde e azzurro, corrispondenti ai due tubi separati, e, in particolare, che le frequenze si avvicinano tra loro ai punti di incrocio.

Geometria	Risposta acustica	Risonanze
Un caso limite del tratto modello. Rendendo la sezione del primo tratto molto più piccola di quella del secondo tratto (cioè disadattando le impedenze acustiche) la risposta deve assomigliare maggiormente a quella dei due tratti trattati come tubi separati.	L'impedenza di uno dei due tratti di tubo è ora molto maggiore di quella dell'altro, e infatti appaiono dei picchi molto piccoli sovraimposti ad un profilo decisamente più grande.	In effetti si vede che la risposta del tratto completo si avvicina alle risposte dei due tratti, e, in particolare, le frequenze ci avvicinano nei punti di incrocio.

---