Un paio di esempi

1. Le irregolarità del terreno trasmettono ad ogni autoveicolo delle forze che potrebbero sgangherarne le parti, per non parlare del disagio dei viaggiatori. Tutti hanno visto (almeno in qualche film western) gli assi e le ruote di una carrozza a cavalli lanciata a velocità disintegrarsi per colpa di una buca o di un sasso. Se questo non accade in continuazione anche alle nostre vetture è per merito delle sospensioni, che altro non sono che sistemi oscillanti fortemente dissipativi, in grado di assorbire le sollecitazioni, e disperderne l'energia sotto forma di calore.
2. Tutti sanno che in una lavatrice (specie nei modelli un po' datati) la centrifuga non produce oscillazioni quando la macchina è a pieno carico, mentre se il bucato è più piccolo i panni tendono ad accumularsi da una parte, producendo scossoni e colpi ritmici.

Cosa hanno a che fare questi fenomeni con la risonanza?

Vibrazioni e risonanza

I motori, come tutte le macchine meccaniche, contengono parti rotanti con velocità precise, cioè con precise frequenze di rotazione. In molti casi è possibile dire a che velocità un motore sta girando semplicemente ascoltando il suono che produce (provate con la lavatrice, e non dimenticate il 2π). Tutti sappiamo che più acuto è il suono, maggiore è la velocità di rotazione, e questo collegamento si usa, a volte, magari inconsapevolmente, per cambiare marcia mentre si guida.

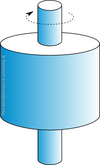
• Il caso che ci interessa come modello è quello di un albero su cui è innestato un cilindro (potrebbe essere il cestello della lavatrice, ma anche il sistema di ingranaggi dell'albero di un motore).

• Consideriamo dapprima il sistema rotante libero (come accade nella lavatrice). Nel caso ideale il cilindro ha massa perfettamente omogenea, cioè equamente distribuita. Esso quindi possiede un momento angolare costante e parallelo all'asse dell'ingranaggio, e le forze che l'ingranaggio esercita sull'albero sono perfettamente bilanciate. Ad ogni punto del disco corrisponde un punto diametralmente opposto, e le due forze centrifughe che si esercitano sull'albero da parte di questi punti corrispondono ad una trazione nel piano dell'ingranaggio. Le forze agenti sull'albero hanno risultante nulla nel piano, e quindi il cilindro ruota senza sforzo sull'asse.

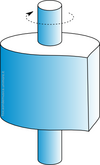
• Se però aggiungiamo una piccola imperfezione, o una massa extra da una sola parte del disco (il piccolo bucato), la musica cambia... anzi comincia. La forza esercitata dalla massa extra sull'albero non è più bilanciata da quella di una massa uguale posta simmetricamente rispetto all'asse. L'asse viene "tirato" nella direzione della massa squilibrante da una forza di intensità proporzionale al quadrato della velocità angolare con cui la massa ruota e alla sua distanza dall'asse (forza centrifuga).

Nella lavatrice il motore è soggetto a questa forza oscillante solo durante il tempo della centrifuga, e quindi non è particolarmente dannoso, ma uno sbilanciamento strutturale (cioè sempre presente) in un motore che ruota ad alta velocità può provocare il grippaggio o la rottura del meccanismo. La costruzione deve essere quindi accurata, e gli attriti interni devono essere opportunamente ridotti per mezzo dei lubrificanti. Qui però non ci interessa studiare l'usura del sistema, ma la sua vibrazione.

Isolamento dalle vibrazioni

Posto che gli ingegneri lavorano sodo per costruire le parti del motore di una Ferrari nel modo migliore, in una lavatrice non possiamo evitare che il carico sia sbilanciato. Lo stesso vale per tutte le macchine in cui gli ingranaggi non sono liberi, ma sono sottoposti a complessi sistemi di forze provenienti dagli altri meccanismi, dai vincoli e dai carichi esterni. In poche parole: non importa quanto sofisticati siano, tutti i sistemi meccanici sono soggetti a vibrazioni.

Studiando il fenomeno della risonanza possiamo però cercare di isolare le vibrazioni, in modo che esse si trasmettano all'esterno nella minor misura possibile.

In una lavatrice, o in un'automobile, l'isolamento è ottenuto per mezzo di un opportuno sistema di molle e dissipatori che "sospendono" il cestello in modo che parte dell'energia che lo mette in oscillazione sia trasformata in energia potenziale delle molle, e poi dissipata negli attriti interni.

L'isolamento del sistema più in generale richiede i seguenti passi:

1. studio dei modi normali del sistema, che ce ne rivela le frequenze proprie, cioè le frequenze alle quali il sistema può entrare in risonanza
2. studio della risposta in frequenza del sistema, che ci permette di evidenziare quali siano le frequenze maggiormente responsabili delle vibrazioni dannose o fastidiose
3. studio delle risonanze, per determinare esattamente quali debbano essere le caratteristiche del sistema di sospensione che garantisce l'isolamento desiderato.

Nei sistemi reali tutto questo processo può essere molto complesso, e prevede sia misurazioni sperimentali, sia complessi calcoli, ma nei sistemi più semplici possiamo risolvere tutto con carta e matita. Eccone un esempio.

Il nostro primo isolamento

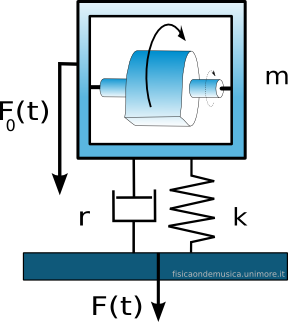
Mettiamo alla prova ciò che sappiamo sulla risonanza, e cerchiamo un modo per isolare il sistema oscillante più semplice. Possiamo immaginare proprio il caso della lavatrice, un po' semplificato, inserendo il motore asimmetrico in un supporto, e montando il tutto su una sospensione elastica con attrito.

Supponiamo che il sistema abbia un solo grado di libertà, cioè che possa muoversi solo sulla verticale. In altre parole modellizziamo il sistema come un oscillatore armonico semplice. La teoria di questo sistema è esposta nel dettaglio nella pagina sul moto armonico e sull'impedenza dell'oscillatore armonico. Qui ci interessa solo ricordare il fatto che l'oscillatore è caratterizzato da una sola frequenza di risonanza prossima a

${\displaystyle 2\pi f_{0}={\sqrt {\frac {k}{m}}}}$

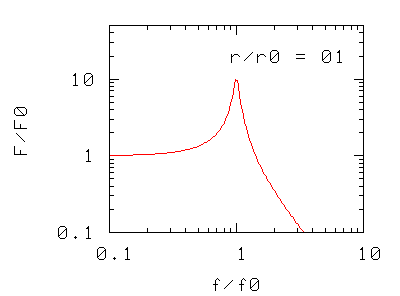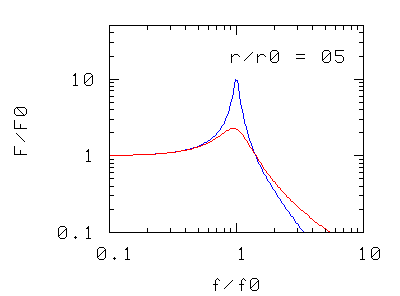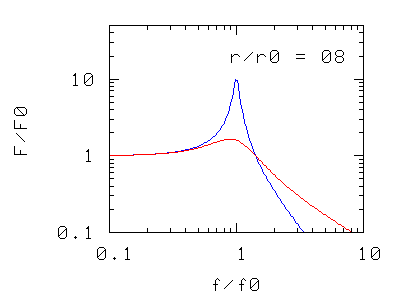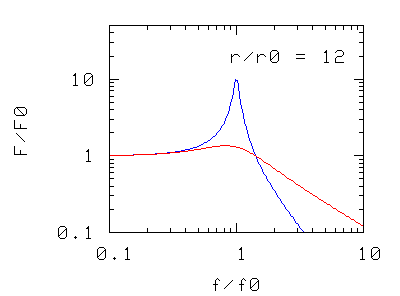
e che questa frequenza indica il punto "debole" del sistema. Una forza esterna oscillante anch'essa alla frequenza f₀, anche se di piccola intensità, è in grado di far compiere grandi oscillazioni al sistema (si veda il grafico della risonanza dell'oscillatore singolo).

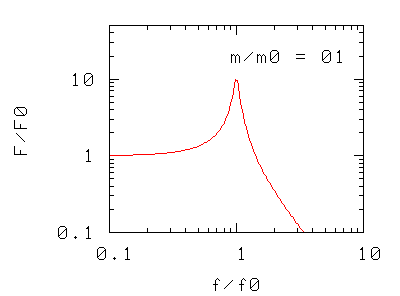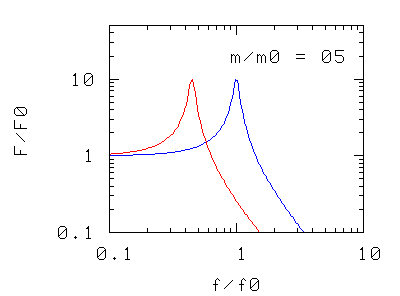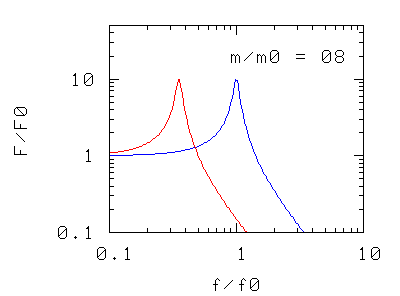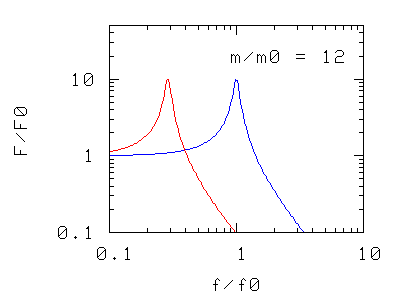
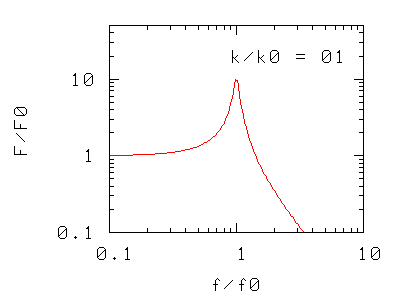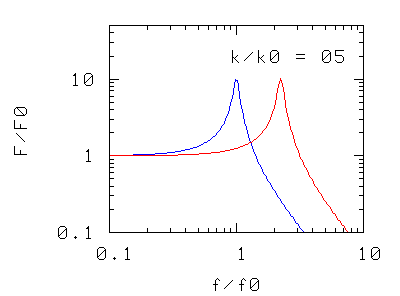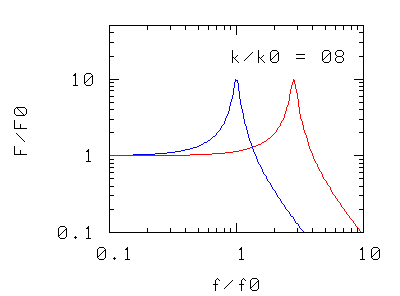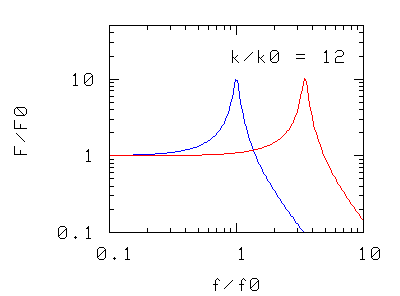
Abbiamo solo tre modi di intervenire sulla risonanza: cambiare la massa, cambiare la costante elastica (p.es. aggiungendo altre molle in serie o in parallelo), o cambiare il coefficiente d'attrito. I grafici rappresentano, nei tre casi, la forza massima F che l'oscillatore trasmette al basamento quando l'oscillatore è sottoposto ad una forza di ampiezza massima ${\displaystyle F_{0}}$ e di frequenza f.

massa variabile	molla variabile

Nei due casi precedenti si osserva che la frequenza di risonanza del sistema si sposta

• verso valori più piccoli aumentando la massa oscillante,
• verso valori più alti aumentando la costante elastica, cioè la rigidità della molla di sospensione (in pratica aggiungendo più molle in parallelo)

La forma della curva di risonanza, a parte la traslazione "rigida" non è modificata.

attrito variabile

Le diverse curve del grafico rappresentano il comportamento del sistema per valori crescenti del coefficiente d'attrito. Osserviamo che la risposta del sistema, cioè l'ampiezza della sua oscillazione viene fortemente smorzata in corrispondenza della frequenza di risonanza del sistema rimane invariata per qualunque valore dello smorzamento in corrispondenza della frequenza ${\displaystyle {\sqrt {2}}f_{0}}$ aumenta leggermente per frequenze superiori a ${\displaystyle {\sqrt {2}}f_{0}}$

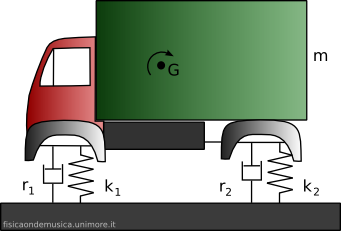
Ne abbiamo dedotto tre modi elementari di isolare il sistema, nota la sua frequenza di risonanza. Ovviamente il calcolo è meno semplice per sistemi che possono oscillare in più modi differenti (sistemi con più gradi di libertà), ma si basa sugli stessi principi. Lo schema del motocarro qui a fianco, ad esempio, pur essendo ancora lontano dalla complessità di un veicolo reale, possiede due gradi di libertà perché, oltre al moto verticale del suo baricentro g, esso può ruotare attorno al baricentro, sempre rimanendo nel piano del disegno. Aggiustando i parametri k₁, r₁, k₂ ed r₂, noti la massa m e il momento di inerzia baricentrale del veicolo, si possono smorzare le oscillazioni che potrebbero compromettere la stabilità dell'assetto di marcia.

Collegamenti

• Per il collegamento tra la rotazione, il moto armonico, le oscillazioni si veda la pagina sul moto armonico).
• Le funzioni di risposta sono descritte in impedenza, e nei vari casi particolari, in impedenza meccanica, impedenza elettrica, impedenza acustica

---