"Uno strano accordo"

Uno dei maggiori problemi tecnologici ancora irrisolti nell'anno 1665 consisteva nello sviluppare un sistema per determinare in modo accurato la longitudine su una nave in navigazione.

Questo problema si risolve costruendo un orologio in grado di misurare il tempo con sufficiente precisione nonostante i movimenti della nave. Uno degli orologi più precisi allora disponibili era l'orologio a pendolo, inventato da Christiaan Huygens pochi anni prima, nel 1657. Huygens si trovava appunto in navigazione per conto della Royal Society, e stava studiando il comportamento degli orologi a pendolo in quelle condizioni, quando si accorse di una strana coincidenza.

Costretto in cabina da una malattia, ebbe modo di osservare a lungo una coppia di orologi a pendolo, e in una lettera del 27 febbraio^[2] disse di aver

"percepito uno strano tipo di accordo in questi orologi sospesi uno accanto all'altro".

In sostanza, pur partendo da condizioni iniziali casuali, gli orologi, dopo un certo periodo di tempo, si trovavano sempre ad oscillare in controfase. Huygens notò anche che il fenomeno non si verificava se gli orologi erano posti distanti l'uno dall'altro, oppure se erano fatti oscillare in piani perpendicolari. Presto concluse che il fenomeno era dovuto all'accoppiamento tra i pendoli dovuto agli impercettibili movimenti della base comune su cui essi erano montati. Egli cercò anche di formulare una teoria più quantitativa del fenomeno, ma i tempi non erano maturi per questo (Newton pubblicò i suoi Principia solo vent'anni più tardi).

Anche in virtù di queste osservazioni, si capì ben presto che l'orologio a pendolo non poteva essere utilizzato per risolvere il problema della determinazione della longitudine, in quanto troppo sensibile ai movimenti della nave, e ad altri ancor più sottili, come quelli che provocano lo "strano accordo" .

Tuttavia il fenomeno della sincronizzazione, per la prima volta osservato da Huygens in un contesto meccanico, si è rivelato un fenomeno importante e comune a molte diverse classi di sistemi.

La caratteristica comune a tutti questi sistemi, che è responsabile dell'emergenza di fenomeni di auto-organizzazione e sincronizzazione è che la loro dinamica è di tipo non lineare.

Sincronizzazione di metronomi

È possibile realizzare una versione divertente dell'osservazione di Huygens utilizzando alcuni metronomi, come illustrato nel filmato. In questo caso, a differenza di quanto accadeva per i pendoli di Huygens, la sincronizzazione avviene in fase, anziché controfase (ed avviene in un tempo molto più breve), ma il fenomeno conserva la sua magia. ^[3]

Prima di entrare nei dettagli vediamo le caratteristiche generali del fenomeno, usando le utili Figure di Lissajous per l'analisi del caso più semplice: quello in cui ci sono solo due pendoli.

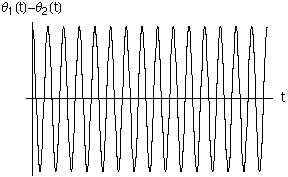
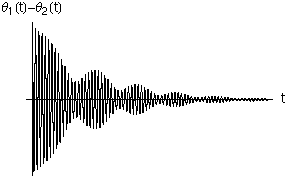
• Nella colonna di sinistra sono riportati gli sfasamenti relativi dei due metronomi. Si nota che, mentre nel caso lineare gli sfasamenti continuano ad oscillare, indicando la presenza di battimenti, nel caso non lineare la differenza di fase diminuisce progressivamente, fino a 0. Quando la differenza di fase è zero i metronomi sono "sincronizzati", e oscillano "all'unisono".
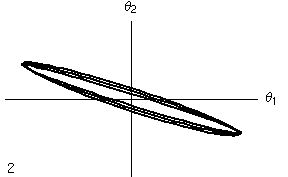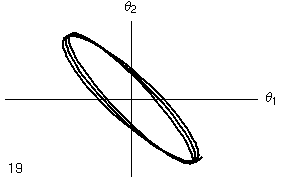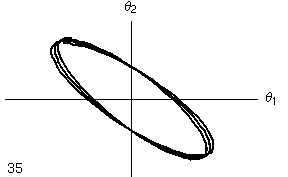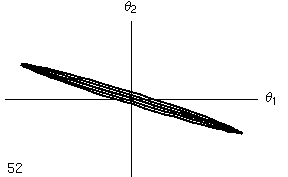
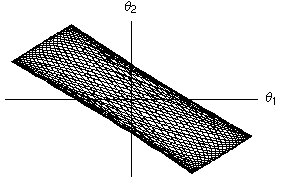
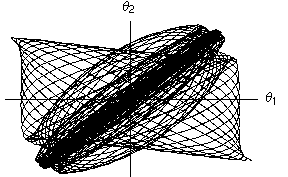
• Nelle due colonne seguenti l'angolo di oscillazione di un metronomo è tracciato in funzione dell'angolo di oscillazione dell'altro metronomo. Si tratta dello stesso diagramma, ma nella versione animata si mostra l'evoluzione temporale dell'oscillazione (l numero indica il numero di periodi di oscillazione di ciascun metronomo), mentre nell'ultima colonna si mostra l'evoluzione per tutto il tempo che si è simulato, pari a circa 50 periodi.
• Mentre nel caso lineare si nota che il moto continua ad oscillare nell'ambito del quadrilatero limite, nel caso non lineare si nota che, dopo un transiente iniziale, le oscillazioni si concentrano lungo la diagonale del I e III quadrante, di nuovo indicando un'oscillazione in fase (per l'interpretazione di questi diagrammi si veda la pagina dedicata alle Figure di Lissajous) .

	Differenza di fase	Figura di Lissajous (animazione)	Figura di Lissajous
Lineare
Non lineare

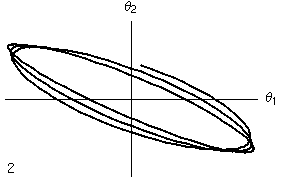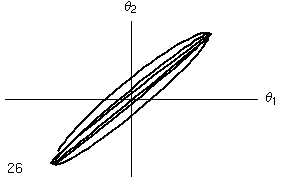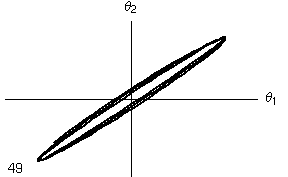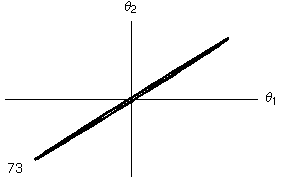
Approfondimenti

• Il pendolo semplice non è di per sé un oscillatore lineare. Infatti nella sua equazione del moto compare la funzione seno, il che significa che il pendolo approssima un oscillatore lineare solo per piccole oscillazioni (si veda la pagina sugli effetti non lineari).

Oscillatore armonico ideale (lineare)	${\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\theta =0}$
Pendolo senza attrito	${\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\sin(\theta )=0}$

• I metronomi (come pure gli orologi a pendolo) non sono nemmeno pendoli semplici. Infatti questi dispositivi contengono un ingegnoso meccanismo, detto scappamento, che consente alla molla che li alimenta, di liberare la sua energia poco a poco, attraverso una serie di piccoli impulsi. La molla cioè scarica dei "colpetti" sul pendolo, solo quando questo si trova ad oltrepassare, nella sua oscillazione, un certo angolo. In questo modo l'energia fornita dalla molla compensa la perdita di energia dovuta agli attriti, e l'oscillazione può essere mantenuta in moto finché la molla non sia del tutto scarica. Le oscillazioni sono libere tra un "colpetto" e l'altro, e si mantengono isocrone. Un rudimentale modello per questo congegno consiste nell'aggiungere un termine diattrito, e un termine non lineare detto "di Van der Pol" che rappresenta l'azione dello scappamento

Modello di metronomo (pendolo con scappamento)	${\displaystyle {\ddot {\theta }}+\omega _{0}^{2}\sin(\theta )+\omega _{0}\mu \left[\left({\frac {\theta }{\theta _{0}}}\right)^{2}-1\right]{\dot {\theta }}=0}$

• Quando diversi metronomi vengono posti su una base comune, libera anch'essa di muoversi, come l'assicella che rotola su lattine del filmato, gli impulsi rilasciati da ciascuno scappamento trasferiscono momento non solo al "proprio" pendolo, ma anche agli altri, attraverso la base. Equivalentemente possiamo dire che i metronomi ora sentono una forza apparente dovuta al moto della base, in quanto si trovano ad oscillare in un sistema non inerziale. Un altro termine si deve aggiungere all'equazione, e quindi, nel caso di due metronomi abbiamo il sistema

Due metronomi su base mobile

${\displaystyle {\begin{cases}{\ddot {\theta }}_{1}+\omega _{0}^{2}\sin(\theta _{1})+\omega _{0}\mu \left[\left({\frac {\theta _{1}}{\theta _{0}}}\right)^{2}-1\right]{\dot {\theta }}_{1}-\beta \cos(\theta _{1}){\frac {d^{2}}{dt^{2}}}[\sin(\theta _{1})+\sin(\theta _{2})]=0&\\{\ddot {\theta }}_{2}+\omega _{0}^{2}\sin(\theta _{2})+\omega _{0}\mu \left[\left({\frac {\theta _{2}}{\theta _{0}}}\right)^{2}-1\right]{\dot {\theta }}_{2}-\beta \cos(\theta _{2}){\frac {d^{2}}{dt^{2}}}[\sin(\theta _{1})+\sin(\theta _{2})]=0\end{cases}}}$

dove si è detto

${\displaystyle \omega _{0}^{2}={\frac {g}{L_{eff}}}}$

la frequenza propria di ciascun pendolo, se fosse un oscillatore armonico

${\displaystyle \beta ={\frac {x_{0}\omega _{0}^{2}}{g}}}$

il coefficiente che determina il grado d'accoppiamento tra i pendoli

${\displaystyle x_{0}={\frac {mL_{cm}}{2m+M}}}$

lo spostamento della base in seguito al moto dei pendoli.

• Si osservi ora che, oltre alle non-linearità proprie di ciascun oscillatore, ora anche il termine di accoppiamento tra i metronomi è non lineare. I due termini sono governati dalle costanti ${\displaystyle \mu }$ e ${\displaystyle \beta }$.

---

---