Description

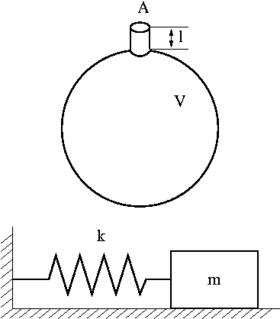
Helmholtz resonators are special resonating acoustic cavities created by Hermann von Helmholtz in 1860 to study sound and its perception. They are easily-built, metal containers (usually spherical or cylindrical) of various sizes with a short, narrow neck and narrow opening.

How it works and applications

Setting the air in a resonator into oscillation (e.g. by blowing into the mouth or by exposing the resonator to a source of sound waves) will generate stationary waves in resonance inside it with the eigenfrequency of the cavity, which then behaves like a selective sound amplifier in a narrow interval of frequencies.

1. Therefore, a resonator-bank of various sizes can be used as an analogical instrument of sound analysis. When a complex sound is present, the resonator-bank splits it into its pure components. The response of each resonator will be proportional to the intensity with which the corresponding frequency contributes to forming the sound to be analysed. It is a rudimentary mechanical system that can carry out a Fourier analysis in real time. Thanks to electronics, these operations are executed by a bank of filters that operate on an electric signal obtained from the original sound through a microphone.
2. Helmholtz was the first to use resonators in the study of the sensation of tone. He quickly discovered that a resonator-bank was a fairly accurate model of the human ear. In fact, the human ear executes a Fourier analysis of sound it receives in real time transforming the information contained in the individual harmonic components into a spatial code: harmonics of different frequencies correspond to excitation in different positions inside the cochlea. For more details, see the pages on Anatomy of the auditory system and Physiology of the auditory system.
3. The principle of the resonator can be applied to string instruments, of which it is always the hollow body (see the pages on Questions and answers about musical instruments, the violin and guitar). Helmholtz's resonance principle contributes, sometimes in a decisive way, to the acoustic quality and response of these instruments.
4. Another application is in subwoofers present in modern Hi-Fi systems. The Helmholtz resonance of an appropriately sized wood box can facilitate the transmission of a low-frequency speaker. Below 80 Hz, the transmission efficiency of classic speakers decreases drastically, and, without the help of resonance, it would be impossible to emit sound waves with high levels of intensity. There are also "tricks" based on the acoustic illusion of missing fundamental to increase the apparent efficiency of a low-frequency speaker. See the related page for an explanation.

Frequency of an ideal resonator

Just two parameters are sufficient to completely describe a resonator: its resonance frequency and the efficiency with which it resonates (i.e. the interval of frequencies at which a response is obtained). We will look at only the first because the second depends on the instrument's internal friction.

In an ideal resonator, we can suppose that, during the oscillation of the air mass, the air itself moves without friction and does not leave the container. In these hypotheses, the air in the container behaves like an ideal spring and the air in the "neck" behaves like an ideal mass. Therefore it is easy to figure out a mechanical model with "lumped elements", i.e. considering the air in the cavity body as an entity without inertia but with elasticity, while the air in the neck as an entity with inertia but with negligible elasticity.

These approximations are justified by the fact that, in the closed, rigid body of the container, air is immobile and maintains its elastic compressibility, while in the open neck air is free to move with a finite speed like a single block without modifying its volume.

Thanks to this mechanical model, we can neglect the details of the fluid dynamics and consider the oscillation like that of a system with a single degree of freedom.

Mechanical equivalent of the ideal resonator

The parameters that describe the ideal resonator are summarised in the following table.

symbol	stands for	unit of measurement in the SI system
l	neck length	m
A	neck section	m2
V	volume of bottle body	m3
ρ0	density of air at rest	kg/m2
v	speed of sound in air	m/s

The Helmholtz resonator is a bottle with a neck that is very small in relation to its body, i.e. it must be

${\displaystyle V\gg Al}$.

• The system is entirely equivalent to the mechanical mass-spring system (see the page on Analogies in physics).
• The air inside the hollow body behaves like a spring because it is compressible. The greater the volume V of the container, the less is its equivalent elastic constant (i.e. the less rigid is the system). The equivalent elastic constant (see the page on Acoustic compliance) is

${\displaystyle k={\frac {\rho _{0}c^{2}A^{2}}{V}}}$,

where c is the speed of sound in air and ρ₀ is air density.

• The air in the "neck" behaves like an oscillating mass. Its main characteristic is the inertia that it possesses once set in oscillation. Being of a small quantity, its compressibility is negligible. A narrow mouth tends to immobilise air (large inertia), while a wide mouth makes it very easy for air to move in and out of the bottle. The air mass in the resonator's neck is

${\displaystyle m=\rho _{0}lA\;}$.

The resonance frequency of the system can be deduced by means of analogy with the frequency of oscillation of a mass-spring system

${\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$.

Substituting the values calculated above, we find

${\displaystyle f={\frac {v}{2\pi }}{\sqrt {\frac {A}{Vl}}}}$

Corrections for the real resonator

• The fact that a bit of air can exit from the container during each oscillation, increases the effective inertial component and, therefore, gives rise to a non-negligible correction to the frequency. Since the net effect of the exiting of air is equivalent to having a slightly longer neck, the correction amounts to an "effective length" to be used in the frequency formula in place of the "real length" of the neck. The effective length is given by the following empirical formula:

${\displaystyle l'=l+{\frac {4}{5}}{\sqrt {A}}}$

A quantitatively different, but conceptually identical, length correction must also be applied to real wind instruments.

• The presence of viscous friction has a rather small effect on resonance frequency, which as in all oscillating systems, only depends on the balance between the system's inertial and elastic components. Friction only has effect on the quality factor of the system, i.e. on the resonance width (see the discussion on the page about resonance in general). The presence of friction along with the small exchange of internal and external air, justifies the fact that, once excited, the vibration decays after a certain time, unless more energy is continually supplied from the outside. Furthermore, the greater the friction, the greater will be the interval of frequencies in which the resonator responds. When friction forces are large, the resonator is less selective in frequency.
• The role of friction and turbulent motion are quite different regarding the "setting in vibration" of the resonator. In fact, rather than "responding" to an external sound source by resonance, the Helmholtz resonator can be excited by blowing on the edge of its mouth. For more details on how continuous air flow can transform into an oscillating pressure wave, see the pages on the flute, whistle and ocarina.

Simulation of the response

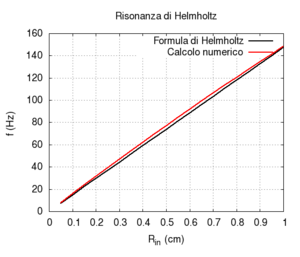
We carried out a simulation of the response of a cylindrical Helmholtz resonator and compared the numerical results with the Helmholtz formula discussed in the preceding paragraph. We observed only small deviations from the values predicted by Helmholtz, once the mouth length was corrected to account for the exiting of air. Let us recall that the formula is valid only when the cavity volume is much greater than the mouth volume, while the correction of effective length is just an elementary approximation. Of course, when the mouth is much larger, the radiation effect becomes more important, while, for small sections, we need to account for the effects of viscous friction in the simulation of a real resonator. We have not accounted for these effects here.

We first studied the dependence of resonance frequency on the mouth section. Contrarily to what we might expect but in agreement with Helmholtz predictions, frequency increased as the mouth section widened.

Geometry	Acoustic response	Resonance

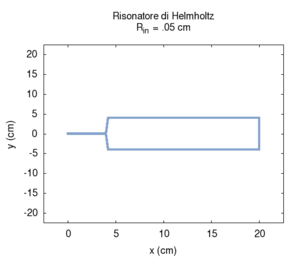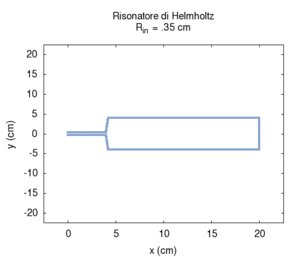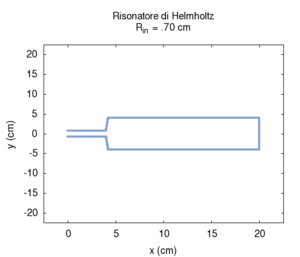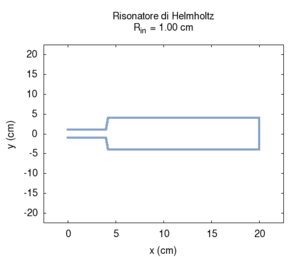
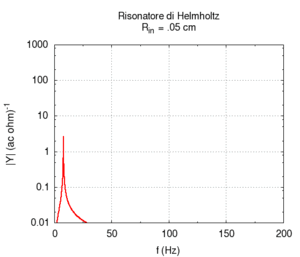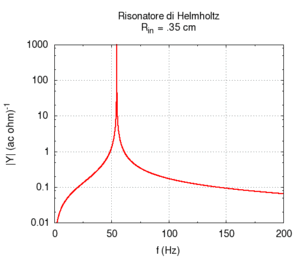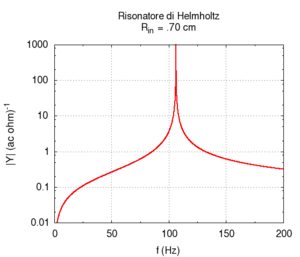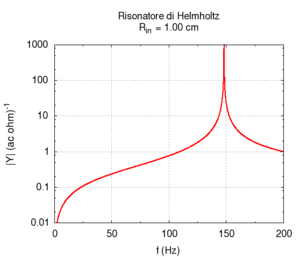
The second effect is more known: increasing the volume of the resonator causes its resonance frequency to become lower. This determines the typical structure of resonator-banks, which were once used as filters, in long lines of progressively increasing size. This structure is actually characteristic of all musical instruments that produce sound based on resonator-banks, such as the piano, organ or (even if in a more approximate meaning) the entire orchestra. Note that in the calculation, the greatest error in numerical calculation is in the large transversal size of the cavity. This error can be mainly attributed to the simplifying assumption that stationary waves in the cavity can only be created along the cylinder's axis.

Geometry	Acoustic response	Resonance

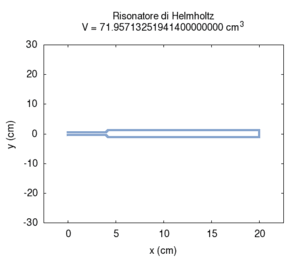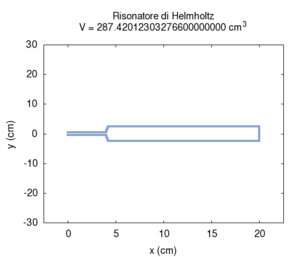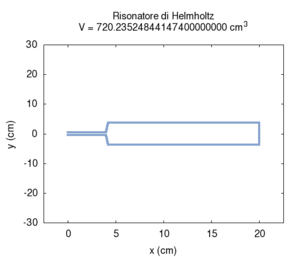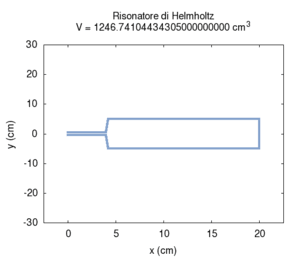
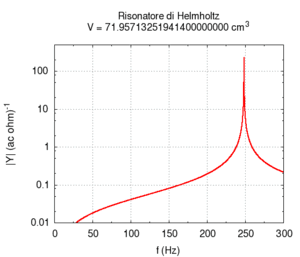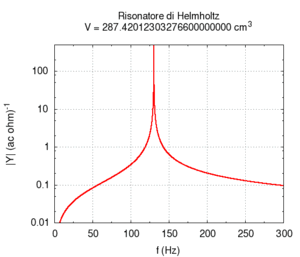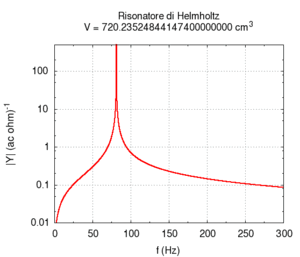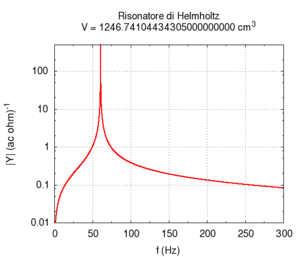
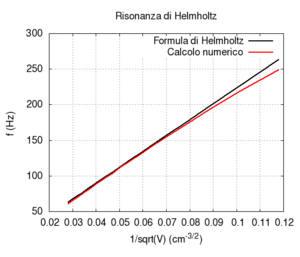
In-depth study and links

• Other pages offer more information on resonating cavities and the role of resonance in musical instruments.
• See the page on the whistle and ocarina, which are the only instruments in which sound is entirely determined by Helmholtz resonance.
• Fourier's Theorem provides the rigorous mathematical basis for the decomposition of a sound into pure sounds.
• Use our virtual laboratory applet to design your own sound wave, analyse its component frequencies, listen to the corresponding sound and change it as you like.

---