The sound source of chordophones is a group of strings (which were once made of catgut and are now steel, nylon or other materials) held taut between two fixed points. String instruments are distinguished by classes depending on how the strings are excited to produce sound. There are plucked, bowed and struck string instruments.

String instruments (chordophones)
With plucked strings	With struck strings	With bowed strings
Harp Harpsichord Lute Guitar Mandolin Banjo	Piano Spinet	Violin Viola Cello Contrabass

"Notes" on Physics

Elastic strings have the property of oscillating freely at a well-defined frequency that is determined by their tension and density. However, there is a clear difference in the sound quality between such string instruments as the guitar, violin and piano. The factors that contribute to this difference are many and complex. Here, we will briefly examine the characteristic of the vibration of strings when they are excited in three different ways. To read a more detailed discussion of individual instruments, visit their dedicated pages.

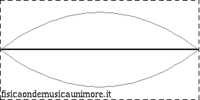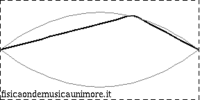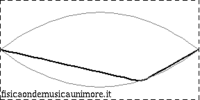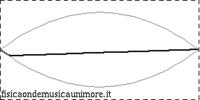
Plucked strings	Struck strings	Bowed strings
The string is initially forced to assume a shape that is basically triangular and is then left free to oscillate.	The string is initially forced to assume a shape that depends on time, impact force and impact position and is then left free to oscillate.	The string is maintained in oscillation by the action of the bow.
The intensity of the oscillations decays exponentially over time.		The intensity of the oscillations over time depends on the action of the bow.
The fundamental frequency is equal to the frequency of the free oscillation (see Eigenfrequencies of strings)		Even if the oscillation is not free but forced, the fundamental frequency is equal to the frequency of the free oscillation.
The spectrum contains all the harmonics: in none of the three cases is the oscillation simple nor does the string oscillate according to a particular normal mode; rather it oscillates in a superposition of (infinite) modes
The 'nth harmonic has an amplitude proportional to ${\displaystyle {\frac {1}{n^{2}}}}$.	The 'nth harmonic has an amplitude proportional to ${\displaystyle {\frac {1}{n}}}$.	The 'nth harmonic has an amplitude proportional to ${\displaystyle {\frac {1}{n^{2}}}}$.
All normal modes that would have a node at the plucking/impact/friction point are suppressed.

Musical "notes"

With plucked strings

The strings of these instruments are generally placed on a resonating cavity and are plucked by fingers only. The harp is perhaps the most iconic member of this family and, since the 19th-century, has become an indispensable element of orchestration because it can add a variety of effects including highlighting accents and adding depth of timbre. It is also famous for the glissando, its most typical articulation, which is a characteristic and evocative brush of colour that we can hear in the famous Waltz of the Flowers from the Nutcracker by P. I. Tchaikovsky. Thanks to the advent of electronics, the guitar is the instrument that has perhaps most benefited from technological-acoustic evolution. In fact, both amplification and the addition of effects of all types have radically changed its sound and given rise to a wide variety of timbres that range from the sweet and soft traditional colour heard in Study no. 1 by H. Villa Lobos to the hardness and harshness of avant-garde rock heard in Money for Nothing by the Dire Straits.

Ciaikovskij_valzer_dei_fiori.mp3 Čaikovskij, from Schiaccianoci

Villa_Lobos_studio_1.mp3 Villa Lobos, from studio n. 1

Dire_Straits_Money_for_nothing.mp3 Dire Straits, from Money for nothing

With struck strings

As their name itself says, these instruments are based on the mechanics of strings, which are usually located within a resonant body and are made to vibrate by various types of sticks or hammers. The piano is obviously the most representative example of this group and, thanks to its slow but constant technical evolution over more than a century, allows for a multiplicity of timbre tones that can make it a valid substitute for the orchestra. In the 18th century, the piano had a clear and crystalline sound such as the one in this Three Voice Invention no. 8 by J. S. Bach (similar to the harpsichord). With the addition of the resonance pedal, the edges of its sound became less defined and even reached, in the so-called “impressionist” period, a colour that was so sfumato as to almost be “turbid” as in Mirrors by M. Ravel. During the 20th century, as a reaction to this aesthetic tendency, which was considered by some to be “degenerate”, the piano re-acquired the percussive sharpness of its original timbre (for an example, listen to Out of Doors by B. Bartók). Of particular interest amongst instruments of popular origin (which are also becoming more common in cultured circles) is the spinet; that strange, trapezoidal-shaped box that we sometimes see being played in the underground and that we can hear in this sample of Un Brin de Bruyère by G. Kurtág.

Ciaikovskij_valzer_dei_fiori.mp3 Čaikovskij, from Schiaccianoci

Villa_Lobos_studio_1.mp3 Villa Lobos, from studio n. 1

Dire_Straits_Money_for_nothing.mp3 Dire Straits, from Money for nothing

With bowed strings

The members of the bowed string family include the violin, viola, cello, contrabass and all instruments of popular origin or those belonging to other eras and civilizations that are based on the principle of rubbing (usually with a bow) and making taut strings mounted on a resonating cavity vibrate to generate sound waves. The usual use of these instruments is for a lyrical effect (as in the heart-wrenching beginning of the Fourth movement of the Pathetique symphony by P. I. Tchaikovsky), thanks to the expressivity created by the pressure of the bow (which varies the sound volume) and vibrato (which adds warmth and “life” to its sound). These instruments offer many types of sound emissions with varying and surprising results. One of the most outstanding of these is the pizzicato; a technique used primarily in a cultured repertory, however, now also increasingly in a popular repertory (such as in the famous Fourth movment of Peer Gynt Suite no. 1 by Grieg, which also became the theme song of a famous television cartoon).

Ciaikovskij_sinfonia_6_IV.mp3 Čaikovskij, from Synphony n. 6 Patetica

Grieg_peer_gynt.mp3 Grieg, from Peer Gynt

---