La dispersione è il fenomeno per cui, in un dato mezzo, la velocità di propagazione di un'onda dipende dalla sua lunghezza d'onda. La particolare legge che, di caso in caso, descrive la dipendenza della velocità dalla lunghezza d'onda si chiama legge di dispersione.

La legge di dispersione si può rappresentare in molti modi, perché le onde sono descritte da molte grandezze diverse non tutte indipendenti tra loro (vedi grandezze fondamentali delle onde). Tipicamente nelle applicazioni si usa indicare la dipendenza della frequenza dalla lunghezza d'onda.

Come si manifesta la dispersione

Per capire l'essenza di questa proprietà del mezzo osserviamo le animazioni qui sotto:

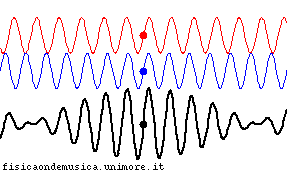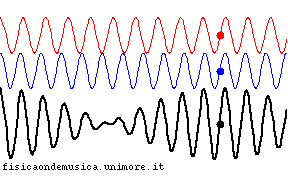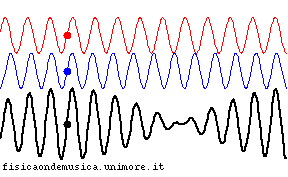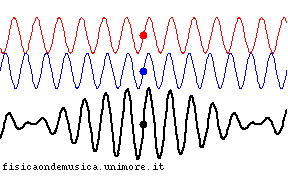
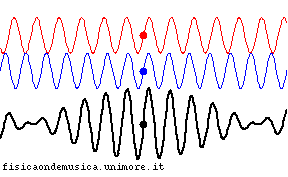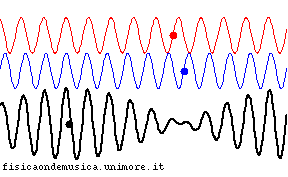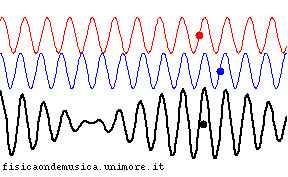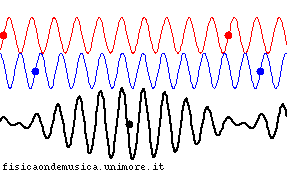
• in entrambe le animazioni la linea nera è la somma delle due linee colorate. Ciascuna linea colorata è una semplice sinusoide, ma le due hanno lunghezze d'onda leggermente differenti (in rapporto di 11:10).
• Entrambe le animazioni partono nello stesso stato iniziale, cioè le onde colorate sono sovrapposte in modo da formare la stessa identica figura all'istante iniziale.

Si osserva che:

1. nel mezzo non dispersivo le due componenti colorate avanzano con la stessa velocità. Di conseguenza la loro fase relativa rimane invariata, e, di conseguenza, anche la linea nera (la somma delle componenti) avanza con la stessa velocità senza cambiare forma durante la propagazione;
2. nel mezzo dispersivo, al contrario, la sinusoide blu avanza più velocemente di quella rossa, e perciò la loro fase relativa cambia nel tempo. Ciò si traduce nel fatto che, col passare del tempo, il segnale somma (linea nera) non compie una semplice traslazione nello spazio, ma cambia completamente forma.

Per evidenziare la velocità della propagazione del segnale in entrambe le animazioni si è segnalato con un punto nero il massimo dell'onda risultante (se si trattasse di un esempio acustico esso coinciderebbe con il punto in cui il battimento tra le due componenti ha la massima intensità).

sovrapposizione di due onde armoniche di diversa frequenza
mezzo non dispersivo	mezzo dispersivo

Conseguenze e applicazioni

Finora l'unica conseguenza apparente del fenomeno della dispersione sembra essere il fatto che il segnale risultante si propaga nei due casi con due velocità diverse. Di fatto le due velocità sono indicate in fisica con nomi diversi:

• la velocità con cui si propaga ciascuna componente armonica è detta velocità di fase, mentre
• la velocità con cui si propaga il battimento tra le due (o, più in generale, l'inviluppo dell'onda risultante) è detta velocità di gruppo.

Si osservi, nel caso precedente, che la velocità di gruppo è maggiore di entrambi le velocità di fase, ma, utilizzando una differente dispersione (cioè modificando la dipendenza della velocità di fase dalla lunghezza d'onda), è possibile produrre sovrapposizioni in cui la velocità di gruppo è minore o uguale a quella di fase, o anche un battimento stazionario con velocità di gruppo nulla. Nel mezzo non dispersivo, invece, velocità di fase e di gruppo sono sempre uguali.

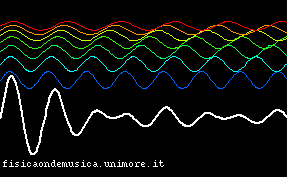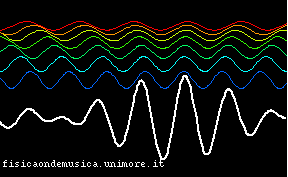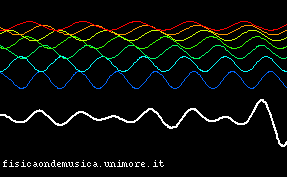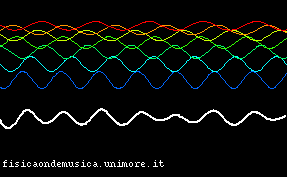
Questo fenomeno, lungi dall'essere una mera curiosità, diviene importantissimo nel caso delle telecomunicazioni (sia quelle basate sulle onde elettromagnetiche, sia quelle acustiche, come quelle verbali o musicali). Questo diviene meglio evidente quando si sovrappongono più di due frequenze. Nell'esempio che segue si schematizza la propagazione della luce bianca in un mezzo dispersivo. I colori delle componenti corrispondono alle lunghezze d'onda. Come per la vera luce visibile al rosso corrisponde la massima lunghezza d'onda, al violetto la minima.

Mezzo non dispersivo	Mezzo dispersivo
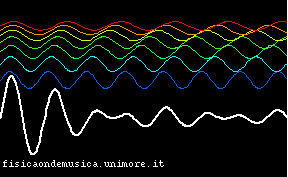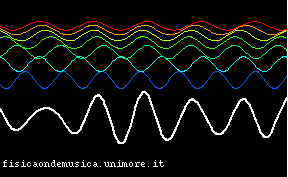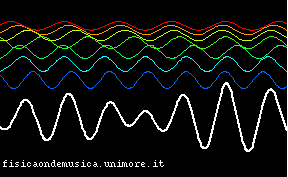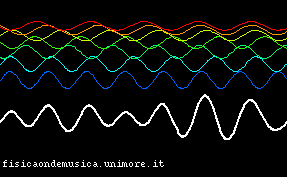
Le onde di tutti i colori si propagano con la stessa velocità	Le onde di colori diversi si propagano con velocità diverse

È facile ora vedere l'importanza di questo fenomeno nelle applicazioni: supponiamo che la curva in bianco sia un segnale che vogliamo trasmettere da un posto ad un altro (per esempio una trasmissione radio, o una parola, se ci riferiamo alle onde acustiche). È evidente che, se la linea di trasmissione è non dispersiva, il segnale si propaga senza cambiare forma, ed è quindi possibile trasmetterlo a distanza in modo fedele all'originale, e non distorto. Infatti, si vede che l'inviluppo della curva bianca trasla verso destra nell'animazione. Invece, quando il mezzo è dispersivo il segnale originale non può essere ricevuto, perché, durante il tragitto, esso ha cambiato forma.

Entrambi le animazioni partono dallo stesso stato iniziale, in cui la sovrapposizione delle onde monocromatiche produce un segnale con un inviluppo ben definito (simile a quello delle prime animazioni della pagina), ma si vede che, mentre nel mezzo non dispersivo il massimo si conserva, spostandosi in blocco verso destra, nella seconda animazione si nota che il segnale si sparpaglia ben presto, perdendo la sua caratteristica iniziale.

Approfondimenti e collegamenti

In una notissima esperienza Newton dimostrò che la luce solare è in realtà una mescolanza di luce di vari colori. Egli, tramite un prisma, sfruttando il fenomeno della rifrazione riuscì a scomporre un fascio di luce solare nei suoi colori componenti.

Il fenomeno si può interpretare semplicemente ammettendo una dipendenza dell'indice di rifrazione dal "colore della luce" che investe la superficie di separazione tra i due mezzi. Secondo la teoria ondulatoria, che associa ad ogni "colore" una ben determinata lunghezza d'onda all'interno dello spettro elettromagnetico, tale dipendenza sarà da imputarsi ad una dipendenza della velocità di propagazione nel mezzo denso dalla lunghezza d'onda dell'onda stessa.

• Un fenomeno naturale in cui la dispersione produce un effetto spettacolare è l'arcobaleno, cui è dedicata una pagina a parte che ne illustra alcuni dettagli.
• Anche le onde che si propagano alla superficie di separazione tra due mezzi sono in genere dispersive anche se i due mezzi presi separatamente non lo sono. L'esempio più noto è costituito dalle onde sulla superficie dell'acqua. È noto infatti che le onde più lunghe si propagano più rapidamente di quelle più corte. Per scoprire la particolare relazione di dispersione in questo caso si veda la pagina equazione delle onde nell'acqua.
• Un altro tipo di onde di superficie (che si propagano quindi con dispersione) è costituito dalle cosiddette Onde di Rayleigh, che si osservano alla superficie della crosta terrestre durante i terremoti. Si veda in proposito velocità delle onde meccaniche, ed onde trasversali e longitudinali.
  
  
• La dispersione nel vetro e nei materiali trasparenti ha particolare rilevanza per tutti gli apparecchi ottici (obiettivi di macchine fotografiche, o di binocoli e telescopi). Infatti, se la dispersione non è adeguatamente compensata, in questi strumenti si possono verificare artefatti e distorsioni dell'immagine note come "aberrazione cromatica". Nelle fotografie scattate con macchine economiche essa è evidente alla separazione tra un oggetto scuro e uno chiaro (tipicamente il cielo), lungo il quale si vedono piccole righe colorate.
• Anche quando un mezzo infinito è privo di dispersione, è possibile costruire configurazioni confinate che manifestano dispersione. È il caso delle guide d'onda. Esse sono delle "piste" in grado di propagare un certo tipo di onde lungo un percorso prefissato. Per le onde elettromagnetiche sono guide d'onda le fibre ottiche, e certi tipi di antenna; per le onde acustiche sono guide d'onda le canne degli strumenti a fiato. Come è illustrato in dettaglio nella pagina guide d'onda, caratteristiche comune di tutti questi dispositivi è l'esistenza di una frequenza limite sotto la quale le onde non possono propagarsi. Con il linguaggio della dispersione possiamo dire che ciò avviene perché esiste una frequenza limite al di sotto della quale la velocità di propagazione diviene pari a zero. Notiamo che, in questi casi, la dispersione non dipende solo dalle proprietà fisiche del mezzo che trasporta l'onda, ma anche dalla particolare configurazione geometrica delle pareti che lo limitano (in particolare dalla loro forma e dimensioni).
• Similmente a quanto accade per le guide d'onda, osserviamo il fenomeno della dispersione anche quando un'onda si propaga in un mezzo discreto anziché in uno continuo. Più precisamente, il fenomeno diventa rilevante per le onde la cui lunghezza è paragonabile alla distanza tra due successivi elementi discreti del mezzo. In caso contrario il mezzo può essere trattato come un continuo. Si pensi ad un solido come ad un reticolo atomico, o anche, più semplicemente, ad una catena di oscillatori armonici. Come è descritto in maggior dettaglio alla pagina equazione delle onde nella catena di oscillatori, anche in questo caso si osserva che onde di diversa lunghezza si propagano con diverse velocità, e che esistono "bande proibite", corrispondenti ad intervalli di frequenza per cui le onde non possono propagarsi del tutto nel mezzo.

---