"Vedere" e "osservare" un arcobaleno

Avete sicuramente visto più volte un arcobaleno. Siete sicuramente rimasti affascinati dallo spettacolo, ma pensate di averlo guardato bene? Per esempio a quante delle seguenti domande sapreste rispondere?

1. Quanto è grande un arcobaleno? Cioè quanto è alto sull'orizzonte?
2. Qual è il raggio dell'arco descritto dall'arcobaleno?
3. Qual è la sequenza dei colori? Il rosso sta all'interno o all'esterno?
4. A volte si vede un secondo arco. Le precedenti domande valgono anche per questo.
5. C'è anche un terzo arco e un quarto, ecc...?
6. Il sole sta alle nostre spalle o davanti a noi?
7. Si vede qualcosa sotto l'arco principale?

Fin dal XIII secolo era noto che l'arcobaleno fosse prodotto dalle gocce d'acqua in sospensione nell'aria, per esempio dopo i temporali. Isaac Newton, nel suo trattato di ottica, dimostrò che la luce bianca può essere scomposta da un prisma in componenti monocromatiche, e diede così una spiegazione del fenomeno. La sua teoria, però si basava sull'idea che la luce avesse una natura corpuscolare, e, come vedremo in seguito, questo impedisce di descrivere alcune caratteristiche speciali del fenomeno.

Dapprima mostreremo il ragionamento di Newton, e poi cercheremo di scoprire cosa tutto questo ha a che fare con le onde.

Risposte dall'ottica geometrica

Se le gocce d'acqua hanno diametro di qualche millimetro, la spiegazione della formazione e delle caratteristiche dell'arcobaleno può essere svolta interamente applicando l'ottica geometrica.

Rifrazione da una goccia

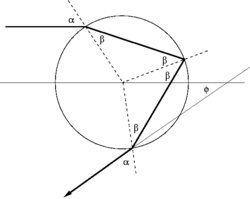
Consideriamo dapprima la rifrazione della luce bianca da parte di una goccia. Scegliamo l'asse x lungo la direzione da cui proviene la luce.

Riferendosi al disegno, per cui il raggio luminoso indica il cammino di un fronte d'onda nella goccia, vale la legge della rifrazione (o di Snell)

${\displaystyle \sin \alpha =n\sin \beta \!}$,

dove

${\displaystyle n={\frac {n_{\rm {acqua}}}{n_{\rm {aria}}}}}$,

e l'indice di rifrazione dell'aria vale circa 1, mentre quello dell'acqua varia a seconda del colore. In media vale 1.336, variando da 1.331 per il rosso a 1.343 per il violetto.

L'angolo φ di uscita dalla goccia rispetto alla direzione di ingresso si può esprimere in termini degli angoli di incidenza α e di rifrazione β come

${\displaystyle \phi =4\beta -2\alpha \!}$

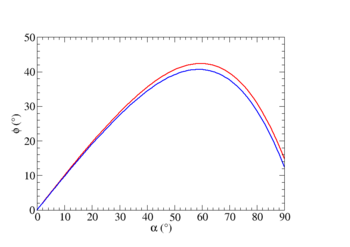
Sostituendo la legge di Snell nella precedente, e tracciando il grafico di φ in termini dell'angolo di incidenza α (vedi figura) osserviamo che :

• per α=0 la luce viene riflessa all'indietro.
• all'aumentare di α φ inizialmente cresce. Ma per α≈60° φ raggiunge un valore massimo che dipende dal colore.
• Per valori di α superiori l'angolo φ torna a diminuire.

Il valore di α per cui φ è massimo si trova risolvendo

${\displaystyle {\frac {d\phi }{d\alpha }}=0}$,

che dà

${\displaystyle \cos ^{2}\alpha ={\frac {n^{2}-1}{3}}}$,

Ora, per ogni colore siamo in grado di calcolare l'angolo di incidenza per cui l'angolo di uscita dalla goccia d'acqua è massimo (vedi tabella)

colore	n	${\displaystyle \alpha }$	${\displaystyle \beta }$	${\displaystyle \phi _{\rm {max}}}$
rosso	1.331	59°53'	40°36'	42°37'
...	...	...	...	...
violetto	1.343	58°83'	39°58'	40°65'

Ciò significa che l'angolo maggiore si ha per il rosso, e il minore per il violetto.

La goccia ha simmetria sferica, quindi questi angoli definiscono dei coni, che delimitano la regione entro cui ogni colore può essere rifratto.

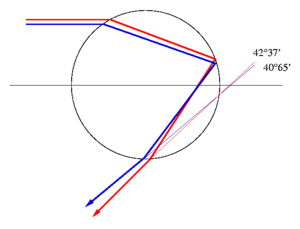
Per angoli minori di 40°65' tutti i colori vengono rifratti, e quindi la luce originale bianca resta bianca. La luce, invece, non può uscire dalla goccia per angoli maggiori di 42°37'.

Quindi:

• l'ampiezza massima dell'arco è di circa 42°37'. Questo angolo si calcola rispetto all'elevazione del sole. Perciò all'alba o al tramonto l'arcobaleno è più grande, mentre è praticamente invisibile a mezzogiorno.
• il rosso occupa l'arco più esterno, mentre il violetto sta all'interno ad un angolo di 40°65'.

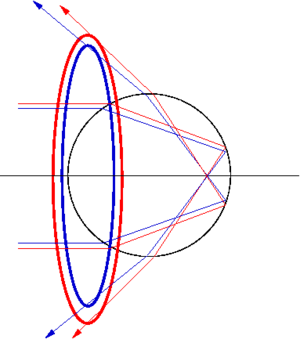
Ad angoli superiori il raggio luminoso della figura può compiere il percorso inverso. Questo produce il secondo arcobaleno. Questa volta il ragionamento è invertito, e perciò esiste un angolo φ minimo, anziché uno massimo.

• Il secondo arcobaleno sta all'esterno del primo. Il rosso sta all'interno con un angolo di 50°37', mentre il violetto all'esterno con un angolo 53°47'.

Oltre l'arcobaleno: risposte dall'ottica ondulatoria

Se il diametro delle gocce è più piccolo (circa 1 mm), l'interferenza delle onde luminose all'interno delle gocce diventa importante, e bande oscure possono apparire all'interno dell'arcobaleno, a causa delle zone in cui l'interferenza distruttiva.

Per gocce di diametro compreso tra 0.1 mm e 50 μm gli effetti della diffrazione diventano rilevanti.

Per gocce di diametro inferiore a 50 μm la diffrazione impedisce la separazione dei colori, ma non la riflessione della luce, e si ha il cosiddetto "arcobaleno bianco".

---