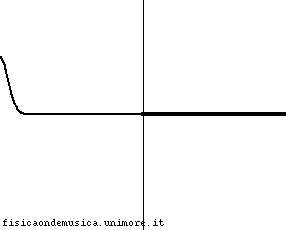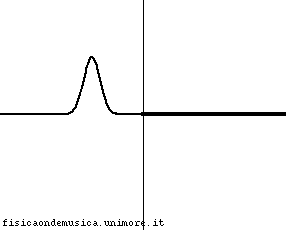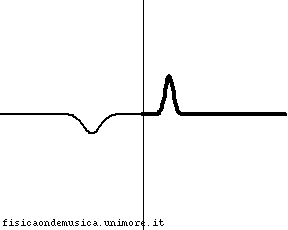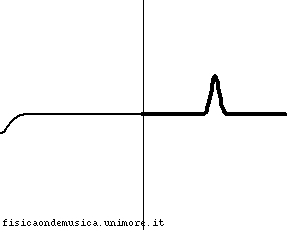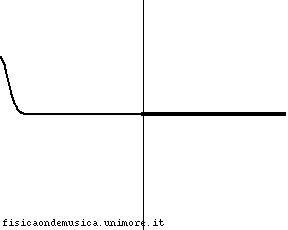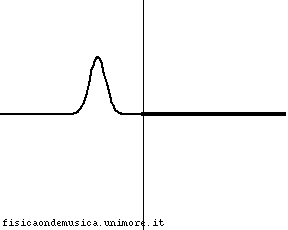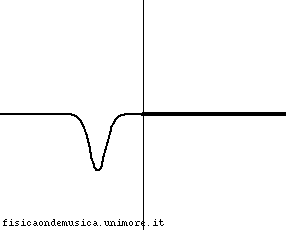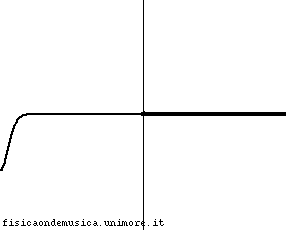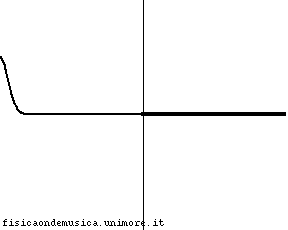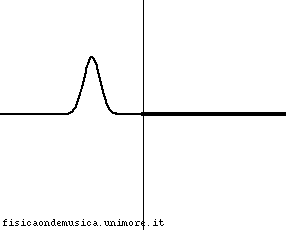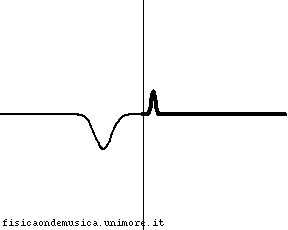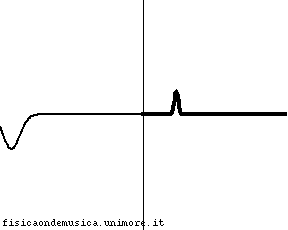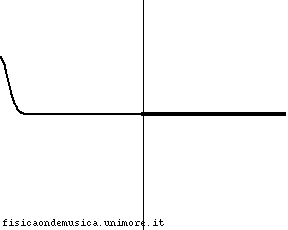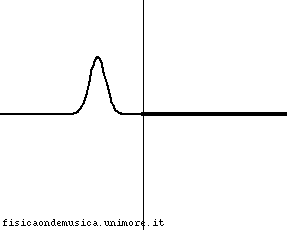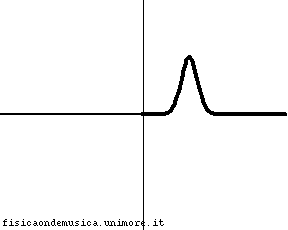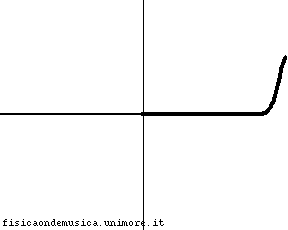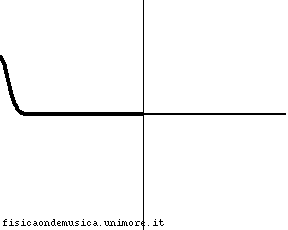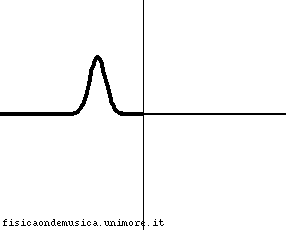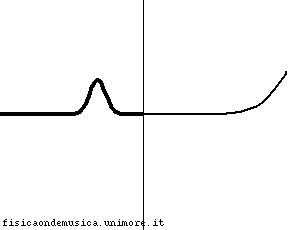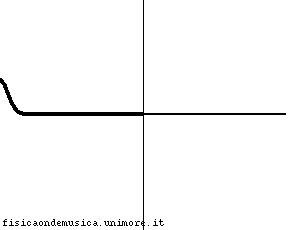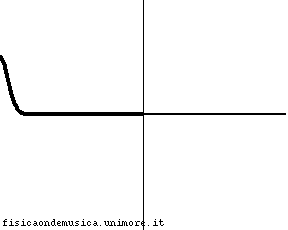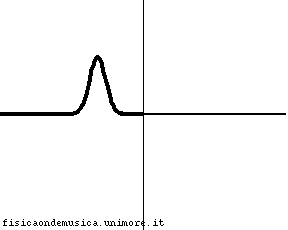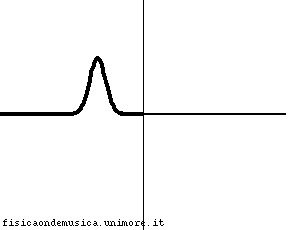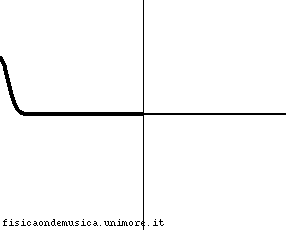• Quando un'onda passa da un mezzo ad un altro in cui la sua velocità di propagazione cambia, alla superficie di separazione dei due mezzi accadono fenomeni interessanti: l'onda sembra "sdoppiarsi". Una parte viene riflessa indietro nel primo mezzo, mentre un'altra può penetrare nel mezzo, ma le sue caratteristiche (ampiezza, velocità, direzione di propagazione, lunghezza d'onda) sono diverse da quelle dell'onda incidente.
• Vogliamo qui indagare che relazioni esistono tra l'onda incidente e le due onde prodotte, che chiameremo riflessa (quella che torna indietro nel primo mezzo), e rifratta quella che penetra nel secondo mezzo. Per esaminare il caso più semplice possibile studiamo il fenomeno in una sola dimensione.

Rifrazione delle onde in una corda

• Consideriamo due tratti di corde di diversa densità saldate l'una di seguito all'altra. Facciamo un piccolo sforzo di astrazione immaginando che entrambi le corde siano ideali, e che la giunzione sia una saldatura anch'essa ideale. Questo sforzo è ricompensato dal fatto che tutti i calcoli sono più semplici in queste ipotesi. Per esempio, possiamo dire che la tensione T è la stessa lungo tutta la corda composta risultante.
• Le onde si muovono con velocità diverse nelle due corde prese separatamente, infatti (vedi equazione delle onde nella corda, frequenze proprie della corda e velocità delle onde meccaniche), dette ρ₁ e ρ₂ le rispettive densità, abbiamo

;

Ora consideriamo un'onda che percorra la corda composta dal tratto di tipo 1 verso il tratto di tipo 2. Essa attraverserà il primo tratto con velocità v₁, ma, giunta al punto di discontinuità la (la saldatura tra le due corde), l'onda è in parte riflessa e in parte trasmessa. Quale frazione dell'onda incidente è riflessa e quale frazione è trasmessa è indicato da due coefficienti numerici detti coefficiente di trasmissione e coefficiente di riflessione, al cui calcolo è dedicata una sezione a parte (trasmissione e riflessione). Essi sono

,

(5)

.

(6)

Ora, per cogliere il significato dei coefficienti visualizziamo vari casi:

			propagazione	commento
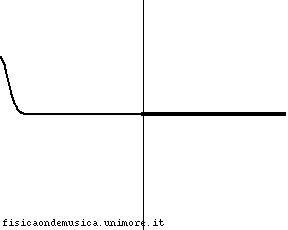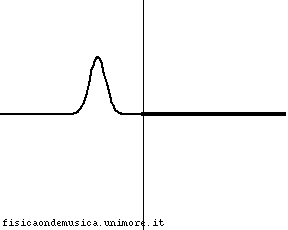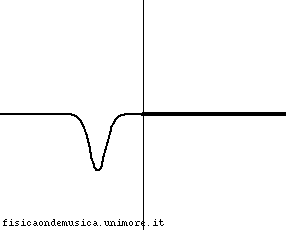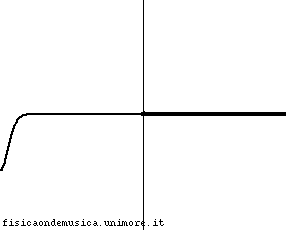
				L'impulso viaggia con velocità molto minore nella corda 2 rispetto alla corda 1. Possiamo dire, compiendo un errore trascurabile, che esso non si propaga affatto nella seconda corda, o, equivalentemente, che la corda 2 ha impedenza infinita. L'onda incidente viene quasi completamente riflessa con inversione di fase, e l'onda trasmessa è praticamente nulla. Il coefficiente di trasmissione è molto vicino a 0, mentre il segno - del coefficiente riflessione indica che c'è inversione di fase.
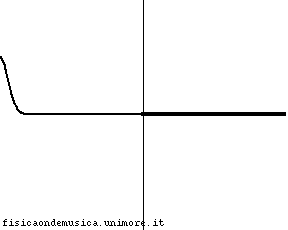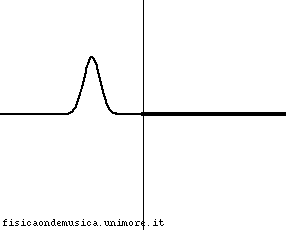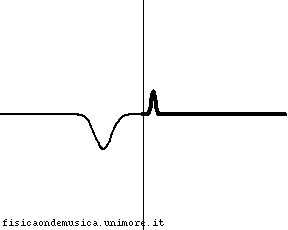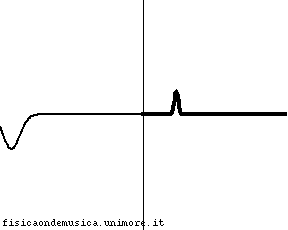
				Sia l'onda riflessa sia l'onda trasmessa non sono nulle. L'onda riflessa ha fase opposta rispetto all'onda incidente ed ampiezza minore. L'energia dell'onda incidente è ripartita tra l'onda riflessa e quella trasmessa.
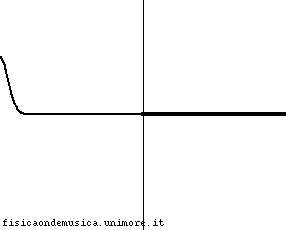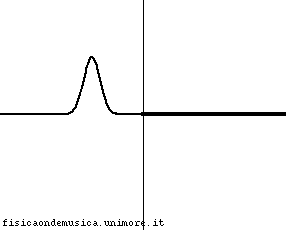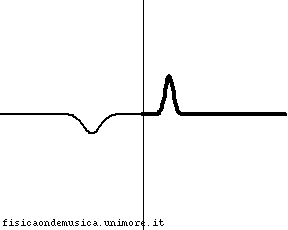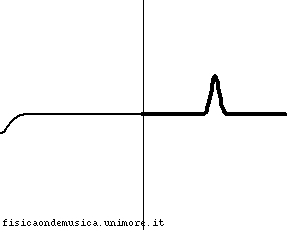
				Come il caso precedente, ma l'onda trasmessa è maggiore. Una parte maggiore dell'energia si trasferisce dalla corda 1 alla corda 2.
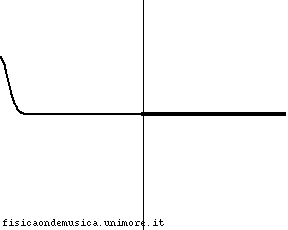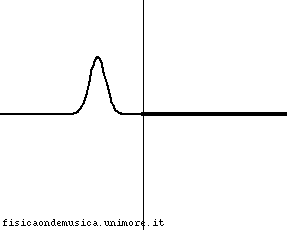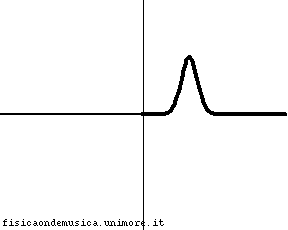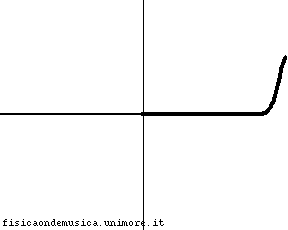
				Le due corde hanno la stessa densità, quindi, in realtà, si tratta della stessa corda. Non essendo presente la discontinuità l'impulso viaggia indisturbato. L'onda riflessa si annulla, e l'energia fluisce liberamente da sinistra a destra. Il coefficiente di riflessione è quindi nullo, mentre quello di trasmissione uguale ad 1.
				Compare una piccola onda riflessa avente la stessa fase dell'onda incidente. L'energia dell'onda incidente è ripartita tra l'onda riflessa e quella trasmessa, ma, per la maggior parte è ancora trasmessa.
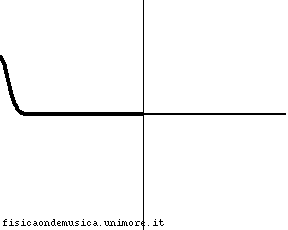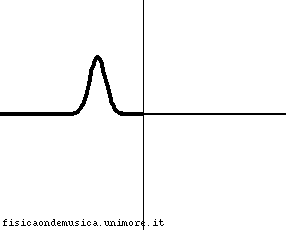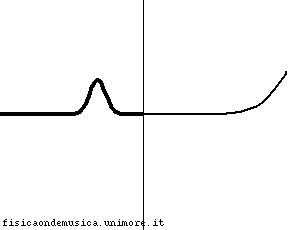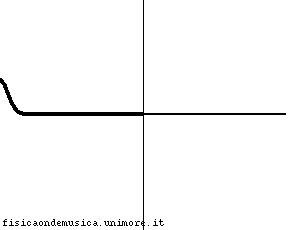
				Come il caso precedente, ma l'onda riflessa è maggiore. Una parte maggiore dell'energia rimbalza dalla discontinuità indietro verso la corda 1.
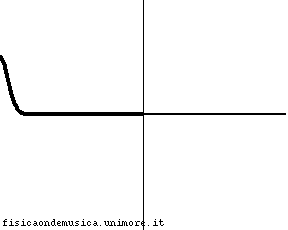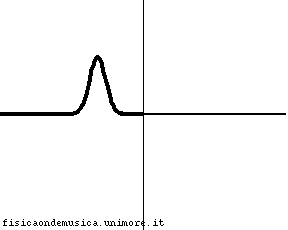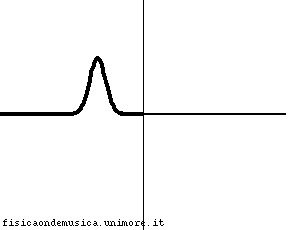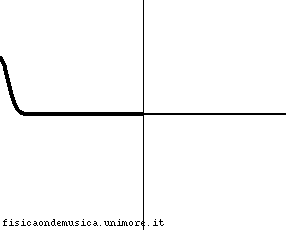
				L'impulso viaggia con velocità molto maggiore nella corda 2 rispetto alla corda 1. Possiamo dire, compiendo un errore trascurabile, che la corda 2, è infinitamente "leggera", o, equivalentemente, che ha impedenza nulla. Non avendo inerzia essa si adatta immediatamente al moto dell'estremo destro della corda 1. L'onda incidente viene quasi completamente riflessa senza inversione di fase, e l'onda trasmessa interessa quasi simultaneamente tutta la corda 2. Il coefficiente di riflessione è molto vicino ad 1.

Nelle immagini precedenti, per facilità di visualizzazione si mostra la propagazione di un singolo impulso (gaussiano). Questo caso non differisce dal caso in cui si propaghino onde armoniche, perché le onde in una corda ideale hanno tutte la stessa velocità. Diverso sarebbe il caso di una corda reale, in cui gli impulsi, a causa del fenomeno della dispersione, cambiano forma durante la propagazione in ciascun mezzo.