Perception and compression of data

Psychoacoustics is a science that deals with perceived sound rather than physical sound. Along with the interest it holds for pure research in the fields of physiology and psychology of perception, this science is particularly relevant in our era, where the reproduction, transmission and manipulation of electronic sounds permeates an ever greater part of our lives. Firstly, we must realise how extremely cumbersome sound information is. The following examples will illustrate this point:

Object	Coding	Information size
A large book with 5 million characters (about the size of the Bible)	ASCII (text-only format with 1 byte per character)	5,000,000 bytes (about 4.8 MB)
A large colour photograph at 1280x1024 pixels	Resolution with 16 million colours (i.e. 24 bits per pixel)	3,932,160 bytes (about 3.75 MB)
One minute of music	To not lose any perceptible sounds, we must sample at 44.1 kHz in stereophony with a dynamic range of at least 16 bits per sample.	10,584,000 bytes (about 10 MB)

Of course, we can compress information and lose quality, which is exactly what happens in the majority of cases. Below is a table with indicative quality parameters of several audio communication media. Notice, in particular, the case of the telephone, which has a bandwidth that is just sufficient enough to transmit voices with reasonable intelligibility but is completely inadequate for the transmission of music. Voices remain intelligible, even if they are distorted, as long as the transmission remains within the spectral region of the formants; i.e. lower than 5 kHz.

Medium	Sample frequency (kHz)	Bits per sample (bit)	Transmission velocity of information (kB/s)	Information size in one minute of music
Telephone	8	8 (mono)	8	480 kB
AM Radio	11.025	8 (mono)	11	660 kB
FM Radio	22.050	16 (stereo)	88.2	5.3 MB
CD	44.1	16 (stereo)	176	10.6 MB

We can see that it is crucial that we develop coding techniques that allow for the compression of information and the reduction of the space it occupies without losing sound quality. Compression algorithms, such as ZIP programmes, are extremely efficient in compressing text files and are algorithms without information loss; i.e. the original file can be entirely recovered by inverting the algorithm. However, zip programmes do not function well with audio files.

Psychoacoustics will now intervene.

Substantially, the idea is if we can identify the less perceptible components in un audio signal, we can simply eliminate them from the signal and thereby reduce the corresponding file size without the signal losing its apparent quality. This is how the popular MP3 format was born.

Be careful, though: you have probably noticed that the algorithm explicitly allows the compressed signal to lose information. Once the irrelevant psychoacoustic components have been determined and eliminated, they will disappear from the file and cannot be recovered. This explains why it is not advisable to apply MP3 compression twice in a row or uncompress and compress back because one level six compression is not equivalent to two level three compressions. However, audio compression formats without information loss do exist, such as FLAC, but they have lower compression indexes than MP3.

Here is an example of the same song (the Toccata from the Favola d'Orfeo by Claudio Monteverdi) compressed at increasingly higher levels. The original is 1.6 MB in CD-quality WAV format and 916 kB in FLAC format (compressed without information loss). You will notice that, below 128 kbit/s, MP3 compression becomes so hard that it degrades the sound quality of the sample.

Sample bit rate size	Audio	Sonogram (NB: the frequency scale changes)
44.1 kHz (stereo) 256 kbit/s 300 kB	orfeo-256.mp3 256 kb/s
44.1 kHz (stereo) 128 kbit/s 150 kB	orfeo-128.mp3 128 kb/s
24 kHz (stereo) 64 kbit/s 75 kB	orfeo-64.mp3 64 kb/s
16 kHz (stereo) 32 kbit/s 38 kB	orfeo-32.mp3 32 kb/s
8 kHz (stereo) 16 kbit/s 19 kB	orfeo-16.mp3 16 kb/s
8 kHz (mono) 8 kbit/s 9.3 kB	orfeo-8.mp3 8 kb/s

Psychoacoustics, through the concept of critical bands, allows us to understand and exploit the main reason why the compression efficiency of MP3 is so good; it is known as masking.

Masking

On many pages in the section on Physics of Waves, we highlighted the importance of the superposition principle and applied it to case studies. We have stressed that it is a very useful working hypothesis. This is a very important approximation both because it can be applied to many experimental situations and because its use opens the door to a vast series of mathematical results and techniques of great importance to all of physics and, in particular, to wave physics.

In the case of sounds, we can summarise the principle as follows:

in the place in space where two simultaneous sounds meet, the resulting sound is the (algebraic) sum of the two incident sounds.

The principle is very intuitive, at least for sounds that are not too intense, because we know that sound is nothing more than a small pressure variation and, therefore, it is natural that two simultaneous pressure variations in one point give a pressure variation equal to the sum of the two. The beauty of the superposition principle is that it can also be used "backwards": a given sound can be decomposed into elementary sounds. Fourier's analysis, for example, makes great use of this property.

Somehow, our ear actually carries out a spectral analysis of the sounds it receives (this mechanism is illustrated in Physiology of the auditory system). Therefore, we can ask:

Given a sound that is the sum of two component sounds, can our ear always decompose it and distinguish its components?

In many cases, the answer is negative. For example:

1. when two simultaneous sounds have very similar pitches (see the page on beats).
2. when one of the two sounds is much louder than the other (simultaneous masking).
3. when a loud sound closely precedes a softer sound (forward time masking)
4. when a loud sound closely follows a softer sound (backward time masking)

What we have in all of these cases is a form of masking. Due to its structure, the ear cannot decompose a received sound into its physical components and perceives a single sound (as in cases 2, 3, and 4) or perceives a sound with completely different characteristics (as happens in the case of beats). The origin of the phenomenon can be explained by studying the physiology of the auditory system, and, in particular, through the concept of critical bands. We provide various examples below.

Simultaneous masking

Common experience tells us that it is more difficult to hear a sound clearly when background noise is present. This is made obvious by everyday experience; however, if we think about this again, it is actually a clear violation of the superposition principle. This is proof that the principle cannot be applied to perceived sounds.

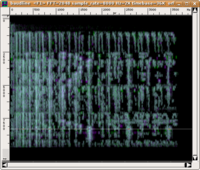
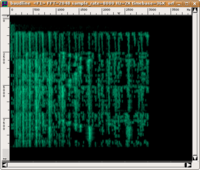
Here are two examples: in the first, a louder pure sound is masking a softer sound within the same critical band (from 400 to 510 Hz). In the second, white noise is demonstrated to be more effective in masking a pure sound. As a matter of fact, masking is achieved even if the white noise is filtered so that it does not contain spectral components in the same critical band as the pure sound.

	masch_sim.mp3 A pure sound with an amplitude of 0.95 at 500 Hz masking a sound with an amplitude of 0.1 (about 20 dBm less intense) at 440 Hz.
	masch_sim_rumore.mp3 White noise with the 400-500 Hz band suppressed masking a pure sound at 440 Hz.

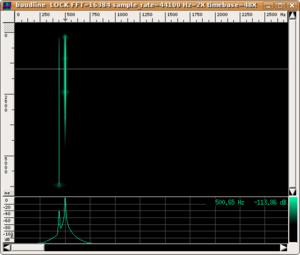
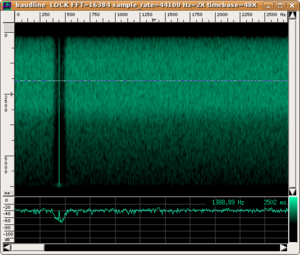
However, it is interesting to note that we can have an inverse phenomenon: if a group of people are sitting together at a table and are all speaking animatedly, our brain can filter out the background noise and focus on the particular conversation we are interested in. The same can be said for a table next to us, if a person were speaking badly about us in a low voice, we could clearly pick out their voice from the background noise. This is known as the cocktail party effect.

Paradoxically, it is also curious to note that if the superposition principle were not valid for physical sounds, we would not be able to distinguish any conversation at all within a group of people that were all speaking at the same time.

Time masking

This phenomenon happens when a weak sound follows, or even precedes, a louder sound. The weak sound is not perceptible if the time interval between the two sounds is below a particular threshold. For forward time masking, i.e. when the loud sound precedes the weak sound, the threshold is about 50 ms. For backward time masking, the threshold is about 10 ms.

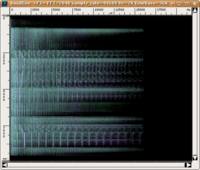
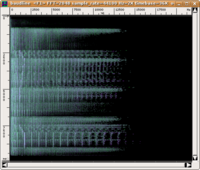
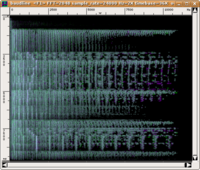
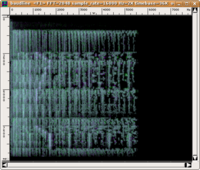
In the following example, a glissando from 200 to 3200 Hz is executed three times. In each case, as can be seen in the sonogram on the left, the sound is interrupted for 150 ms; however, the interruption is only perceptible in the third repetition. In the first repetition, the brief silence is masked by white noise, while in the second, it is masked by white noise from which the 900 to 2000 Hz band has been removed (this band would include the frequency of the glissando in the 150 ms in which it actually ceases).

Sonogram	Audio
	masch_temp.mp3 Time masking that gives the illusion of sound continuity

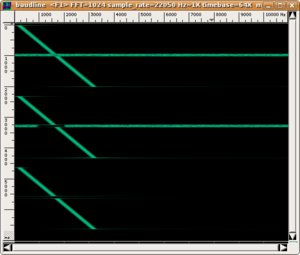
In-depth study and links

See the sections regarding:

• Critical bands
• Acoustic effects and illusions
• Physiology of the auditory system

For people who want to know more about the use of masking in the MP3 format, we highly recommend this excellent article Perceptual Coding: How MP3 Compression Works.

---