Enunciato del teorema di Fourier

Data una funzione ${\displaystyle y(t)}$

1. periodica di periodo T
2. limitata
3. integrabile in [0,T]

allora ${\displaystyle y(t)}$ è sviluppabile in serie di Fourier, cioè

${\displaystyle y(t)=a_{0}+\sum _{n=1}^{\infty }[a_{n}\cos(\omega _{n}t)+b_{n}\sin(\omega _{n}t)]}$

(1)

dove a_n e b_n sono opportuni coefficienti che dipendono dalla forma analitica della funzione periodica ${\displaystyle y(t)}$, e

${\displaystyle \omega _{n}={\frac {2\pi n}{T}}}$.

La sinusoide avente frequenza uguale alla frequenza fondamentale ${\displaystyle f_{0}}$ si dice anche armonica fondamentale o prima armonica; le sinusoidi aventi frequenza multipla della frequenza fondamentale si dicono armoniche successive (seconda, terza, ecc.) o anche parziali. Un'oscillazione (onda) costituita da più armoniche verrà detta onda complessa. Ogni onda complessa avrà un suo contenuto armonico caratterizzato dai diversi valori delle ampiezze e delle fasi delle varie armoniche in cui essa si scompone.

Calcolo dei coefficienti dello sviluppo di Fourier

Per il calcolo dei coefficienti ${\displaystyle a_{n}}$ e ${\displaystyle b_{n}}$ si tenga presente che:

• se la funzione ${\displaystyle y(t)}$ è dispari, come lo è la funzione seno, si otterrà una serie di soli seni (cioè i coefficienti ${\displaystyle a_{n}}$ sono tutti nulli);

• se la funzione ${\displaystyle y(t)}$ è pari, come lo è la funzione coseno, si otterrà una serie di soli coseni (cioè i coefficienti ${\displaystyle b_{n}}$ sono tutti nulli).

In generale i coefficienti si calcolano mediante i seguenti integrali:

${\displaystyle a_{0}={\frac {1}{T}}\int _{0}^{T}y(t)\,dt}$ che non è altro che il valor medio della funzione ${\displaystyle y(t)}$ sull'intervallo di periodicità [0,T].

${\displaystyle a_{n}={\frac {2}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}y(t)\cos(\omega _{n}t)dt}$

${\displaystyle b_{n}={\frac {2}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}y(t)\sin(\omega _{n}t)dt}$

Esempi di serie di Fourier

Presentiamo alcuni sviluppi notevoli che troverai utilizzati anche nel nostro laboratorio virtuale per la costruzione delle forme d'onda di default.

In seguito assumeremo sempre che:

• le forme d'onda abbiamo periodo T (la loro espressione analitica verrà data solo in un intervallo di periodicità che, per sfruttare le eventuali simmetrie della funzione, è stato "centrato" nell'origine, cioè andrà da -T/2 a T/2);

• il valore medio della funzione sia sempre nullo di modo che il coefficiente ${\displaystyle a_{0}}$ sia sempre nullo;

• l'ampiezza della funzione valga 1.

Onda triangolare

Con le assunzioni precedenti, l'onda triangolare può essere rappresentata in forma analitica dall'espressione

${\displaystyle y(t)={\begin{cases}{\frac {4}{T}}t&{\rm {se}}\quad -{\frac {T}{2}}\leq t<0\\-{\frac {4}{T}}t&{\rm {se}}\quad 0\leq t\leq {\frac {T}{2}}\end{cases}}}$

Poiché la funzione è pari, si otterrà una serie di soli coseni. Il calcolo degli integrali (2) e (3) conduce in effetti al risultato

${\displaystyle \,\!b_{n}=0}$

${\displaystyle a_{n}={\begin{cases}{\frac {8}{n^{2}\pi ^{2}}}&n\quad {\rm {dispari}}\\0&n\quad {\rm {pari}}\end{cases}}}$

Il risultato ottenuto mostra quindi che la serie è di soli coseni e che sono presenti solo armoniche dispari. Puoi verificare direttamente dall'applet (selezionando forme d'onda:triangolo) tali risultati:

• osserva che sono presenti solo armoniche dispari;
• passando con il mouse sulla paletta relativa ad ogni armonica puoi verificare che l'ampiezza per l'armonica n-esima è data proprio (salvo errori di arrotondamento) da

${\displaystyle a_{n}={\frac {8}{n^{2}\pi ^{2}}}}$

• che la fase di ogni armonica è nulla (l'applet lavora proprio con funzioni coseno)

funzione d'onda nel tempo	ampiezze delle componenti di Fourier (seno)

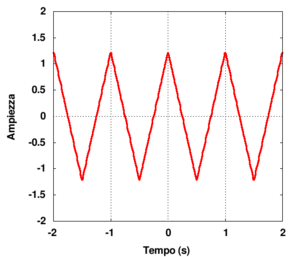
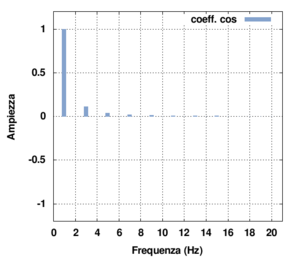
Onda quadra

Con le assunzioni precedenti, l'onda quadra può essere rappresentata in forma analitica dall'espressione

${\displaystyle y(t)={\begin{cases}-1&{\rm {se}}\quad -{\frac {T}{2}}\leq t<0\\1&{\rm {se}}\quad 0\leq t\leq {\frac {T}{2}}\end{cases}}}$

Poiché la funzione è dispari, si otterrà una serie di soli seni. Il calcolo degli integrali (2) e (3) conduce in effetti al risultato

${\displaystyle \,\!a_{n}=0}$

${\displaystyle b_{n}={\begin{cases}{\frac {4}{n\pi }}&n\quad {\rm {dispari}}\\0&n\quad {\rm {pari}}\end{cases}}}$

Il risultato ottenuto mostra quindi che la serie è di soli seni e che sono presenti solo armoniche dispari. Puoi verificare direttamente dall'applet (selezionando forme d'onda:Onda quadra) tali risultati:

• osserva che sono presenti solo armoniche dispari;
• andando con il mouse sulla paletta relativa ad ogni armonica puoi verificare che l'ampiezza per l'armonica n-esima è data proprio (salvo errori di arrotondamento) da

${\displaystyle a_{n}={\frac {4}{n\pi }}}$.

• È curioso osservare che l'ampiezza della fondamentale è maggiore dell'ampiezza dell'intera onda quadra;
• la fase di ogni armonica è pari a ${\displaystyle -{\frac {\pi }{2}}}$. Cio è corretto ricordando
  • che l'applet sviluppa in serie utiizzando solo funzioni coseno;
  • l'identità trigonometrica ${\displaystyle \cos \left(\alpha -{\frac {\pi }{2}}\right)=\sin(\alpha )}$

funzione d'onda nel tempo	ampiezze delle componenti di Fourier (coseno)

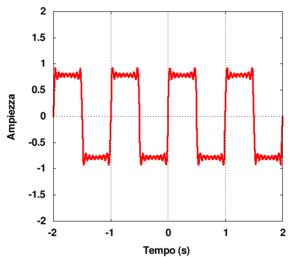
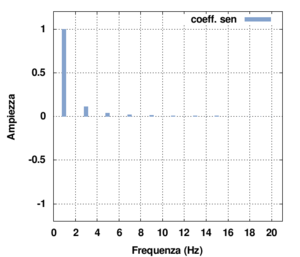
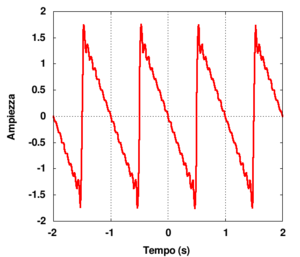
Onda a Dente di sega

Con le assunzioni precedenti, l'onda "a dente di sega" può essere rappresentata in forma analitica dall'espressione

${\displaystyle y(t)={\begin{cases}{\frac {2}{T}}t&{\rm {se}}\quad -{\frac {T}{2}}\leq t<{\frac {T}{2}}\end{cases}}}$

Poiché la funzione è dispari, si otterrà una serie di soli seni. Il calcolo degli integrali (2) e (3) conduce in effetti al risultato

${\displaystyle \,\!a_{n}=0}$

${\displaystyle b_{n}={\begin{cases}{\frac {2}{n\pi }}&n\quad {\rm {dispari}}\\-{\frac {2}{n\pi }}&n\quad {\rm {pari}}\end{cases}}}$

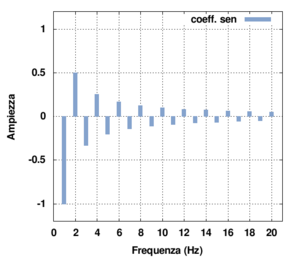
Il risultato ottenuto mostra quindi che la serie è di soli seni e che sono presenti solo armoniche dispari.

funzione d'onda nel tempo	ampiezze delle componenti di Fourier (seno)

Puoi verificare direttamente dall'applet (selezionando forme d'onda:Dente di sega) tali risultati:

• osserva che ora sono presenti tutte le armoniche;
• andando con il mouse sulla paletta relativa ad ogni armonica puoi verificare che l'ampiezza per l'armonica n-esima è data proprio (salvo errori di arrotondamento) da

${\displaystyle a_{n}={\frac {2}{n\pi }}}$.

• che la fase delle armoniche vale alternativamente a ${\displaystyle -{\frac {\pi }{2}}}$ e ${\displaystyle {\frac {\pi }{2}}}$ . Ciò è corretto ricordando
  • che l'applet sviluppa in serie utilizzando solo funzioni coseno;
  • l'identità trigonometrica

${\displaystyle \cos \left(\alpha -{\frac {\pi }{2}}\right)=\sin(\alpha )}$

${\displaystyle \cos \left(\alpha +{\frac {\pi }{2}}\right)=-\sin(\alpha )}$

Assumendo le ampiezze come positive, l'applet "scarica" il segno meno realtivo agli ${\displaystyle b_{n}}$ con n dispari, sulla fase dell'onda cosinusoidale.

---