Why use model instruments?

In physics, when we need to solve a difficult problem, we often adopt the following strategy: Let's solve a simpler problem first.

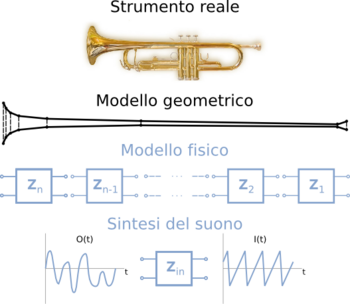
The study of the acoustic properties of a musical instrument is almost always a rather complex problem and must be solved with appropriate theories and experimental instruments. However, in some cases regarding particularly simple elements, it is possible to calculate analytical solutions to the wave equation and thus obtain interesting information. These elementary systems can then be combined together to obtain less simple geometries and are, therefore, the foundation for a more accurate analysis. Moreover, the fact that these solutions are also often conceptually as well as geometrically simple, model instruments allow our brain to truly understand the relevant physical phenomena both within and at the end of the tube.

A similar approach is also adopted in the analysis of vibrating systems, when we try to reduce them to a set of simple vibrating systems (see the pages on Harmonic motion, Normal modes and Resonance in buildings). The harmonic oscillator is the case with the simplest understanding and solution, however, it can often accurately describe the vibration of very complex structures, especially if it is in combination with other oscillators.

Even though these simple cases do not correspond exactly to any instrument of the orchestra, they are an ideal playground for our understanding of wave phenomena. In such cases, it is easier to solve the wave equation allowing us to visualise the solution and to obtain and discuss the primary acoustic properties of the system. Then, we could compare the properties of these "laboratory instruments" with those of real instruments to understand to what extent our model is accurate and what are the limits of its applicability.

Simplifying hypotheses

In a series of dedicated pages, we analyse the case of propagation of sound waves in bores of elementary geometry, such as cylindrical bores, conical bores and combinations of both. The primary simplifying hypothesis is to 'assume that waves propagate exclusively along the bore axis and not radially to it.

Bore with propagation:
Only along the axis	Also perpendicular to the axis

This hypothesis is physically justified when the section of a bore is not very large. In fact, considering the possible stationary waves that can be set transversally to a bore with a diameter of 1 cm, we can easily calculate that the lowest possible frequency is about 17 kHz (with regards to this, see Eigenfrequencies of bores). This frequency is at the limit of ultrasounds and, therefore, cannot have a great effect on the acoustic response of the bore. However, this hypothesis is quite realistic for instruments of small diameters, such as the flute. However, for a bore with a diameter of 5 cm, the frequency is as low as 6 kHz and the effect can no longer be ignored.

Other problems arise, for example, from an accurate description of the bells that form the mouth of brass instruments and contribute greatly to determining their characteristic voices. We will better discuss this and other problems, such as the effect of sound radiation from the open ends of a bore and the effect of friction, on their dedicated pages.

Method

As we fully discussed on the page dedicated to the Principle of superposition and as is evident viewing the table of Sound pressure levels, we know that sound waves produced by musical instruments are pressure waves corresponding to a very light perturbation with respect to the value of atmospheric pressure. In other words, sound waves are low amplitude waves, even for rather loud sounds within the limits of tolerability of the human ear. However, shock waves, such as in explosions, are quite different and we are not interested in them here (feel free to visit the page dedicated to the loudest possible sounds). For this reason, we can always study propagation in its linear approximation; i.e. assuming that the response of an element at the sum of two stimuli is none other than the sum of the responses of each of the two stimuli. This means that we can adopt the concept of impedance to describe the response of bores.

For a more detailed discussion of this concept, we suggest you read the pages on Impedance, Acoustical impedance, Impedance matching, Sound and resonance and their links. Here, we remind you that incoming impedance in a bore is a property of the bore (therefore, independent of how it is excited), which for each frequency f indicates the ratio between the values of sound pressure at the mouth of the bore and the incoming air flow and their phase difference.

${\displaystyle Z(f)={\frac {p(f)}{U(f)}}}$.

The unit of measurement used is the acoustic ohm, which corresponds to an acoustic pressure of 0.1 Pa over a volume velocity of 1 cm³ per second (si veda Impedance and Pressure and its units of measurement).

Thanks to the principle of superposition, impedance can be calculated separately for each frequency by exciting a bore with a pure sinusoidal signal, while the response to a more complex periodic signal is obtained by combining the responses of the various frequencies contained in the composite signal (as obtained by applying Fourier's theorem). To see several examples of decompositions of complex signals in sinusoids, visit the pages on Fourier's theorem and Fourier series expansions.

The magnitude of the impedance of sound tubes is a property that is always characterised by the presence of deep maxima and minima; a fact clearly indicating that tubes are narrowband resonators. In other words, they are able to quench all frequencies except the eigenfrequencies of the system (visit the pages on Resonance, Normal modes, Eigenfrequencies and Eigenfrequencies of bores). Our primary interest on these pages is to understand how these resonance frequencies are distributed, as many characteristics of sounds emitted from bores depend on this fact (see Perception of timbre).

Links

The pages are organised in the following manner:

• Cylindrical bore: we examine the well known properties of the ideal cylindrical bore (e.g. see Eigenfrequencies of bores) from the point of view of the concept of impedance. We also examine the case of less ideal bores.
• Modified cylindrical bore: we study the effect of enlarging or shrinking a portion of a cylindrical bore. We also study the effect of coupling of bores (or waveguides) with Helmholtz resonators (or resonance in enclosures).
• Conical bore: the response of the conical bore and cylindrical bore are compared and an apparent paradox is discussed.
• Mixed bore: cylindrical and conical elements are combined simply to study how the response changes.
• Refraction in bores: does not regard bores similar to those that compose real musical instruments but is an alternative illustration of the concepts of Reflection, Refraction and Impedance matching.

---