Che cos'è e a che cosa serve la funzione d'onda

• La funzione d'onda è una funzione matematica ${\displaystyle \psi }$ utilizzata per descrivere un'onda. Essa contiene tutte le informazioni riguardanti la grandezza che oscilla.
• Il significato fisico e le unità di misura di ${\displaystyle \psi }$ variano a seconda della natura dell'onda stessa.
• Alcuni esempi:

tipo di onda	grandezza descritta dalla funzione d'onda
onde elettromagnetiche	campo elettrico, o campo magnetico
onde del mare	livello dell'acqua rispetto al mare calmo
onde sonore	pressione (o spostamento) dell'aria rispetto all'aria in quiete
onde elastiche	deformazione del mezzo

Nota Bene: la funzione d'onda contiene informazioni dirette sulla grandezza che oscilla, e non sul mezzo che eventualmente supporta l'oscillazione. Per esempio, nel caso delle onde del mare, ${\displaystyle \psi }$ descrive il profilo della superficie, ma non contiene direttamente informazioni sull'acqua. Tuttavia lo studio della propagazione delle onde in un mezzo spesso fornisce informazioni sulla natura del mezzo. Per esempio:

• misurare il cambiamento di direzione di un'onda luminosa quando passa dall'aria al vetro ci dice il valore dell'indice di rifrazione del vetro rispetto a quello dell'aria (si veda la sezione rifrazione).
• osservare come un'onda viene riflessa o trasmessa all'interfaccia tra due sostanze diverse indica direttamente quanto le sostanze si oppongono alla trasmissione di energia per mezzo dell'onda stessa (si veda la sezione rifrazione nelle corde)
• misurare le proprietà delle onde sismiche quali ampiezza, direzione di oscillazione, tempi di arrivo al sismografo non solo indica dove si trova l'epicentro di un terremoto, ma può dare preziose informazioni riguardo alla struttura interna della terra (si veda la sezione velocità delle onde meccaniche).
• la maggior parte delle proprietà della materia al livello molecolare o atomico sono misurate irraggiando un campione con onde (in genere elettromagnetiche come luce visibile, ultravioletta, raggi X, raggi ${\displaystyle \gamma }$, ma anche fasci di elettroni o neutroni), ed osservando la reazione del campione

Nelle sezioni successive esaminiamo alcune proprietà della funzione d'onda indipendenti dal tipo di onda a cui essa si riferisce.

Il caso generale: le onde viaggianti

Abbiamo detto che ${\displaystyle \psi }$ è chiamata "funzione" d'onda. Una funzione è una corrispondenza tra variabili. Quali sono queste variabili? Sappiamo che la natura di ${\displaystyle \psi }$ dipende dal tipo di onda che essa descrive, ma le variabili indipendenti sono, nella maggioranza dei casi, sempre le stesse: sono le coordinate nello spazio e nel tempo.

Esaminiamo dapprima il caso di onde che si propagano in una sola dimensione x.

• In generale la grandezza descritta dalla funzione d'onda varia nello spazio e nel tempo, perciò ${\displaystyle \psi }$ deve essere funzione della posizione x e del tempo t.

${\displaystyle \psi (x,t)\!}$.

• In tre dimensioni, al posto della coordinata x dovremo usare il vettore posizione r

${\displaystyle \psi (\mathbf {r} ,t)}$.

• Se il mezzo in cui si propaga l'onda è a sua volta in movimento il vettore posizione potrà a sua volta dipendere dal tempo

${\displaystyle \psi (\mathbf {r} (t),t)}$.

Il caso più comune: onde che si propagano senza cambiamento di forma

Ora assumiamo che l'onda abbia la proprietà che il suo profilo non cambi durante la propagazione. Ciò significa che, anche se il disturbo dell'onda si trasmette nello spazio, la sua forma non cambia. Per inciso, questa proprietà, che non è affatto comune a tutti i modi e i mezzi di propagazione, è molto importante per l'utilizzo delle onde nelle telecomunicazioni. Infatti possiamo codificare nella forma d'onda che trasmettiamo un segnale, ma che ne è del nostro segnale se la forma d'onda è cambiata, quando l'onda giunge a destinazione?

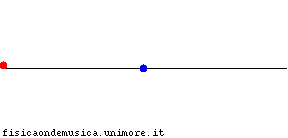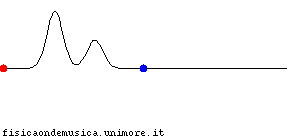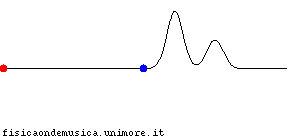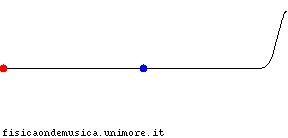
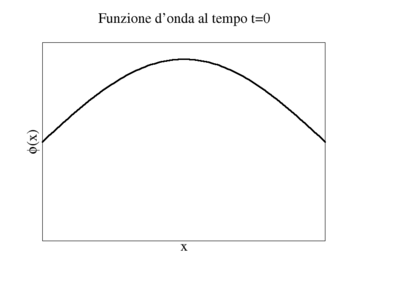
Per trovare l'espressione matematica di un'onda la cui forma non cambia durante la propagazione ragioniamo così:

Al tempo t=0 possiamo scattare una fotografia dell'onda: avremo la funzione ψ(x,0).	Aspettiamo un tempo Δt, e scattiamo un'altra fotografia. Avremo la funzione ψ(x, Δt).

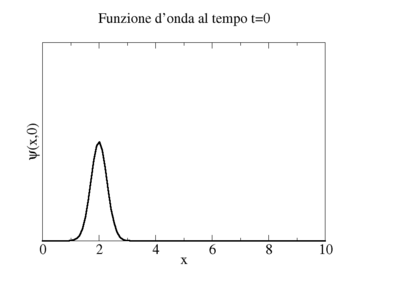
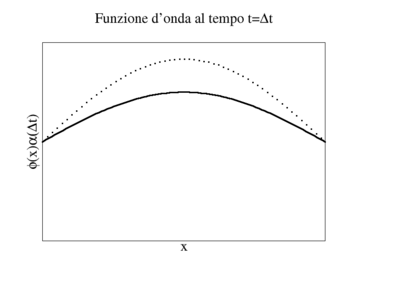
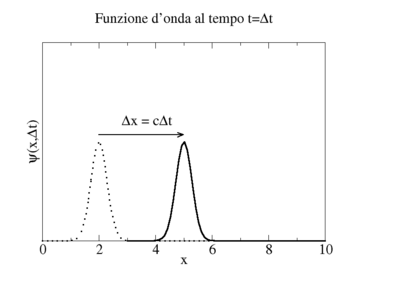
Ora, se la seconda fotografia altro non è che una traslazione della prima, cioè uno spostamento lungo l'asse x senza che la forma della funzione sia cambiata, dovrà essere

${\displaystyle \psi (x,\Delta t)=\psi (x-\Delta x,0)\!}$.

La funzione ${\displaystyle \psi }$ è rimasta la stessa, ma il suo profilo è spostato a sinistra lungo l'asse x di un tratto ${\displaystyle \Delta x}$

• Se sappiamo che la velocità di traslazione è c, allora possiamo mettere in relazione tra loro lo spostamento del profilo nello spazio (${\displaystyle \Delta x}$) con il tempo intercorso tra le due fotografie (${\displaystyle \Delta t}$)

${\displaystyle \Delta x=c\Delta t\!}$,

e, di conseguenza, possiamo ottenere l'espressione della funzione d'onda per tutti i tempi che vogliamo:

${\displaystyle \psi (x,t)=\psi (x-ct)\!}$.

Il secondo caso più comune: oscillazioni senza propagazione

La forma generale della funzione d'onda sopra ricavata è appropriata per tutte le onde, ma descrive un disturbo che si sposta nello spazio con velocità c. Qual è l'espressione matematica della funzione d'onda ${\displaystyle \psi }$ se essa descrive un'oscillazione, ma non una propagazione da un punto all'altro? (la sezione modi normali illustra l'importanza di questo caso, e contiene diversi esempi di questo tipo di oscillazioni)

In questo caso possiamo ragionare come segue:

Scattiamo una fotografia al tempo ${\displaystyle t=0}$, ed avremo un certo profilo ${\displaystyle \psi (x,0)=\phi (x)\!}$	Dopo un tempo ${\displaystyle t}$ il profilo ${\displaystyle \phi }$ dell'onda non si è spostato, come nel caso delle onde viaggianti, ma è rimasto dov'era. Tuttavia esso è modificato per un fattore moltiplicativo ${\displaystyle \alpha }$ che dipende solo dal tempo t. ${\displaystyle \psi (x,t)=\phi (x)\alpha (t)\!}$

In questa forma, che descrive le onde senza propagazione, o stazionarie, si nota che le variabili spazio e tempo sono separate ciascuna in una differente funzione: ${\displaystyle \phi \!}$ per lo spazio, e ${\displaystyle \alpha \!}$ per il tempo. Questo fatto costituisce una semplificazione notevole per la soluzione dell'equazione delle onde.

Si noti che il termine stazionario non significa affatto che la funzione d'onda non dipende dal tempo, ma indica il fatto che la posizione dei punti per cui la funzione d'onda è nulla (detti nodi) non cambia nel tempo . Infatti, se, per un certo punto ${\displaystyle x_{0}}$, all'istante iniziale ${\displaystyle t=0}$ si ha che

${\displaystyle \phi (x_{0})=0\!}$,

allora, anche per un qualunque istante successivo t si ha

${\displaystyle \psi (x_{0},t)=\phi (x_{0})\alpha (t)=0\!}$,

cioè la posizione del nodo non cambia nel tempo.

Onde sferiche

Ogni volta che un'onda possiede una particolare simmetria, questa simmetria si riflette sulla sua espressione matematica.

Per esempio, sappiamo che un'onda ha simmetria sferica quando il suo profilo ${\displaystyle \psi }$ non dipende dall'angolo da cui lo si guarda. Potremmo anche dire che, se ruotiamo il sistema di coordinate, il profilo non varia.

È evidente che l'espressione

${\displaystyle \psi (\mathbf {r} ,t)\!}$

descrive ancora l'onda sferica, ma è anche chiaro che essa potrebbe essere di molto semplificata. Infatti, vediamo che se ruotiamo le coordinate ${\displaystyle \mathbf {r} \to \mathbf {r'} }$, la precedente espressione cambia, non rendendo evidente, così, la simmetria.

Da quale variabile allora può dipendere ${\displaystyle \psi }$, oltre che dal tempo?

Deve trattarsi di una variabile che non cambia se ruotiamo le coordinate. Questo è il caso, ad esempio, della distanza da un certo punto (che può essere semplicemente l'origine delle coordinate). Detta r questa distanza

${\displaystyle r=|\mathbf {r} |}$

l'onda sferica è convenientemente espressa nella forma

${\displaystyle \psi (r,t)\!}$.

Se ora effettuiamo una rotazione delle coordinate ${\displaystyle \mathbf {r} \to \mathbf {r'} }$, l'espressione resta invariata, perché la distanza r resta invariata ${\displaystyle r'=|\mathbf {r'} |=|\mathbf {r} |=r}$.

Possiamo andare oltre se ci riferiamo ad un particolare tipo di propagazione: quella che avviene senza variazione di energia.

---